连续扫描法不同取点方式采集曲线曲面数据的误差研究

黄锦文

（江西冶金职业技术学院，江西 新余338015）

1 引 言

在逆向工程中，三坐标测量机CMM 已经普遍用于测量曲线曲面。CMM 测量数据的方式，分为点位式和连续扫描式［1］。点位式通常用来对经过分布规划的已知方程曲线曲面进行测量，测量效率比较低［2］。连续扫描测量通常用来对未知曲面方程曲线曲面进行测量。计算机根据离散点采用拟合方法构建出曲线曲面，拟合包括插值和逼近［3］。因为取出的数据点有限，计算机构建出来的曲线曲面和理论曲线曲面之间有误差。扫描过程中要研究如何取出数据点，在数据点数量尽量少的情况下，使计算机构建出来的曲线曲面误差最小，即如何在连续截面扫描中，通过合理的取点方式实现自适应采样。本文对一给定的理论曲线以不同取点方式采集出相同数量的点。然后，利用MATLAB 进行数据点拟合，计算在相同x 处拟合曲线和理论曲线差值，给出误差分布图。分析误差分布图，得出等角度变化和法可以实现数据点的自适应分布。

2 理论曲线

图1 函数y=sinx 图

研究曲线方程为y=sinx（x∈［0，π］）（1）

然后，求解相同点处（xk，yk）的误差e（yk）

最后给出分布图，并进行分析。

3 不同取点方式

3.1 等Δx 法

等Δx 法，就是取出点（xj，yj|j=1，…m；m=21）把x 轴分成20 均匀等分xj+1-xj=π/20，x1=0，xm=π。在这些点中，插值出一组新的点（xk，yk），并 计 算 误 差e（yk）。最后给出误差分布图2（x，e（y）），这些取出点的分布如图3所示。

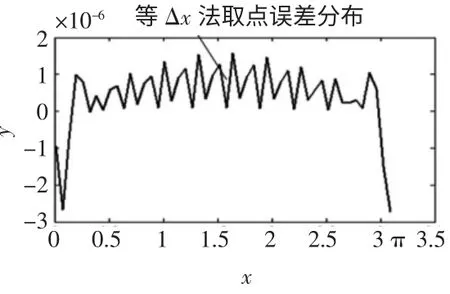
图2 等Δx 法误差分布

图3 等Δx 法取点在曲线上的分布图

3.2 等弦长法

取出的21 个点中相邻两点（xj，yj）和（xj+1，yj+1）之间的距离dj为弦长值，

等弦长法就是使所有的dj相等，在这些点中，插值出一组新的点（xk，yk），计算误差e（yk），给出误差分布图4（x，e（y）），这些取出点的分布如图5 所示。

3.3 等弧长法

图4 等弦长法误差分布

图5 等弦长法取点的分布图

弧长法就是在取出的21 个点中，相邻两点（xj，yj）和（xj+1，yj+1）之间的弧长Sj相等。弧长的算法可以近似地按照下面的式子进行

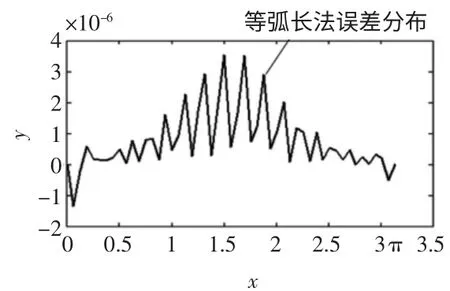
图6 等弧长法误差分布图

式中，di是离散出的数据点中相邻两点（xi，yi）和（xi+1，yi+1）之间的距离，Lj和Uj分别是取出点中第j 点（xj，yj）和j+1 点（xj+1，yj+1）对应离散样本数据点（xi，yi）的位置（即i=Lj和i=Uj，Uj>Lj）。同样，得到误差分布图6 和取出点的分布图7。

3.4 等角度变化和法

图7 等弧长法取点在曲线上的分布

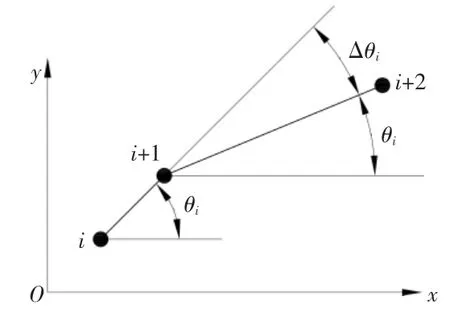
图8 离散样本点中相邻三点角度关系

（等积分角度法）

如图8 所示，离散样本点中相邻三点（第i、i+1、i+2 个点），第i 个点和第i+1 个点之间的连线与x 轴所成角度θi，第i+1 个点和第i+2 个点之间的连线与x 轴所成的锐角为θi+1，两者之间变化绝对值为：

θi可以通过以下两个式子来计算得到

角度变化和为Qj为

图9 等角度变化和法的误差图

图10 等角度变化和法的取点分布

等角度变化和法取点就当Qj值达到一定值就取点的一种数据采集方式。式（9）中，Lj和Uj分别是取出点中第j点（xj，yj）和j+1 点（xj+1，yj+1）对应离散样本数据点（xi，yi）的位置（即i=Lj和i=Uj，Uj>Lj）。图9 为该方法得到的误差分布图，取出点的分布如图10。

比较四幅误差图2、4、6、9 可知，等角度变化和法误差值随曲率增大而减小，而其他几种方法在曲率值较大处的误差值也大。等角度变化和法误差值在曲率较小处相对于其他几种取点方式要大，原因是在曲率值较小处数据采集点比较稀，如图10 所示。从图9 还可以确定，对曲率越大或曲率变化越大的未知复杂曲面进行扫描测量，等角度变化和取点法可以实现在尽量少的点数情况下尽可能地反映曲线曲面，即实现自适应采样。

［1］ 金涛，童水光.逆向工程技术［M］.北京：机械工业出版社，2003.

［2］ 张国雄.三坐标测量机［M］.天津：天津大学出版社，1999.

［3］ 郑咸义.计算方法［M］.广州：华南理工大学出版社，2003.