聚丙烯反应器熔融指数预测控制算法
王天培, 翟春艳, 刘慧哲, 李书臣, 苏成利
(辽宁石油化工大学,辽宁抚顺113001)
聚丙烯(PP)在热塑料材料产品中占据着重要的地位,在化工生产中聚丙烯也是极其重要的原材料和产品。熔融指数(MI)可以表征聚丙烯在熔融状态下的黏流特性,对聚丙烯及其制品的质量有很大的影响[1]。从实验室离线化验分析得到聚丙烯熔融指数,由于滞后时间较长,不能达到生产实时控制的要求[2]。所以实现熔融指数的软测量以及牌号切换过程的预测控制对整个工业聚合过程有重要意义。
目前,国内外很少采用机理建模法进行数学建模,针对环管反应器聚丙烯的熔融指数都是从反应机理的角度进行理论分析与研究。在环管反应工艺中,徐用 懋等[3-5]根据BWR 方 程 和 亨 利 定 律 建 立 了丙烯聚合的机理模型。K BMcAuley[6]在建立熔融指数模型时,充分考虑了影响共聚反应的多种因素,把共聚单体、氢气、助催化剂和杂质与单体浓度比以及反应温度等参数加入物理模型当中,由于影响参数比较多,调整起来较为缓慢。金学兰等[7-8]对McAuley的模型参数进行了调整和改进,用宏观反应热替换了反应温度,使模型更为精确。田华阁等[9]在金学兰的模型基础上,建立了两种双环管反应器的机理模型,不仅模型的信息完整,而且适用于实际工业生产。
在双环管反应器中,熔融指数的累积值与瞬时值可以由微分方程表示。聚丙烯的牌号切换过程就可以用非线性Hammerstein 模型来表示。文献[10]虽然对Hammerstein非线性系统提出了预测控制策略,但计算量较大,控制精度不高。何德峰等[11]利用黎卡提方程构造控制函数,但计算机实现较为复杂。王平等[12]将牌号切换优化控制归结为非线性动态优化问题再滚动求解,但预测性能不佳。
本文采用金学兰、田华阁等人的熔融指数模型,建立了熔融指数的累积模型。利用建立好的熔融指数模型和熔融指数累积模型转化为Hammerstein模型,并作为预测模型,实现聚合反应器熔融指数的预测控制,最后结合工艺实际装置对所建的控制系统进行仿真。
1 熔融指数软测量建模
熔融指数的机理建模通常从机理出发,建立聚合物的分子质量和其黏度的关系。由于聚合反应机理比较复杂,在考虑反应单体及氢气的浓度比等参数同时,将宏观反应热Hr替换聚合反应温度。考虑到对聚合速率的影响,本文采用以下熔融指数混合模型[7]:

其中MIi为环管反应器内熔融指数瞬时值,a0~a3为 待辨识系数,cH2/cM为 氢 气 与 丙 烯 量 浓 度 比,cp/cM为催化剂与丙烯量浓度比,Hr为宏观反应热。由于第一环管与第二环管的熔融指数具有一定的关系,在实际的生产中,只对第二反应管的熔融指数进行离线分析。故采用文献[9]的双环管混合模型:

其中MIi为第二环管反应器出口熔融指数瞬时值,b0~b5为待辨识系数。(cH2/cM)i(i=1,2)为第i个环管内氢气与丙烯量浓度比,(cp/cM)i(i=1,2)为第i 个环管内催化剂与丙烯量浓度比,Hr为宏观反应热。
双环管反应器出口的累积熔融指数的动态方程如下:
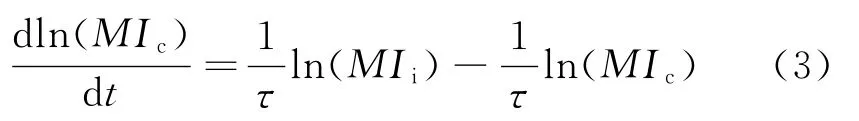
式中,MIc为累积熔融指数,MIi为瞬时熔融指数,τ为物料在环管反应器内停留的平均时间。
根据工艺流程,为得到稳定的熔融指数,对第二环管反应器的氢气浓度进行调节。氢气浓度变化导致瞬时熔融指数的对数即ln(MIi)发生变化,最后使累积熔融指数发生改变。设第二环管反应器氢气量浓度cH2为实际控制变量u(t),令y(t)=ln(MIc),v(t)=ln(MIi)=f(u(t)),为了便于计算机实现,将式(3)用差分方程的形式表示,即:

这样式(2)和式(4)就组成一个单输入/单输出的Hammerstein 模型。离散化的u(t)作为模型非线性部分的输入,v(k)作为模型的动态部分的输入,模型输出为y(k)。将这个H 模型作为预测控制的预测模型。累计熔融指数差分方程作为动态线性部分,式(2)作为静态非线性部分。通过设计H模型的预测控制器实现对牌号切换过程的闭环预测控制。
2 基于软测量模型的预测控制
针对有动态线性和静态非线性两部分的熔融指数模型,在其转化为Hammerstein模型后,借助于预测控制两步走思想,对其实现预测控制[13]。熔融指数模型的动态线性部分,可以设计出基于非线性H 模型广义预测控制算法,从而先求得输出预测控制所需的中间控制变量;再利用中间控制变量,通过静态非线性模型求解实际控制变量。
针对其中的线性部分设计广义预测控制,预测控制系统结构如图1所示。

图1 预测控制系统结构Fig.1 The system structure of predictive control
为实现广义预测控制,先将式(4)的差分方程转换为受控自回归积分滑动平均模型(CARIMA)[14],即

式中,y(k)是熔融指数的输出,v(k)为中间变量,ξ(k)为白噪声序列,差分算子Δ=1-z-1;

为了实现系统的最优控制,采用对输出误差和控制增量加权的二次性能指标,如(8)式所示:

其中w(k+j)=αjy(k)+(1-αj)ysp(j=1,2,…,n),ysp为参考设定值,y(k)为输出,α 为柔化系数。Δv(k)是中间控制增量。P 为预测长度,M 为控制步长(M <P)。λ 为权系数,w(k+j)是模型预测输出值,^y(k+j)为输出预测值。
根据Diophantine方程

其中,Ej(z-1)=e0+e1z-1+e2z-2+…+ej-1z-j+1;Fj(z-1)=fj,0+fj,1z-1+fj,2z-2+…+fj,nAz-nA;Gj(z-1)=g0+g1z-1+…+gnB+j-1z-nB-j+1
则系统的输出预测表达式为:

式中,F(k)=H(z-1)Δv(k-1)+F(z-1)y(k);

对(8)式的控制增量Δv(k)求导,可推出最优控制律为:

式中,W(k+1)=[w(k+1)w(k+2)…w(k+P)]T。
在控制过程中,只将增量的第一个分量加入系统,

式中,dT=[GTG+λ]-1GT[1 0…0]T。
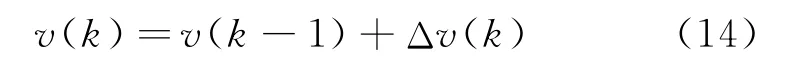
将参考轨迹W(k+1),H(z-1),F(z-1),代入式(12),计算出中间变量的增量ΔV(k);求解出ΔV(k)后,再由式(13)和(14)计算出v(k)。v(k)是一个不可测的中间变量,而不是一个实际的物理量,真正的控制变量u(k)是氢气的浓度cH2,描述了u(k)与v(k)的关系满足式(2)。u(k)的实际控制量是氢气浓度cH2,通过求解公式(2)的反函数,如式(15)所示,即可求出该控制量的值,将求出的u(k)作用于系统。

3 仿真分析
本文仿真对象选取双环管反应器的熔融指数模型[12],参考的辨识参数[15]如表1所示。

表1 式(2)的辨识结果Table 1 Identified results of equation(2)
取离散时间为0.5h,聚合物停留时间τ=2h,经过参数辨识,牌号切换过程可以用下面的模型来描述:

由式(13)和式(14)求解出v(k),再由式(15)求解出实际控制变量u(k)。为了验证本文预测控制算法的有效性,针对号牌切换的过程进行仿真,将氢气浓度作为调节变量,牌号规格参考文献[11]。预测控制模型参数如下:整个仿真时长为600个采样时间,预测长度P 为8,控制步长M 为2,柔化系数取0.7。以聚合物的质量偏差和控制变量的偏差的±5%作为合格的标准,在过程输出中加入均值为0,方差为0.01的噪声。先后给出3个不同的输出设定值,牌号A 到牌号B的动态过程如图2所示。

图2 牌号切换过程Fig.2 Grade transition process
从图2中可以看出,在牌号由A 切换到B 时,本文中提出的基于软测量Hammerstein 模型的广义预测控制算法,能够良好地跟踪设定值曲线,控制过程平稳。基于Hammerstein 模型的广义预测控制比NMPC算法[11]控制调节时间短,响应迅速,输出过程超调量小。
4 结论
以聚丙烯熔融指数的号牌切换为研究背景,选择了速度快外推性能好的机理模型作为熔融指数的软测量模型,根据熔融指数的累积特性,提出了累计熔融指数模型,并且与熔融指数模型一同以Hammerstein模型的形式作为预测控制的预测模型。针对多输入单输出的Hammerstein 系统,采用两步法求解预测控制的最优控制规律。实现聚合反应器熔融指数的预测控制。最后在聚丙烯牌号切换过程的控制仿真中,表现出跟踪性能好,牌号切换过程迅速等优点;验证了模型和算法的有效性和实用性。本文控制方法与其他控制算法相比,不仅缩短了切换时间,控制过程也较为平稳。在提高产品质量,增加物料利用率,减少废料的产出,节约能源等方面,对聚丙烯的工业生产有着重要的指导意义。
[1] 闫正兵,刘兴高,吴俊.丙烯聚合健康监控系统是优化生产过程研究[J].石油化工高等学校学报,2007,20(3):78-81.
[2] 楼巍,刘兴高.基于PCA-GA-RBF网络的聚丙烯熔融指数预报模型[J].石油化工高等学校学报,2007,20(3):82-85.
[3] 韦建利,范顺杰,徐用懋.聚丙烯牌号切换动态过程建模及仿真研究[J].系统仿真学报,2001,13(s1):140-142.
[4] 怀改平,徐用懋.气相丙烯聚合稳态模型的研究和仿真[J].计算机工程与应用,2004,40(21):203-209.
[5] 范顺杰,徐用懋.聚丙烯反应器的动态模拟[J].化工自动化及仪表,2000,27(5):5-8.
[6] McAuley K B,MacGregor J F.On-line inference of polymer properties in an industrial polyethylene reactor[J].AiChE J.1991,37(6):825-835.
[7] 金学兰,袁璞,胡品慧,等.丙烯聚合反应动态建模及在牌号切换中的应用[J].系统仿真学报,2006,18(8):2089-2092.
[8] 金学兰,袁璞,胡品慧,等.丙烯聚合反应动态模拟[J].化工自动化及仪表,2005,32(3):7-10.
[9] 田华阁,车荣杰,田学民.聚丙烯双环管反应器熔融指数机理建模[J].控制工程,2010,17(2):193-196.
[10] Rloemen H H J,Boom van de T J J,Verbruggen H B.Model-based predictive control for Hammerstein-wiener systems[J].International Journal of Control,2001,74(5):482-495.
[11] 何德峰,俞立.约束Hammerstein系统非线性预测控制及在聚丙烯牌号切换中的仿真研究[J].自动化学报,2009,35(12):1558-1563.
[12] 王平,田学民,黄德先.双环管聚丙烯反应过程牌号切换优化控制策略[J].清华大学学报,2012,52(9):1236-1243.
[13] 黄道平,朱学峰,周其节.基于一种集成模型的多变量非线性预测控制[J].控制理论与应用,1999,16(1):38-42.
[14] 高承武,侯立刚,李会举,等.基于差分算法的预测控制[J].辽宁石油化工大学学报,2009,22(3):62-64.
[15] 车荣杰.聚丙烯熔融指数软测量方法研究[D].青岛:中石油大学(华东),2009.

