我国房价与地价关系的实证分析

陈晓川，杨海艳

(福建师范大学 闽南科技学院，福建 泉州362332)

房价与地价的关系受到社会各界的普遍关注，究竟是房价推动地价上涨，还是地价带动房价攀升，这一问题已成为政府、房地产开发商和学术界争论的焦点。如建设部政策研究中心课题组认为地价上涨推动、房地产供给结构变动和多种住房需求旺盛是当前我国房价上涨的三大原因;国土资源部副部长、国家土地副总督察鹿心社在国新办新闻发布会上表示，我国不同类型房地产项目的地价占房价的平均比例为23.2%，决定房价的关键因素或者根本因素是供求关系;华远集团总裁任志强认为调控房价首先要抑制地价。因此，研究房价与地价的关系具有重要的现实意义。

1 文献综述

关于房价与地价的关系，国外学者进行了深入的分析。MUTH 通过构建空间竞价函数，认为高地价是由高房价引起的。DICKS 在研究英国的地价和存量住房价格后，认为在土地供给受限的房地产市场中，不应忽略地价对房价的影响［1］。ALYOUSHA 利用英格兰1981—1994 年间的季度数据对房价与地价的关系进行Granger 因果检验，结论表明，从长期看，房价变化会导致地价变化［2］。CHEN 认为地价和房价的波动趋势基本一致，分析房价的影响因素时可忽略地价的作用［3］。

除了国外学者的分析，国内学者也进行了一系列的研究。高波、毛丰付利用1999—2002 年间的季度数据对房价与地价关系进行Granger 因果检验和回归分析，认为长期内房价决定地价，短期内两者相互影响［4］。况伟大认为短期内房价和地价相互影响，长期内地价是房价的Granger 成因［5］。宋勃、高波则认为，就短期而言，房价对地价没有影响，而地价是房价的Granger 成因［6］;长期而言，房价和地价存在双向因果关系。王岳龙、张瑜证实了在全国范围内，无论是长期还是短期，房价都是地价的Granger 成因，而地价只是房价长期的Granger 成因［7］。陈会广、刘忠原认为短期内房价与地价互为影响，长期内房价是地价的Granger 成因，而不是相反［8］。

综上所述，学术界对房价与地价的关系进行了大量研究，但研究结论各异［9］。究其原因，一是样本容量受限，实证检验偏差较大;二是数据调整存在缺陷。笔者的研究将利用最新的季度数据和新的数据调整方法，运用协整检验和Granger因果检验探寻房价与地价的关系。

2 数据说明与技术路线

2.1 数据说明

考虑数据的可获取性，选取了1999 年第1 季度至2009 年第4 季度间的季度数据进行实证分析，样本容量为44，数据全部来源于国家统计局网站。选取的指标有全国房屋销售价格指数和土地交易价格指数，以全国房屋销售价格指数代表房价(HPI)，以土地交易价格指数代表地价(LPI)，由于房价指数和地价指数皆为同比指数(以上年同季为100)，因此有必要对同比指数进行调整。调整方法为:以1998 年各季指数为定基(100)，用HPAI 表示调整后的房屋销售价格定比指数，以LPAI 表示调整后的土地交易价格定比指数，则HPAIt/n=HPIt/n×HPAI(t－1)/n/100，LPAIt/n=LPIt/n× LPAI(t－1)/n/100，其中，t/n 表示年份/季度，t 为1999—2009 年，n 取值为1 ～4。调整后的定比指数既可以消除不同量纲的影响，又可以反映总体的增长性。调整后的数据如图1 所示。

图1 LPAI 和HPAI 趋势图

从图1 中可以看出，全国房价指数和地价指数总体上呈现波浪式上升趋势，带有常数和明显的时间趋势，且从2002 年第4 季度开始，全国地价指数均大于房价指数，说明从2002 年第4 季度开始我国地价增长速度快于房价增长速度。

2.2 技术路线

Granger 因果检验是考察两变量是否存在因果关系的常用方法，在考察序列X 是否是序列Y产生的原因时，其研究思路是:根据Y 的过去值(滞后期取值)对Y 进行自回归时，如果再加上X的过去值(滞后期取值)能显著增加回归的解释能力，则称X 是Y 的格兰杰成因，此时X 的滞后期系数具有统计显著性。利用同样的方法，可以考察序列Y 是否是序列X 的格兰杰成因。其检验模型为:

yt=α0+α1yt－1+…+αkyt－k+β1xt－1+…+βkxt－k+εt

xt=α0+α1xt－1+…+αkxt－k+β1yt－1+…+βkyt－k+εt

其中，k 为最大滞后阶数，通常可以取稍大一些。如果序列X(Y)是序列Y(X)的格兰杰成因，滞后阶数k 也可以作为考察作用的周期。

检验的原假设是序列X(Y)不是序列Y(X)的格兰杰成因，即β1=β2=…=βk=0。

检验统计量为F 统计量，如果计算出的F 统计量值超过给定显著性水平下的相应临界值，则应拒绝原假设，即认为序列X(Y)是序列Y(X)的格兰杰成因。

同时，根据GRANGER 提出的两变量因果检验只有在协整的情况下才有效。而在进行协整检验前，必须先对变量进行平稳性检验。因此，在具体检验过程中采用的技术路线是:①先对LPAI 和HPAI 进行平稳性检验，判断两者是否存在同阶单整;②如果存在同阶单整，就进行协整检验，判断两者是否存在协整关系;③如果存在协整关系，就进行Granger 因果检验，从而判断两变量的因果关系。

3 房价与地价关系的实证分析

3.1 LPAI 和HPAI 两变量平稳性检验

采用ADF(augmented dickey fulle)单位根检验的方法检验变量的平稳性，软件版本为EViews5.0。如图1 所示，LPAI 和HPAI 两变量变化具有明显的常数和时间趋势，因此检验类型选择含有常数项和趋势项。由AIC 和SC 的值确定最佳滞后期，具体检验结果如表1 所示。

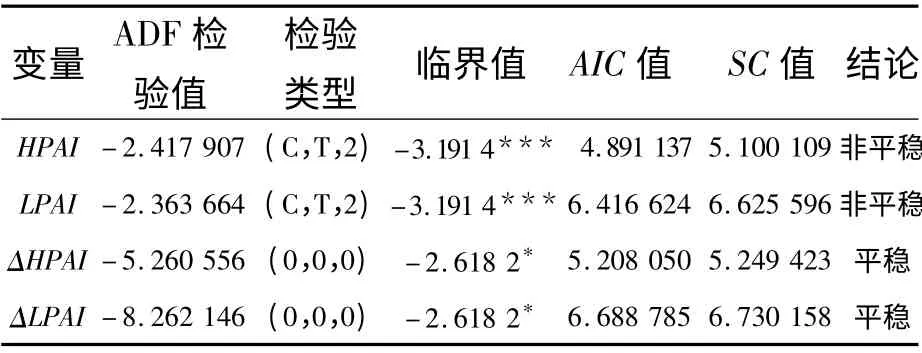
表1 HPAI 和LPAI 的单位根ADF 检验结果

由表1 可知，LPAI 和HPAI 两变量ADF 检验值比在10%显著性水平下的临界值都大，因此，不拒绝原假设，序列存在单位根，是非平稳的。但上述变量的一阶差分序列ΔLPAI 和ΔHPAI 均已平稳，可见上述变量均为一阶单整，即均为I(1)变量。

3.2 LPAI 和HPAI 两变量协整检验

有些时间序列数据虽然自身非平稳，但其某种线性组合却平稳，如果存在协整关系，这个线性组合就反映了变量之间有长期稳定的比例关系。

由于仅涉及LPAI 和HPAI 两个变量时间序列协整检验，可以采用EG 检验法，但EG 检验法的前提条件是LPAI 和HPAI 两个变量必须为同阶单整变量，从表1 可知，LPAI 和HPAI 两个变量是一阶单整变量，完全满足协整检验前提条件。EG 检验法分两步进行:

(1)选择因变量对自变量进行普通最小二乘法回归，得出最佳回归估计模型和估计残差序列项。

(2)对估计残差序列项进行单位根检验，如果残差序列项为平稳序列，则表明LPAI 和HPAI具有协整关系。

3.2.1 以HPAI 为因变量的协整检验

选择HPAI 为因变量，LPAI 为自变量，采用EViews5.0 进行回归模型的拟合，经过反复比较和剔除，并引入滞后项和自回归项，以得到最大回归解释能力的模型并通过相关检验。其回归模型结果如表2 所示。

表2 以HPAI 为因变量的回归模型结果

由表2 得到的回归模型为:

HPAIt= 13.321 52 + 0.462 496LPAIt－0.197 822LPAI(t－1)+0.613 854HPAI(t－1)+et

该回归模型的可决系数在99%以上，在5%显著性水平下通过了各项检验，拟合效果较好。相应残差序列e 的单位根检验如表3 所示。

表3 以HPAI 为因变量的回归模型残差序列e 的单位根检验

由表3 可知，残差序列项ADF 检验值比在1%显著性水平下的临界值还小，因此，拒绝原假设，回归残差序列不存在单位根，是一个平稳的时间序列。由此可以判断，LPAI 和HPAI 两者具有协整关系，即具有长期稳定的均衡关系。

综合表2 和表3，可以得到如下的结论:①房价对地价的弹性系数为0.462 496，即地价每增加1 个单位，房价将增加0.462 496 个单位;②在短期内，当期地价的上涨会引起当期房价的上涨，两者具有明显的同步效应，但当期地价对下一期房价的影响并不显著;③在短期内，当期房价的上涨会引起下一期房价的上涨，即存在房屋需求消费的棘轮效应。

3.2.2 以LPAI 为因变量的协整检验

选择LPAI 为因变量，HPAI 为自变量，采用EViews5.0 进行回归模型的拟合，经过反复比较和剔除，并引入自回归滞后项，以得到最大回归解释能力的模型并通过相关检验。具体回归模型结果如表4 所示。

表4 以LPAI 为因变量的回归模型结果

由表4 得到的回归模型为:

LPAIt=－34.066 030 + 1.009 275HPAIt+0.317 441LPAI(t－1)+ft

该回归模型的可决系数为98.9%，在1%的显著性水平下通过了各项检验，拟合效果较好。相应残差序列f 的单位根检验如表5 所示。

由表5 结论可知，残差序列项ADF 检验值比在1%显著性水平下的临界值还小，因此，拒绝原假设，回归残差序列不存在单位根，是一个平稳的时间序列。由此可以判断，LPAI 和HPAI 两者具有协整关系，即具有长期稳定的均衡关系。

综合表4 和表5，可以得到如下的结论:①地价对房价的弹性系数为1.009 275，即房价每增加1 个单位，地价将增加1.009 275 个单位。②在短期内，当期房价的上涨会引起当期地价的上涨，两者具有明显的同步效应。③在短期内，当期地价的上涨会引起下一期地价的上涨，即存在土地需求消费的棘轮效应。

表5 以LPAI 为因变量的回归模型残差序列f 的单位根检验

3.3 LPAI 和HPAI 两变量Granger 因果关系检验

上述协整检验结果证明了房价与地价之间存在长期的均衡关系，但是这种关系是否构成因果关系还需要进一步验证。因此，笔者采用Granger因果关系检验法作因果关系检验。

采用Eviews5.0，滞后期取值从1 ～14，房价与地价之间的Granger 因果关系检验结果如表6 所示。

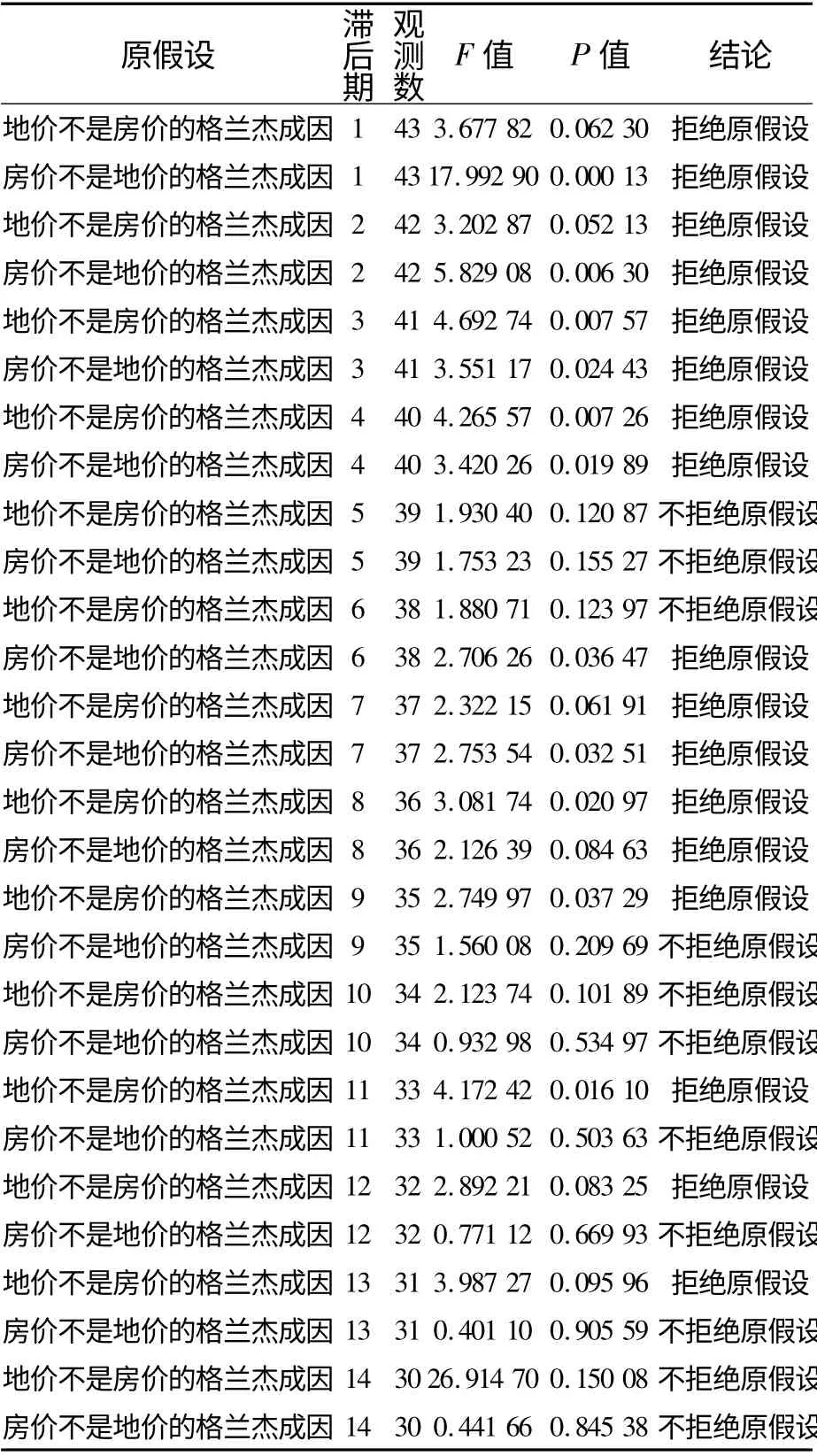
表6 房价与地价之间的Granger 因果关系检验结果

由表6 可知，在10%的显著性水平下，从短期看(1 年以内)，房价与地价互为因果关系，对应滞后期有1 ～4 个季度;从长期看，房价是地价的格兰杰成因，对应滞后期有6 个季度、7 个季度和8 个季度;同时，地价也是房价的格兰杰成因，对应滞后期有7 个季度、8 个季度、9 个季度、11 个季度、12 个季度和13 个季度。

4 结论及建议

通过上述分析，可以得出如下结论:

(1)房价和地价之间具有协整关系，两者之间存在长期稳定的均衡关系。其中，房价对地价的弹性系数为0.462 496，地价对房价的弹性系数为1.009 275。

(2)在短期内，当期房价(地价)的上涨会引起下一期房价(地价)的上涨，即存在房屋(土地)需求消费的棘轮效应。这种现象可能是受微观经济主体“买涨不买跌”的消费心理、优质房源的推出方式及土地资源的稀缺性三者的共同影响。

(3)房价和地价在即期内相互影响，两者具有明显的同步效应，其中，地价对房价的即期影响表现为地价是房价的成本因素，而房价对地价的即期影响表现为房价上涨预期下的土地“价高者得”供应模式。

(4)在短期内，房价与地价互为因果关系，对应作用时间在12 个月以内。从长期来看，房价与地价也互为因果关系，其中，房价对地价的平均作用时间约为24 个月，而地价对房价的平均作用时间约为30个月，显然，地价对房价的影响更为长远。

根据上述结论，提出如下建议:

(1)完善房地产信息发布制度，关注舆论，把握和引导市场预期，防止房价和地价信号被社会误读。

(2)坚持做好房地产市场监测监管，坚决打击房地产开发商“捂盘”和“囤地”行为，加大对开发商闲置土地行为的处罚力度。

(3)完善土地交易方式，合理安排供地节奏、数量和批次，形成均衡协调的供地结构;对于溢价率过高的用地，要及时调整出让方案，坚决放弃“价高者得”的用地供应模式;应尽量保证保障性安居工程用地，进一步加大普通商品住房用地的供应力度。

［1］ DICKS M J.A simple model of the housing market［R］.London:Bank of England，1990.

［2］ ALYOUSHA A，RICARDIAN C T.Causal ordering and relation between house and land prices:evidence from England［J］. Applied Economics Letters，1998(5):325－329.

［3］ CHEN M C，PATEL K. House price dynamics and granger causality:an analysis of Taipei new dwelling market［J］.Journal of Asian Real Estate Society，1998，1(1):101－106.

［4］ 高波，毛丰付.房价与地价关系的实证检验:1999—2002［J］.产业经济研究，2003(3):19－24.

［5］ 况伟大.房价与地价关系研究:模型及中国数据检验［J］.财贸经济，2005(11):56－63.

［6］ 宋勃，高波. 房价与地价关系的因果检验:1998—2006［J］.当代经济科学，2007，29(1):72－77.

［7］ 王岳龙，张瑜. 基于中国省级面板数据的房价与地价关系研究［J］. 山西财经大学学报，2010，32(1):50－57.

［8］ 陈会广，刘忠原.普通住宅房价与地价因果关系的检验及其政策含义［J］.产经评论，2011(1):57－64.

［9］ 刘闯，俞秋婷，高琴琴.基于联立方程模型的我国房价影响因素研究［J］.武汉理工大学学报:信息与管理工程版，2012，34(1):123－126.