双变量度量理论及引力的量子化

邵 丹，邵 亮，谢 勇

（1.江汉大学 光电信息研究所，湖北 武汉 430056； 2.武汉科技大学 理学院，湖北 武汉 430081；3.江汉大学 研究生院，湖北 武汉 430056）

0 引言

圈量子引力（LQG）出现之前，引力量子化大体有两种途径。一种是利用引入其他场、延展体、超对称等方法，企图使引力量子化。这些方法中除超弦M－理论外，其余皆因解决可重整性问题无望而无法发展。而M－理论中，关于引力相互作用的核心问题，目前也欠全面和具体的阐明，完成引力的最终量子化，还需长期的过程。另一种是在引力体制内进行引力的量子化。这种方法历史上提出的具体模式很多，其中最被推崇的是4－导数引力。这种理论是把General Relativity（GR）中的微分同胚变换当作规范变换［1］，将模式中的引力场用Faddeev 规范场量子化的方式量子化。其优点是可以用（引力）曲率平方项的引入消去引力的发散，理论在表现上具有可重整性。它需要解决的问题是，理论中存在负能量的粒子；若解决负能量问题，可能破坏S 矩阵的么正性。尽管如此，这一理论仍是协变方法实现引力量子化进行得最为彻底的一种理论。这一方法在引力量子化历史上曾引起不小的关注，如Rovelli 在文献［2］中回顾引力量子化简史时，曾例举过对Stelle［3］提出的4－导数引力量子化的评述。他指出，尽管4－导数引力存在需要进一步解决的问题，它仍被认为是解决量子引力问题的一种可行选择。Gambini 和Pullin 在文献［4］中谈到引力量子化的可重整性时，也指出了4－导数引力在作用量中引入高次项的方法可以用于治疗引力发散，不过应当去掉它为理论带来的非物理性质。同时，在论述空时性质时还指出，空时几何应具有非交换性质，这种性质与微观不确定性原理应相容。

利用量子化空时与引力的关系探讨引力的量子化，是LQG 发展出的一种新方法。这方面的一个例子就是Rovelli 的用空时4 单形剖分方法所做的引力子散射理论［5－6］。该理论把Regge 计算和量子场论中的连续场的量子化方法，利用空时的微观离散性质和四面体的量子特性，做了明确的推广。这开启了用量子化的空时研究引力量子化的先例。不过，理论中仍然存在自旋网顶角结网算子以及低能极限等的不确定性，需要进一步研究，目前还远非是理论上无需质疑的结果。

笔者认为，引力量子化与空时量子化及其微观性质有关。把空时量子化后的信息引入到引力量子化中来，可去掉或改善引力量子化遇到的困难，甚至如上困难。Rovelli 的上述工作，就是借用空时的量子剖分特性表述的一种引力的量子化。

针对如上现实，本文仍用作用量中的曲率平方项来抵消引力发散，不过曲率平方项并不取决于引力扰动，而是由量子化后空时的度量决定。从而理论中将不出现负能粒子，也不存在为了消去负能粒子而可能破坏么正性的问题。而且与其他高导数理论不同，它的引力部分保持与GR 相同，量子化后也不存在其他非物理结果。

1 空时与引力的双变量度量统一理论

1.1 双变量度量

本文中的空时与引力是在LQG 中发展出的两个完全不同的概念，空时并不指引力，引力也不指空时。Minkowski 空时M′ 是本文空时的平坦极限，一般空时可以弯曲，记以M 。 M 的弯曲是自身独立的弯曲，与其中引力的存在与否无关。GR 是把平坦Minkowski 空时M′ 的度规ημν和引力扰动hμν(x)结合在一起的空时与引力的统一理论。LQG 对空时量子化的研究表明，量子化空时M 自身的度量将允许有量子起伏，这里记为ημν(x)，从而M 可具有与引力存在与否无关的弯曲，即空时弯曲。 M 中有引力扰动hμν(x)存在时，得到的流形记为M，即M 是空时与引力的二元世界。熟知，M′是M 的抽象平坦特例，M′中存在引力扰动hμν(x)时，得到的流形则记为M′。M′在本文中是空时M′与引力混成的4 维流形，而在GR 中被称为“弯曲时空”。

由于空时和引力都可使流形M 弯曲，据文献［7］，M 的度量将由如下双变量度量构成：

式中重复相乘指标不求和，ημν(x)=εμν(x)ημν，εμν(x)为空时度量演变参量。当εμν(x)≡1 时，（1）式为GR 中的度规表达式。（1）式中的εμν(x)与hμν(x)分别是空时度量扰动与引力扰动，二者是独立的，都对组合度量ℊμν(x)有贡献。

1.2 双变量度量空时与引力统一理论的作用量与场方程

该理论研究的对象为空时与其中的引力，二者形成的二元世界M 的本体是空时M ，M 上的织绣是引力扰动hμν(x)。流形M 的度量为合成度量ℊμν(x)，它的作用量为

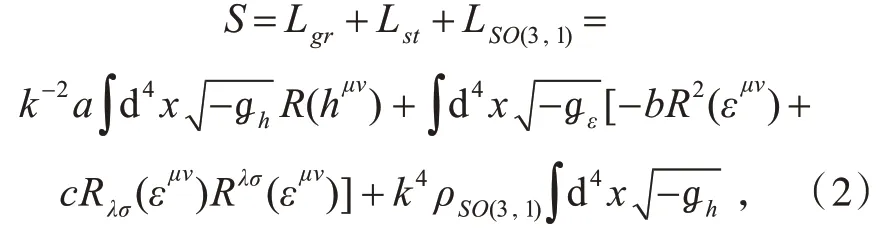
将二元世界的作用量（2）式分别对引力扰动hμν(x)和空时度量扰动ημν(x)求变分，可得该统一理论的两组场方程。

将作用量（2）式利用通常变分原理

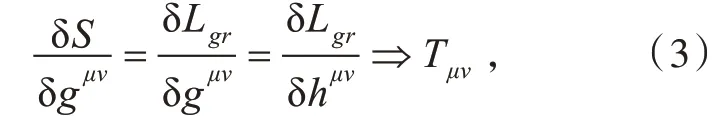
式中ℊμν为时空度规，Tμν为GR 的质量张量，将得到该统一理论的引力场方程

式中Gμν(hλσ)为统一理论的引力爱因斯坦张量，其表达式为

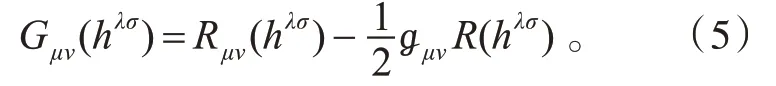
把作用量（2）式对空时度量扰动ημν(x) 变分，即

该统一理论的空时度量方程如下：

式中不同形式的曲率以及统一理论的空时爱因斯坦张量Gμν(ελσ)，皆由组合度量（1）式中的ημν(x)规定，且皆作为基本变量εμν(x)的泛函。对于统一理论的空时爱因斯坦张量，它的表达式如下：

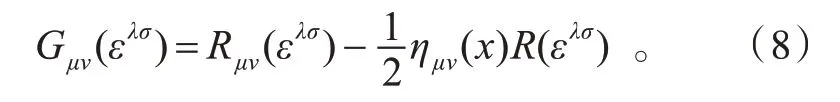
（7）式的意义在于，在该模式中，空时与引力虽然可以进行统一描述，但空时自身具有独立的演化机制，它是空时理论中的一组新方程。对空时M 这种演化机制的刻划，是该双变量理论的重要结果，也是它与GR 的重要区别。作为特例易知，Minkowski 空时M′ 是（7）式的一个特解；另外，Rμν=0 的空时也是（7）式的特解，而后者是可以弯曲的。

2 双变量度量空时与引力统一理论的引力量子化

根据作用量（2）式，利用通常的规范场协变量子化方法，可把该统一理论中的引力进行量子化。为此，选量子化Green 函数生成泛函Z 的规范固定项

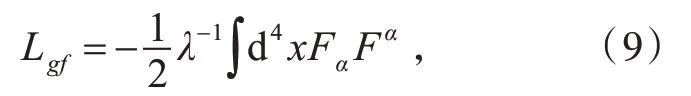
式中λ 为规范固定参数，

鬼项与外场项分别为

式中ξ 为空时任意无穷小矢量。

利用（2）、（9）、（10）和（11）各式定义的拉氏量Lgr、Lst、Lgf、Lgh和Lef，可得到用于引力量子化的约简有效作用量为

式中Leff为该理论引力量子化的有效作用量，且有

求出该理论引力子自由传播子和各种散射传播子。这里把引力自由传播子和引力相互作用3 顶角给出于后。

对于引力子自由传播子，可将（2）式中的Lgr对hμν(x)完（引力扰动）展开，展开式中h2项将贡献这一传播子，同时规范固定项Lgf也将贡献这种传播子。现将结果直接给出如下：

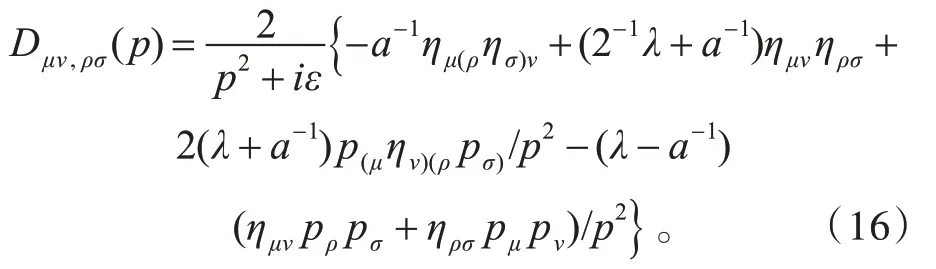
类似地，将Lgr的展式中的h3项收集齐全，通过下式

可得该双变量统一理论中的引力子3 顶角，现将如此得到的一结果列出如下：

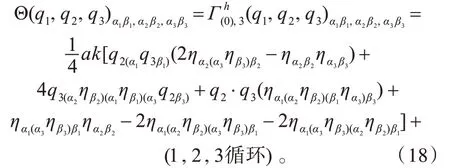
该理论中鬼与反鬼粒子的引入，是为了使理论具有最大完备性（对称性），这种粒子将参与相互作用描述，但并无观测效应，对其要求是保证理论自恰。

3 重整化

3.1 发散分析

该理论存在的引力自身的传播子，有2 点、3点、4 点、……散射传播子，由这些传播子按Feynman 规则编织出的相互作用图，将不可避免地出现由粒子动量标定的圈图，这些圈图在积分中的无穷大贡献必须用正规化和重整化手续消去。文献［3］已经用协变手段为4－导数引力的量子化得到了正规化结果，现直接给出如下：

式中Pμν为引力子的反对易外场。在LQG 体制下，解（20）和（21）这两组方程，将有［3］

式中Sμν和Tτσ是引力场hμν的任意Lorentz 协变函数。这里需要指出的是，该理论中虽然存在两个独立变量，但二者构成的仍是一个统一的度量。同时，由于Gauss－Bonnet（G－B）定理的存在，将使得（22）式中的泛函I(hμν)是hμν以及它的0、2、4 导数的任意规范不变的定域泛函。

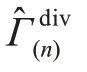
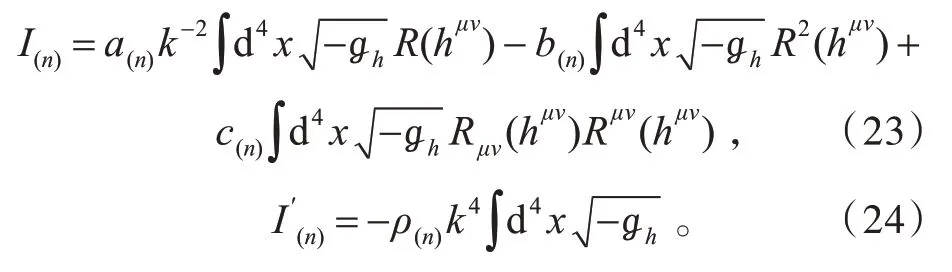
3.2 发散消除

3.2.1 双变量度量理论的引力重整化Ⅰ——曲率0、1 次方型发散的消除 从发散表达式（23）和（24）可知，这一理论有关引力的发散共有4 种。我们先给出（23）式右侧第一项

对于I(n)中的第二项和第三项

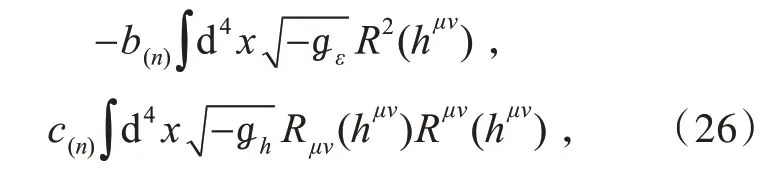
与文献［3］不同，由于（2）式中的曲率平方项不是引力扰动hμν的泛函，而是εμνημν的泛函，利用εμνημν作为函数变量，并采取如上直接构成符号相反结构相同的抵消项来抵消（26）式中的曲率平方型发散，并不能保障数量上真正抵消。这是因为，与4－导数引力不同，这里的hμν和εμν是两个相互间独立的变量，而4－导数理论只具有hμν作为变量。从而，需要进一步使用不同的重整化技术。

3.2.2 双变量度量理论的引力重整化Ⅱ——曲率2 次方型发散的消除

1）组合度量的重整

首先从如下形式的组合度量

开始讨论。前面曾指出，组合度量（27）式是在微观Planck 尺度用等价类手段得到的结果。GR 是在宏观利用Riemann 几何，并通过等效原理，使这一组合度量中的引力扰动hμν(x)，写在了平坦Minkowski 空时背景之上，从而有了GR 中的组合度规表式

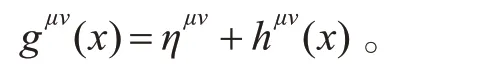
这样一来，在GR 中便引入了平直度规ημν。同时，也把狭义相对论作为了它的极限(hμν→0)理论。我们认为，空时作为质地，它的度量εμν(x)ημν具有抵消引力扰动产生发散的作用。为此，它将有与hμν(x)等量的一部分度量被“消耗”。将这一部分记为(εμν(x)ημν)E，则数值上将有等式

这里称(εμν(x)ημν)E为空时重整化折合度量。这里需要指出的是，(εμν(x)ημν)E为εμν(x)ημν中折合出来的一部分，它在数值上与hμν(x)相当，但其本身并非是引力扰动，故而，不贡献引力子。这一性质十分重要，它可用于消除引力相互作用中出现的发散，且不出现负能粒子。另一方面，

中，因用于重整化而剩下的部分

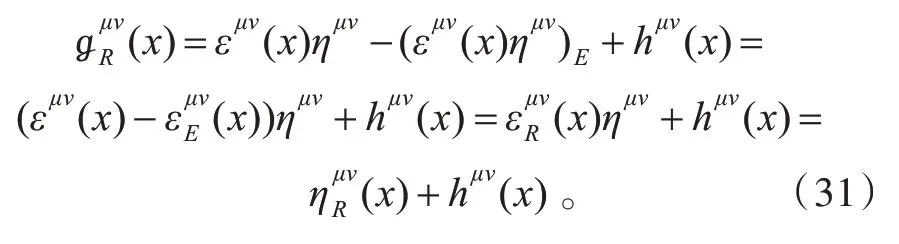
2）作用量的重整

现在考虑作用量。在如上双变量组合度量的重整化方程式下，也将导致作用量（2）式发生改变。（2）式给出的经典作用量S 包括三部分贡献。其中LSO(3，1)在重整化过程中并不发生改变。重整化后的Lgr表达式未改变，不过其中的组合度量ℊμν(x) 需用重整化后的组合度量ℊμν，R(x) 代替。另一发生改变的是空时作用量Lst，现在给出Lst在这一重整化过程中的改变。它的表达式为

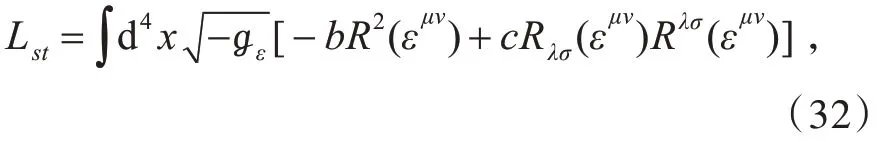
式中中间变量 εμν(x) 表征的是空时度量εμν(x)ημν。在考虑了如上组合度量重整化

后，由于组合度量ℊμν(x) 中的空时度量εμν(x)ημν被分解成两部分：

这将导致作用量Lst将分别由如下两个作用量代替：

式中

利用（35）式，把（36）和（37）式代入（2）式，将有考虑了如上重整化前、后的作用量改变

之后的双变量理论的作用量。把得到的这一作用量记为SR，则有

3）引力发散的最终消除

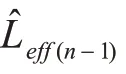
如上用逐阶抵消的方法，消除了（23）和（24）式给出的n 圈阶出现的全部发散。

4 结论

该双变量理论中，认为空时与引力是完全不同的两种概念，它们具有严格区别外，也存在联系［7］。GR 由于自身的体制不能把引力与空时彻底剥离，它的量子化无法找到适当方法得以有效地进行。本文在分别把它们用变量εμν和hμν做彻底的分离表述后，将量子化的空时质地M 提供的信息输入到引力的量子化方程式之中，自恰地克服了以往遇到的困难，完成了一种引力的量子化与重整化的最终研究。

该双变量理论中空时M 的几何以及描述引力激发与跃迁的几何均是LQG 中的非交换几何［9］，从而为引力量子化的研究重新打下了合理的基础。

由于空时M 按G－B 定理提供的拉氏量Lst，与4－导数引力不同，是定义为空时变量εμν的泛函，从而重整化后，它一部分（即Lst，E）将用于抵消引力发散，而另一部分（即Lst，R）将支配空时M 本身的度量演化。这一方面使理论中的引力部分与GR 相同，不出现负能粒子；另一方面，也不再出现与现实物理不相容的多余结果。从而对传统高导数理论引力量子化遇到的问题进行了技术上的解除。解除的关键是把LQG 中空时量子化的信息引入到了引力量子化中来。这说明，引力并不像传递其他相互作用力的粒子那样，只把空时作为背景，即可实现自身的存在与量子化；而是告诉我们，引力与空时既有严格区别，又有相互间的深刻联系。这种区别与联系未阐明之前，引力的量子化不会得到成功。物理学告诉我们，引力场必须与描述空时的度规进行合成，才能得以彻底描述。这是引力的特征，不仅在宏观如此，在微观量子化水平更是如此。这也注定了引力量子化并不排除沿用通常场的量子化方法，但也必须考虑它的特殊之处，最主要的是考虑空时量子化与引力量子化间的关系。否则，按LQG，引力的量子化无法独立地获得与量子化空时自恰的结果。也就是说，要在空时与引力二者量子化的共同研究中，实现引力的量子化。

［1］ Capper D M，Ramón Medrano M. Gravitational Slavnov－Ward identities［J］. Phys Rev D，1974，9（6）：1641－1647.

［2］ Rovelli C. Quantum gravity［M］. New York：Cambridge University Press，2004.

［3］ Stelle K S. Renormalization of higher－derivative quantum gravity［J］.Phys Rev D，1977，16（4）：953－969.

［4］ Cambini R，Pullin J. Loop quantum gravity［M］. New York：Oxford University Press，2011.

［5］ Rovelli C. Gravition propagator from background－independent quantum gravity［J］. Phys Rev Lett，2006，97（15）：151301－151304.

［6］ Modesto L，Rovelli C. Particle scattering in loop quantum gravity［J］. Phys Rev Lett，2005，95（19）：191301－191304.

［7］ 邵丹，邵亮，邵常贵. 一种空时体积与引力的激发和跃迁生成模式［J］. 物理学报，2011，60（12）：120401－120404.

［8］ Peskin M E，Schroeder D V，Martinec E. An introduction to quantum field theory［J］. Phys Today，1996，49（8）：69.

［9］ Shao D，Shao L，Shao C G，et al. Black hole entropy and area quantum entanglement originated from spin networks［J］. International Journal of Modern Physics A，2010，25（7）：1339－1347.