非线性动力学方法在声带息肉和囊肿患者嗓音信号分析中的应用△

余明强 徐新林，2 张赛 张宇 郭永清，2 林生智，2 庄佩耘 蒋家琪

嗓音声学分析是运用电子声学的方法对嗓音的物理特性进行客观分析，为无创性的辅助诊断方法，其方法主要有传统的扰动方法和非线性动力学方法。扰动方法是基于提取基频的经典傅里叶变换方法，由此发展起来的基频（F0）、频率微扰（jitter）和振幅微扰（shimmer）等已成为嗓音声学评估的重要指标，在临床和科研中应用广泛。傅里叶变换用于分析不规则信号时会发生与原信号的声学特性不相关，仅适用于规则的或次规则的嗓音信号，当用其分析复杂的不规则嗓音信号时可能会出现较大的偏差［1，2］。非线性动力学方法对状态扰动具有高度的敏感性，状态的极小扰动将导致状态差被迅速放大，最终可产生完全不同的输出，适用于简单的周期运动及复杂的混沌信号，主要反映信号的不规则的物理特性，目前，该方法在嗓音医学中主要应用于实验研究阶段和发音机制的研究。

实验证实声带的振动和嗓音信号具有非线性特性［3～8］，Baken［7］应用分形维定量测量正常声带振动周期，发现了声带振动的不规则性。Titze［8］从非线性动力学的角度，把嗓音信号定性地分成三类：第1类信号是周期或者似周期信号，含有强烈的基本频率；第2类信号含有强烈的周期调制或次谐波；第3类信号是非周期的混沌信号和噪声。扰动方法（jitter、shimmer）只适用于第1 类信号，不适用于第3类信号，而非线性动力学方法适用于分析这三类信号。嗓音客观声学评估在临床上具有重要的参考价值，本研究应用扰动方法和非线性动力学方法分析正常人、声带息肉和声带囊肿患者的嗓音信号，探讨其在嗓音声学评估中的应用价值。

1 资料与方法

1.1 临床资料 20 例正常受试者来自厦门自愿者，男8例，女12例，年龄18～50岁，平均25±5.2岁，无声嘶、咽喉部疼痛等嗓音疾病症状，职业用嗓者或受过嗓音训练者除外，既往无嗓音疾病或外伤，无吸烟、呼吸道疾病病史。嗓音疾病患者55例，年龄18～50岁，病程在2月～2年，其中声带息肉患者29例，男14例，女15例，年龄32±11.08岁，病程4.34±2.04月；声带囊肿患者26例，男11例，女15例，年龄34.8±10.02岁，病程6.75±6.43月，测试时均无上呼吸道疾病，术后均经病理确诊。

1.2 嗓音信号收集 受试者于声音屏蔽室内，站位，麦克风与水平线成15°角，口距话筒15cm 左右，平稳发元音／a／3次，每次持续5～10秒，从声样中提取平稳段（3.0秒），采样频率44.1kHz，运用Kay PENTAX－Multi－Speech 软件中的Multi Dimensional Voice Program（MDVP）Model5105 系统收集嗓音信号。

1.2.1 传统扰动分析方法 收集受试者嗓音信号后，由MDVP 软件获得jitter和shimmer值，取3次数据的平均值，根据jitter值和shimmer值的参考范围，jitter值大于5和／或shimmer值大于20的数据视为不可靠，除去该项数据和该受试者的嗓音信号［1］。

1.2.2 非线性动力学方法 取3次信号中较为平稳的一段信号进行相空间重构和计算关联维。基于Parkard等［9］提出的时间延长技术方法形成重构相空间，对于任何维数的动力系统，都可以表示：

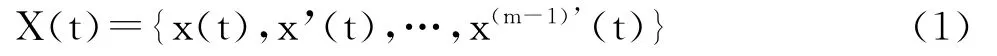
用时滞变量和它的延迟时间τ变量x（t＋τ）代替x’（t），得到延迟坐标矢量：

τ是延迟时间，根据交互信息方法选择最优延迟时间即交互信息量第一次降到最低并开始上升时的延迟时间（图1），m 是嵌入维数。时间延迟向量决定了相空间重构的图形，相空间重构的点均选择10 000点，如图2。Takens等［10］从数学上证明了在m＞2D＋1（D 为系统的维数）时，即对于D2，当m＞5时重构相空间与原始相空间是等同的。根据Fraser［11］提出的交互信息程序评估最优延迟时间τ（图1）。由于关联维D2比较简单，且在大量数字中的快收敛率和描述不规则行为的有效性，已被广泛应用［12］。噪声的关联维D2 随着嵌入维数m 的增加不会出现收敛，而混沌系统的关联维D2 会达到限值。关联维D2的计算如下（Pawelzik and Schuster，1987）：

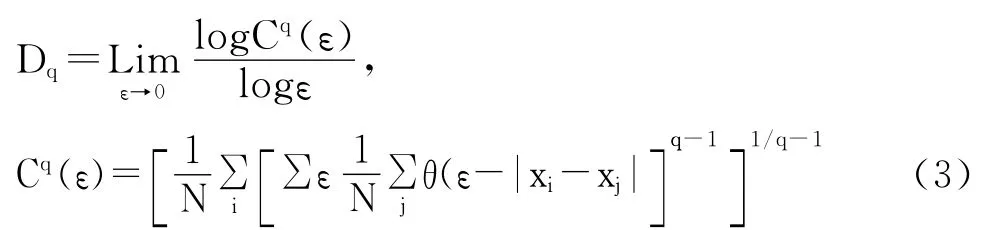
当q=2时，Dq将减少成为D2。∮（x）满足：如果x＞0，∮（x）=1；如果x≤0，∮（x）=0。当m 非常大时，Dq将在缩放处出现收敛。噪声不会出现收敛，关联维D2出现收敛，收敛处即为D2值的大小，如图3。

1.3 统计学方法 采用SPSS17.0软件，计算受试者jitter、shimmer和关联维D2值的均数和标准差，采用Mann－Whitney U 非参数检验。将声带息肉、声带囊肿患者作为异常嗓音组与正常受试者的jitter、shimmer和D2 值作ROC 曲线（受试者工作特征曲线：反映敏感性和特异性变量的综合指标，是用构图法揭示敏感性和特异性的关系，以敏感性为纵坐标、1－特异性为横坐标绘制成的曲线，曲线下面积越大，表示诊断准确性越高）分析。

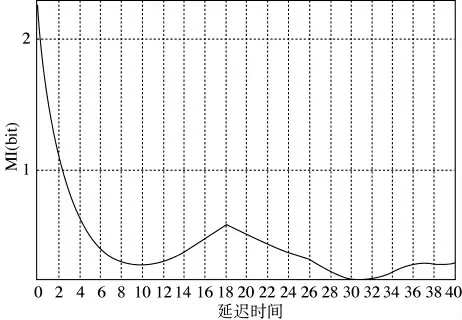
图1 交互信息与延迟时间图 根据交互信息方法选择最优延迟时间，交互信息量第一次降到最低并开始上升时的延迟时间为最优延迟时间

2 结果

2.1 实验结果 75例受试者中有3例患者的jitter值大于5、shimmer值大于20以及2例shimmer值大于20，除去这5例患者的数据。图2为声带囊肿患者（图2a）和正常受试者的重构相空间（图2b），可见，声带囊肿患者相空间重构图中点的轨迹更加凌乱，较正常受试者没规则。图3 为关联维D2 收敛图形，正常受试者关联维D2（图3a）较声带息肉患者关联维D2（图3b）更低值处收敛。图4为正常人及声带息肉患者嗓音信号的波形和功率谱，可见，声带息肉患者的嗓音声学信号的波形和功率谱（a和b）较正常受试者的波形和功率谱（c和d）没有规则。

图2 声带囊肿患者（a）和正常受试者（b）重构相空间

图3 正常受试者（a）和声带息肉患者（b）的嗓音声学信号的关联维D2在收敛处的图形 嗓音关联维D2随嵌入维数增加出现收敛，噪声不会出现收敛

图4 声带息肉患者（a、b）和正常受试者（c、d）声学信号的波形和功率谱

2.2 统计学分析结果 声带息肉和声带囊肿患者的jitter、shimmer和D2值的均数均高于正常人，差异有统计学意义（P＜0.05）；两种嗓音疾病患者之间，jitter、shimmer和D2值差异均无统计学意义（P＞0.05）（表1）。ROC 曲线显示jitter、shimmer和D2值在ROC曲线下的面积分别为0.957±0.022、0.951±0.026和0.862±0.047，与0.5相比，差异均有统计学意义（P＜0.001）（图5）。

表1 70例受试者声学信号分析结果（±s）

表1 70例受试者声学信号分析结果（±s）

组别性别例数（例）jitter（%）shimmer（%）D2正常男8 0.34±0.07 2.01±0.85 1.56±0.16女12 0.50±0.28 2.27±0.94 1.26±0.18总20 0.42±0.24 2.14±0.89 1.41±0.21声带息肉男13 2.78±1.34 8.94±3.62 2.88±1.47女13 2.58±1.44 6.29±3.15 1.98±0.71总26 2.68±1.23 7.62±3.34 2.43±1.09声带囊肿男14 1.94±0.99 6.58±1.00 2.28±0.70女10 2.81±1.57 4.90±2.00 1.62±0.40总24 2.38±1.42 5.89±1.55 1.85±0.62

图5 声带息肉、囊肿患者与正常受试者的D2、jitter、shimmer值的ROC曲线

3 讨论

目前，对嗓音声学信号的分析主要包括传统的扰动方法、频谱分析和非线性动力学方法。扰动方法的计算方法依赖于周期的或近似周期嗓音声学信号而具有一定的应用限制［1］。当嗓音声学信号不规则时，难以提取稳定的基频，导致计算jitter 和shimmer值时出现较大误差［1］。本实验中即有5例患者的jitter值和／或shimmer值过大，频率和振幅的扰动大，提取的基频不稳定，不能应用扰动方法分析。频谱分析可以很好地观察嗓音声学信号有无异常，但不能为嗓音信号提供稳定的定量估计，由图1可见，嗓音疾病患者的嗓音信号波形及功率谱比正常受试者不规则，两者对应的频谱虽然可以看出差异，但很难用一个定量的指标反映其不规则的程度。非线性动力学分析方法在生物医学中已被广泛应用［13］，主要是对生物医学信号的几种非线性动力学参数的计算并比较分析，其中D2 参数适合于周期的和非周期的嗓音信号，D2的计算和分析已被多次成功应用于分析嗓音声学信号［14～16］。

非线性动力学方法能够分析辨别出正常和异常嗓音声学信号［6，16］，本研究结果显示，声带囊肿患者的相空间重构图中点的轨迹更加凌乱，较正常受试者无规则；正常受试者关联维D2 较声带息肉患者在更低值处收敛，两种嗓音疾病的D2 值均大于正常者，说明非线性动力学方法能分辨出正常和异常嗓音信号。ROC曲线分析显示D2值与0.5相比有显著性差异（P＜0.001），但与Jiang等［5］研究中声带小结与声带息肉两种嗓音疾病之间的D2值有明显差异的结果不同，本研究中声带息肉和声带囊肿患者两种嗓音疾病之间的嗓音声学信号D2值差异无统计学意义（表1），两种嗓音疾病患者用扰动方法分析得出的jitter和shimmer之间差异也无统计学意义，说明非线性动力学方法和扰动方法均不能鉴别出这两种嗓音疾病的嗓音声学信号，可能是因为这两种声带病变对声门周期的扰动有相似的影响。Chai等［17］研究发现男性吸烟者嗓音声学信号的D2值比正常人更高，在评估病态嗓音方面比扰动方法有更好的敏感性。而从文中ROC 曲线分析结果来看，D2 值曲线下的面积稍低于jitter 和shimmer值，表明对于较规则的嗓音声学信号，扰动方法分析的结果具有更好的特异度，更适合用扰动方法来分析。

从表1中可以看出正常男女D2值均大于1，表明正常嗓音声学信号也不是绝对周期性的，正常和异常患者的嗓音信号的关联维值D2均小于4，表明正常人、声带息肉和声带囊肿患者嗓音信号均具有低维的特征，与Zhang等［18］研究的单侧声带息肉有限元模型模拟的声带振动动力学结果相似。Berry等［19］研究离体狗喉发声信号时认为声带发声条件的任何变化均会导致每次声门周期发生轻微的变化，在经历多次声门周期的迭代之后，总体的声带振动是不稳定的和不规则的，产生的嗓音信号也是不规则的。文中两种嗓音疾病患者嗓音信号的D2值大于正常受试者嗓音信号，表明两种嗓音疾病患者的嗓音信号比正常受试者更不规则、更复杂。

虽然扰动方法中jitter、shimmer值的计算依赖于提取稳定的声信号，使其临床应用受到一定的限制，但其描述的是嗓音声学信号的周期和振幅的差异变化，由此产生的包括频率、声强、噪声谱和共振峰等20几个指标，描述了声学信号不同方面的物理特性，其临床价值是非线性动力学方法不能取代的。声带振动受声带的位置、形状、质量、张力、弹力及粘滞性等多因素影响，因此病变声带的振动不可能只按照某一因素的变化产生线性的变化，而是受多因素的变化而产生非线性现象，非线性动力学方法计算的维、熵、李亚普诺夫指数等指标主要描述的是信号的不规则和复杂程度，适用于分析更加复杂的嗓音信号，且符合病变声带振动产生异常嗓音信号的病理生理过程。D2描述的是嗓音信号的几何特性，从总的方面评估嗓音信号之间的差异。本研究显示，可用非线性动力学方法分析扰动方法分析出现较大误差的5例患者的嗓音声学信号，表明非线性动力学方法在嗓音医学临床上具有更广的适用性和更好的实用性，可作为扰动方法的重要补充。

与扰动方法强调线性、规则和频率的概念不同，非线性动力学方法强调了异常嗓音信号的非线性、不规则性和复杂性，分析规则向不规则的转化，带有明显的间断性，参量的微小变化导致运动形式大的变化，导致行为的不规则。但非线性动力学方法并不能代替现有的扰动分析方法，而是为异常嗓音信号分析提供一种新的方法和更多的信息，从而更全面地分析嗓音声学信号。

1 Titze IR，Liang H.Comparison of F0extraction method for highprecision voice perturbation measurements［J］.J Speech Hear Res，1993，36：1 120.

2 Yu P，Garrel R，Nicollas R，et al.Objective voice analysis in dysphonic patients：new data including nonlinear measurements［J］.Folia Phoniatr Logop，2007，59：20.

3 Robb MP.Bifurcations and chaos in the cries of full－term and preterm infants［J］.Folia Phoniatr Logop，2003，55：233.

4 Zhang Y，Jiang JJ，Biazzo L，et al.Perturbation and nonlinear with unilateral laryngeal paralysis［J］.J Voice，2005，19：519.

5 Jiang JJ，Zhang Y，MacCallum J，et al.Objective acoustic analysis of pathological voices from patients with vocal nodules and polyps［J］.Folia Phoniatr Logop，2009，61：342.

6 Zhang Y，McGilligan C，Zhou L，et al.Nonlinear dynamic a－nalysis of voices before and after surgical excision of vocal polyps［J］.J Acoust Soc Am，2004，115：2 270.

7 Baken RJ.Irregularity of vocal period and amplitude：a first approach to the fractal analysis of voice［J］.Journal of Voice，1990，4：185.

8 Titze IR.Workshop on acoustic voice analysis：summary statement［J］.Denver，National Center for Voice and Speech，1995，1：36.

9 Packard NH，Crutchfield JP，Farmer JD，et al.Geometry from a time serise［J］.Phys Rev Lett，1980，45：712.

10 Takens F.Detecting strange attractors in turbulence［J］.Springer Lecture Notes Math，1981，898：336.

11 Fraser AM，Swinney HL.Independent coordinates for strange attractors from mutual information［J］.Physical Review A，1986，33：1 134.

12 Grassberger P，Procaccia J.Measuring the strangeness of strange sttractors［J］.Physica D：Nonlinear phenomena，1983，9：189.

13 Poon CS，Merrill CK.Decrease of cardiac chaos in congestive heart failure［J］.Nature，1997，389：492.

14 Hornero R，Alonso A，Jimeno N，et al.Nonlinear analysis of time series generated by schizophrenic patients［J］.IEEE Eng Med Biol Mag，1999，3：84.

15 Moon FC，Hilborn RC.Chaotic and fractal dynamics：an introduction for applied scientists and engineer［J］.American Journal of Physics，1993，61：670.

16 Jiang JJ，Zhang Y，Ford CN.Nonlinear dynamics of phonations in excised larynx experiments［J］.J Acoustic Soc Am，2003，114：2 198.

17 Chai LY，Alicia JS，Zhang Y et al.Perturbation and nonlinear dynamic analysis of adult male smokers［J］.J Voice，2011，25：342.

18 Zhang Y，Jiang JJ.Chaotic vibration behaviour of a vocalfold model with a unilateral polyp［J］.J Acoust Soc Am，2004，115：1 266.

19 Berry DA，Herzel H，Titze IR，et al.Bifurcations in excised larynx experiments［J］.J Voice，1996，10：129.