晶圆预对准系统误差仿真分析*

李学威，孙义田，何伟全，张 鹏，陈守良

(1.沈阳新松机器人自动化股份有限公司，沈阳 110168;2.东北大学 机械工程与自动化学院，沈阳110819)

0 引言

晶圆预对准是晶圆搬运以及整个IC 制造过程中的重要环节，晶圆的定位与识别都需要预对准机(Prealigner)的参与。晶圆预对准的目的是计算晶圆的偏心并找到其缺口(notch)，进而补偿其偏心并将缺口转到预设方向，为下一步的晶圆识别或处理做好准备。文章［1］～［6］对晶圆偏心及缺口的识别方法进行了理论计算和实验，验证了晶圆预对准方法的有效性，其不足之处在于，对晶圆预对准误差分析不能反映出包括转动中心偏置、晶圆初始放置状态等因素在内的其他误差的综合影响。

本文以新松机器人公司开发的预对准机(图1)为分析对象，建立了预对准机的数学模型，对包括CCD 的精度、转动中心偏置及晶圆初始放置状态等多种误差因素进行了仿真分析，得到了多种误差影响下的晶圆对准误差的变化规律，对预对准系统的改进提供了理论指导。

图1 预对准系统组成图

1 晶圆预对准原理及仿真模型的建立

参考图1，预对准机的工作原理是:首先将晶圆放置到三个顶针上，然后旋转吸盘将晶圆托起，再将晶圆旋转一周，由线阵CCD 传感器检测晶圆的边缘位置和缺口位置，并将位置数据传送至数据处理系统进行晶圆圆心的计算。装置将计算后的数据(偏心量)传送至晶圆传输机械手，机械手将晶圆抓起，调整晶圆圆心的绝对位置。随后晶圆再次被本装置托起并按计算数据旋转至一定角度，实现晶圆的对准。

晶圆的边缘主要由两部分组成，如图2 所示:圆周和缺口(notch)。其中缺口部分由两直线段N1N2、N3N4夹一圆弧段N2N3构成。其中N1、N2、N3、N4为缺口各部分的端点。根据SEMI 标准中给出的晶圆缺口尺寸，缺口的总跨度约为1.04°，深度约为1mm，其中相对平缓的圆弧段N2N3的跨度约为0.49°。

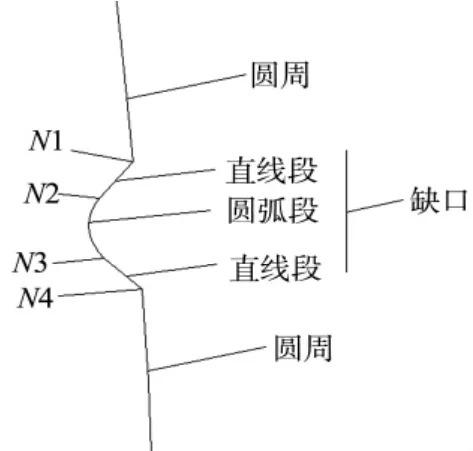
图2 晶圆边缘组成

如图3 所示，为预对准原理图，预对准机以吸盘吸附带动晶圆绕转动中心转动，并由设置在晶圆边缘附近的线阵CCD 传感器来采集晶圆边缘的信息，使晶圆转动一周，可获得转动过程中每一转角所对应的晶圆边缘与CCD 线阵所在直线交点P 的信息，即OP 的长度［1］。理论上，晶圆的转动中心应当处在CCD 线阵所在直线上，但实际上，由于制造及装配存在误差，晶圆实际的转动中心会相对理论转动中心产生一定的偏置，设O 为晶圆理论转动中心，O'为晶圆实际转动中心，OO'即为转动中心的偏置。

根据图3 所示的模型，以晶圆理论转动中心O为原点，并以通过O 点的CCD 线阵所在直线为X 轴建立坐标系XOY。设晶圆实际转动中心O'与理论转动中心O 的距离OO'为e，OO'相对X 轴的转角为a;晶圆圆心为C，晶圆偏心量O'C 长度为d，O'C 相对OO'的转角为t。晶圆缺口顶点与晶圆圆心C 所在直线连线相对O'C 转角为b。晶圆边缘与CCD 线阵所在直线交点为P。当晶圆转动时，随着t 的变化，OP长度也会随之变化。

设OP 长度为L，晶圆半径为R，则当晶圆圆周与CCD 线阵所在直线相交时，由图3 所示的几何关系可推导出L 与以上各参数之间的关系:

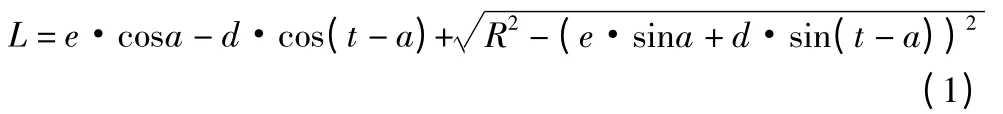
类似地，可得到晶圆缺口部分与CCD 线阵所在直线相交时的L 的方程。思路是，首先假设晶圆缺口部分各段端点与CCD 线阵所在直线相交，再根据几何关系反推出各自情况下的转角t(tc1、tc2、tc3、tc4)，然后建立分段函数求得各段交点，得到相应的缺口模型(本文未列出缺口模型的计算公式)。

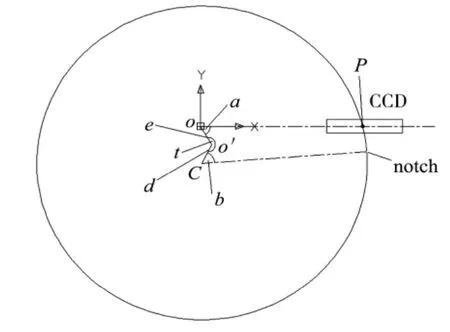
图3 预对准原理图

对模型进行仿真验证，取经验值:

对整个圆周按相同间隔的转角均匀的采集4800组数据，并对采集结果加入随机误差，取CCD 的精度为0.03mm，仿真结果如图4 所示，该结果与实际采集数据的变化趋势一致。

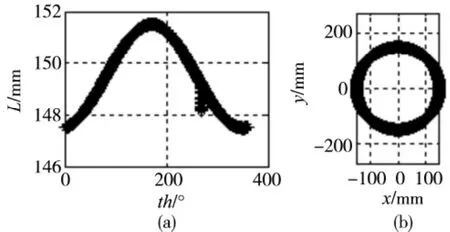
图4 晶圆边缘原始数据采集仿真

2 误差仿真分析

下面基于仿真模型，晶圆初始放置状态、晶圆转动中心偏置及CCD 精度等影响晶圆偏心及缺口识别精度的几个误差来源分别进行分析。

2.1 晶圆初始放置状态对识别误差的影响仿真

晶圆初始放置状态包括不同的晶圆偏心量和偏心角，分析两者的大小对识别误差的影响有利于识别算法的改进与整机性能的验证。

不考虑晶圆中心偏置(设e =0)，即假设晶圆实际转动中心O'与理论转动中心O 重合。设置CCD的精度为0.03mm，由节1 建立的模型仿真得到晶圆偏心量识别误差dd 及偏心角识别误差dth 与晶圆偏心量和偏心角大小的关系图(图5 和图6)。利用最小二乘圆拟合法得到晶圆在初始位置时的圆心坐标为［2-3，6］:(－1.2772，1.5395)，与理想情况相比存在误差，但误差不超过0.01mm，是可以接受的。而把拟合得到的圆心坐标表示成极坐标的形式为(2.0003，129.6785)，即晶圆偏心量为2.0003mm，偏心角为129.6785°。偏心量的识别误差较小，几乎可以忽略不计，但偏心角的识别误差却较大，达到了0.3215°。

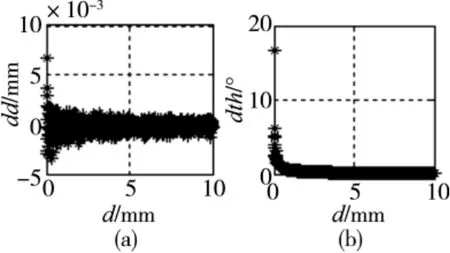
图5 晶圆初始状态对偏心识别误差影响

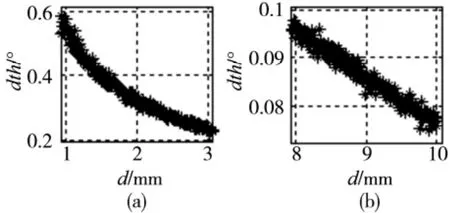
图6 晶圆初始状态对偏心角的识别误差影响

2.2 转动中心偏置对识别误差的影响仿真

这里按照节1 中的设定(e =1mm)，并考虑CCD的影响，分别改变晶圆偏心量大小及初始转角进行仿真，得到结果如下。

(1)改变偏心量大小时的偏心识别。

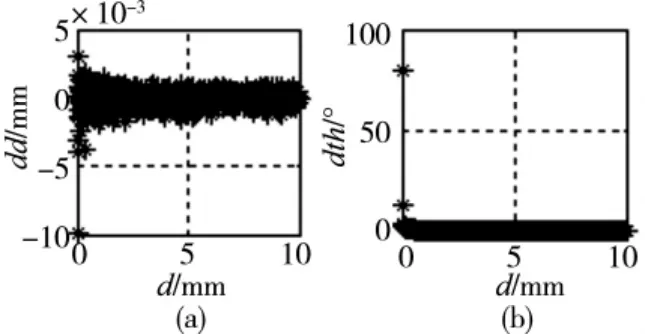
图7 改变偏心量大小时偏心的识别误差

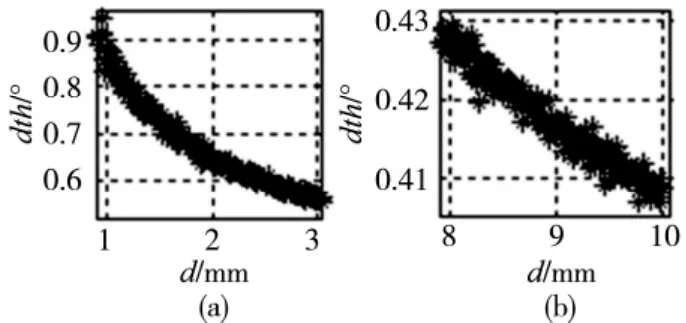
图8 改变偏心量大小时偏心角的识别误差

(2)改变初始转角时的偏心识别

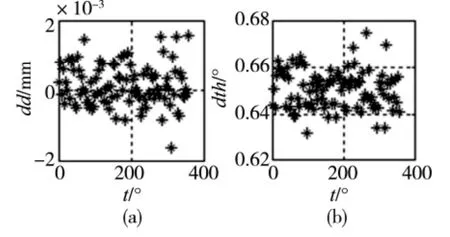
图9 改变初始转角时的偏心识别误差

2.3 不考虑CCD 影响时的偏心识别

仍按照1.2 中的设定，并且不考虑CCD 的影响，改变晶圆偏心量大小进行仿真，得到结果如图10。

可以看到，晶圆偏心量的识别几乎不受转动中心偏置的影响;晶圆偏心角的识别同时受转动中心偏置和CCD 的影响，并且大致成叠加关系;当综合考虑转动中心偏置和CCD 的影响时，随着晶圆偏心量增大，对其识别误差逐渐下降并趋于稳定;另外，虽然由于两项因素相叠加的关系使对偏心角的识别误差加大，但随着晶圆初始转角的改变(0 ～360°)，识别误差却保持了较好的稳定性，最大波动不超过0.05°也就是说，当晶圆的初始偏心量被控制在一定范围内(如8 ～10mm)时，并且在转动中心偏置及CCD 不变的情况下，不仅对晶圆偏心量的识别将会比较准确(误差在0.01mm 以内)，而且对晶圆偏心角的识别误差也会保持相对的稳定(波动在0.05°以内)。这对晶圆预对准误差的控制、标定及补偿等方面都较为有利。

2.4 晶圆缺口识别误差精度分析

对于晶圆缺口的识别采用较常见的一阶差分法［4-5］。当晶圆被准确对心后其边缘数据的一阶差分如图11 所示。

图11 晶圆边缘数据一阶差分

图12 为各参数对晶圆缺口识别的影响，其中图13a 为晶圆偏心量大小对结果的影响，可以看出，晶圆缺口识别误差与晶圆偏心量大小基本成正比，即偏心量越大误差也越大，因此，需要在晶圆对心后进行缺口识别。图12b 为转动中心偏置对结果的影响，与晶圆偏心识别相同，转动中心偏置对缺口识别的影响也可转化一角度偏差，且此偏差基本也偏心识别时相同，为0.3375°。图12c 为CCD 对结果的影响，它对结果造成了±0.08°的随机误差。图12d 为综合考虑以上各项因素时的晶圆缺口识别情况，对结果造成了0.18°至0.38°的偏差，有0.2°的波动，波动是由CCD 读数的随机误差造成的。其中，各影响因素的大小分别为:晶圆偏心量0.1mm，转动中心偏置(1，－120°)，线阵CCD 精度0.03mm。而晶圆初始转角对其缺口识别的影响与偏心识别类似，可忽略不计，这里不再赘述。

3 结论

基于晶圆预对准模型，通过将仿真得到的结果与设定值进行比较，得到了晶圆偏心及缺口识别的绝对误差，系统地分析了各因素对晶圆偏心及缺口识别的影响规律。得到的重要结论如下:

图12 晶圆缺口的识别误差

①采用精度在0.03mm 或更高的线阵CCD 传感器，晶圆偏心量的识别受转动中心偏置及晶圆初始状态的影响较小，在忽略其他因素影响时，其精度可达到±0.005mm;

②晶圆转动中心相对CCD 线阵所在直线的偏置对晶圆偏心及缺口识别的影响可转化为一固定的偏角，在本文所设定的条件下，其大小在0.33°至0.34°之间;

③当考虑CCD 的影响时，随着晶圆偏心量的增大，对晶圆偏心角的识别误差逐渐下降并趋于稳定;

④晶圆初始转角对晶圆偏心及缺口识别的影响较小，可忽略不计;

⑤当CCD 精度为0.03mm 时，其对晶圆缺口的识别会造成±0.08°的影响;

⑥晶圆缺口识别误差与晶圆偏心量大小基本成正比，即偏心量越大误差也越大，当偏心量在0.1mm以下时，此影响可忽略不计。

［1］Vladimir W. R. Volovich，San Jose. Semiconductor object pre-aligning method［P］. USA:5125791，1992－6－30.

［2］周杰，韩龙. 采用线阵型光学传感器的晶圆预对准方法［J］. 黑龙江科技学院学报，2009，19(6):465－469.

［3］乔遂龙. 嵌入式晶圆预对准控制系统的研究［D］. 哈尔滨:哈尔滨工业大学，2007.

［4］李春江. 晶圆处理预对准系统的研究［D］. 哈尔滨:哈尔滨工业大学，2006.

［5］荣伟彬，宋亦旭，等. 硅片处理预对准系统的研究［J］.机器人，2007，29(4):331－336.

［6］杜宇. 硅片预对准系统的研制［D］. 大连:大连理工大学，2006.