可伸缩中间轴主轴的强度和刚度计算

高龙，刘晟昱，冉振云

(中航工业株洲易力达机电有限公司，湖南株洲412002)

1 概述

这些年，电动助力转向系统 (Electric Power Steering，EPS)飞速发展，市场对于C-EPS 的操纵舒适性和可靠性的要求也越来越高。这种情况下，对高性能中间轴的需求也在不断增长，因此对高性能中间轴提出了以下要求:

(1)不会产生冲击力和异响(这直接导致在花键啮合时产生噪声，同时也严重降低了操作手感);

(2)有很好的刚性，保证其具有比较大的抗扭转刚度;

(3)具有很低的滑动负载(降低摩擦损耗);

(4)高寿命(要求反撞力能最低限度地增长，接触面的硬度能最低限度地降低)。

但是这都是建立在优良的强度和刚度的基础上，现在很多供应商厂家在主轴的结构设计工作有一定的滞后性，使得产品结构更新困难。图1 为某款中间轴样件性能曲线。

图中显示其抗破坏强度仅为210 N·m，刚度不到15 N·m/ (°)(而产品一般要求破坏强度不小于300 N·m，总成刚度不小于20 N·m/ (°))，对比图2 的批产合格件曲线图，很明显可以发现这是设计中的不足，由此可见，在主轴的定型生产加工前，强度和刚度的设计计算尤为重要。

2 强度计算

2.1 花键结构计算

通过扭转齿根剪切应力的计算推导出花键结构的基本尺寸范围和确定所选用的材料。

齿根弯曲剪应力:

材料的许用拉应力为［δ］，许用扭转剪切应力为［τ］，屈服极限为δs，强度极限为δb。对于塑性材料，［τ］ = (0.5 ～0.6)［δ］，通常情况下:

其中，n 为安全系数，n≥1。

考虑到通常试验检验要求为破坏强度大于等于Tmax，因此取δb用于计算。

花键齿根圆许用扭转剪切力

［τ］ =0.5δb(取n=1)

而τroot≤［τ］

则有

2.2 主轴强度计算

(1)抗扭截面模量Wt由轴的极惯性矩Iρ来确定

(2)对于复杂截面主轴的极惯性矩的计算则是分别计算每一结构的极惯性矩，然后再叠加计算。

主轴横截面如图3 所示，可将其视为实心花键轴和滑槽的布尔减运算结果，则其极惯性矩可表述如下:

式中:Iρ1为主轴实心轴极惯性矩;Iρ2为滑槽极惯性矩。

所以

式中:d 为分度圆直径。

而滑槽的结构简图如图4 所示。O1为主轴花键轴轴心，∠AO1C=β;O2为滑槽边线延长线和滑槽截面中心线交点，∠AO2C=α。则槽截面AEFC 的极惯性矩可表述为:

式中:Iρa是扇面AO1C 的极惯性矩;Iρb是三角形AO1O2的极惯性矩;Iρc是三角形EO2F 的极惯性矩。

于是有:

式中:d 为分度圆直径。

积分可得:

同理得:

在设计中采用取值代入法(建立参数数据库)，综合考虑以得到最适合的截面设计参数。

3 刚度计算

当分析一个阶梯轴或者花键轴的时候，将其分解成串联或并联的圆轴或花键轴单体，并确定每个单体的扭转刚度，然后求出总的扭转刚度。

(1)并联轴的总扭转刚度为各单体刚度的代数和:

(2)串联轴的总扭转刚度的倒数为各单体扭转刚度的倒数代数和:

3.1 圆轴

对于等直径截面圆轴:

故扭转刚度

3.2 花键轴

花键以及带有键槽轴的扭转刚度可用有限差分法求解圣维南扭转应力函数求出，得到函数方程:

其中，扭矩系数K 查图5 可得。

4 实例验算

以某款样件作为验算的参考件，如图6 所示。

4.1 强度的计算

(1)估算基本尺寸和材料的确定

而Tmax=300 N·m，加工前材料未做前期处理(如调质、正火等)提高强度。

①当使用20 号钢时，δb=390 MPa，得到Dmin=19.87 mm(可以做较大直径套筒)

②当使用35 号钢时，δb=510 MPa，得到Dmin=18.17 mm

③当使用20Cr 时，δb=834 MPa，得到Dmin=15.42 mm(可以做较小直径主轴)

(2)现在分度圆直径d =20.79 mm，槽底宽| EF | =2 mm，滑槽槽型角α = 83°，滑槽中心角β = 41.8°，代入式(5)— (11)得:

主轴花键轴部分

Iρ=1.436 0 ×10-8m4

主轴实心轴部分

而外花键齿根圆直径为19.8 mm，［τ］ =0.5δb，取35 号钢时有［τ］ = 255 MPa，即可满足要求。

套筒内花键部分

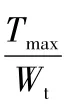
而内花键齿根圆直径为21.9 mm，［τ］ =0.5δb，取20 号钢时有［τ］ =180 MPa，即可满足要求。

4.2 刚度的计算

主轴花键轴部分B/R=0.075 8，远小于0.1，查表发现不适用，因此在这种模数很小的情况下，还是采用拟合计算的方法得到极惯性矩再计算刚度。

(1)C1是主轴实心圆轴部分的刚度，由式(12)可得

花键轴部分刚度

综合式(5)— (13)可得:

Iρ21=1.436 0 ×10-8m4

C21=35.900 ×103N·m/rad

C23=36.470 ×103N·m/rad

d=19.7 mm 时，代入式(11)得到:

Iρ22=1.086 4 ×10-8m4

故C22=72.427 ×103N·m/rad

得C2=14.476 ×103N·m/rad

CS=7.51 ×103N·m/rad (设计参考)

然后再得到套筒的各段刚度，以及万向节组合的刚度就可以计算出中间轴的基本刚度值。

(3)套筒分为三段，花键部分偶合段，花间部分非偶合段，尾部套筒段。它们对应的刚度分别是C31、C32、C33。由于套筒内部开有三道滚道，计算采用花键底径拟合运算其极惯性矩。

内花键部分

尾部套筒部分

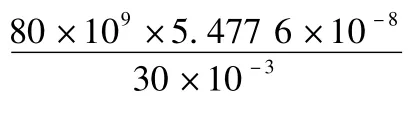
(4)可由结构并、串联关系求得中间轴除万向节叉组合的刚度CZ。

得到CZ=10.151 ×103N·m/rad =181.4 N·m/ (°)(有较大的刚度余量)

(5)由试验测试和相关计算显示中间轴万向节叉组合的刚度一般能达50 N·m/ (°) (万向节叉组合的刚度对整体刚度影响很大)。

故中间轴的总体刚度:

得到CS=21.97 N·m/ (°)，满足要求。

【1】ISAKOMER Robert I. Machine Design［M］. Torsional Rigidity of Composite Shates，1983.

【2】SOFRONAN T. Case 21:Analyzing a Spline Failure:Torsional Spline Failures are Telling you Something［J］. Hydrocarbon Processing，2004，83(6).

【3】UEDA h.Technical Trends Regarding Intermediate Shaft in Steering Systems［J］.Koyo Engineering Journal，2005，168.

【4】孙小伟.渐开线齿轮花键冷挤压工艺研究［D］.吉林:长春理工大学，2002.

【5】张兴旺. 花键冷滚压工艺与实验研究［D］. 山西:太原科技大学，2009.