UPQC 中串联逆变器的控制研究
李 强 ,李晓莉
(1.中铁21 局电务电化公司,兰州730030;2.兰州交通大学自动化与电气学院,兰州730070)
1 UPQC 简介
UPQC 的一个显著特性是一个典型的直流电容器(CDC)连接在电压源逆变器(VSI)两端,而不是一个直流电源。由于串联补偿器和并联补偿器都是无损的,需要一个特殊的直流环节电压控制器来使直流侧电容电压的平均电压保持恒定。在UPQC 中,并联补偿器通常负责这一电压的调节。在稳定状态,直流侧电压保持在设定值,但在暂态情况下不是这样的。暂态发生在当负载与UPQC连接、断开或电源电压跌落、上升的期间。因为计算新的参考电流需要一定的时间,所以并联补偿器不能及时反映负载的变化。此外,一些时间的设定围绕着稳定控制参数的参考值。因此,在负载变化的瞬间,通过直流侧电容器上的平均电压与他的参考值之间存在一段过渡时间。图1 为UPQC 的系统结构框图。
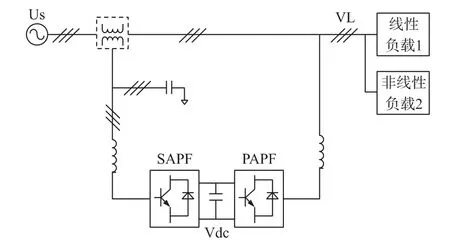
图1 UPQC 系统的结构框图
2 串联变频器控制
为了使输出交流电压波形接近正弦波,采用多种方案来调制串联逆变器的开关频率。文献[6]所详述的正弦脉宽调制方案被广泛应用。在该方案中,通过模数比较器来比较正弦波(控制信号)和三角波(载波信号)进而产生开关脉冲。调制深度ma可定义为:

当Vcontrol为调制信号的幅值,Vtri为三角波信号的幅值时,调制深度通常保持恒定。
电压源逆变器输出电压基波分量的幅值取决于直流侧输入电压和调制深度:

在典型应用中,逆变器的输出电压通常保持常数。对于确定的Vout(1),对应的ma可从式(2)中计算出,再由式(1)算出Vcontrol。假定Vdc恒定,为使Vout(1)在一定时间内恒定,ma必须保持恒定。然而,如果ma在某时间段内保持不变,而Vdc偏离其参考值,则Vout(1)也会偏离预设值。如果要求Vout(1)恒定,但Vdc偏离参考值,则ma必须作相应调整。因此,在这里建议,暂态时串联逆变器的正弦脉宽调制的调制深度必须不断调整以匹配直流侧实际电压Vdc·act,而不是采取参考直流侧电压。由式(1)和式(2)得调制信号的幅值为:

Vdc=Vdc·ref时,由于Vtri和Vdc·ref是常数,则Vcontrol是只有一个变量Vout(1)的函数。因此,无论在稳态和暂态时出现实际直流侧电压偏离其参考值时都不影响Vcontrol,且对于特定的Vout(1),Vcontrol的幅值是固定的。
为使Vcontrol对应直流侧电压的变换,将Vdc=Vdc·act代入式(3),则Vcontrol是关于Vout(1)和Vdc·act的双变量函数。由于任何直流侧电压偏差对Vcontrol都有直接影响,故Vcontrol的计算是连续进行的。因此,当直流侧电压发生上升或跌落时的瞬间,调制信号的幅值会相应调整且串联逆变器输出电压的基波分量幅值仍不受偏差影响。故无论在稳态还是暂态,该串联补偿器都能够注入适当电压使负载侧电压幅值保持在理想水平[8]。
这种复制能力与变革能力从哪里来?这就是管理要思考的首要命题。企业在小的时候,在业务模式没有起来之前,要探索可复制能力,一定要形成经验,应用到更大、更广的范围,管理首先是对经验的管理。例如:有十个业务人员,一定要将其中资历深的业务人员的成功经验形成工具、方法,复制到新人身上。经验被放大后,在一个店能做成功,也能复制到更多的店获得成功,往更大的范围去做,企业也能变得更大。
调制深度通常保持在线性范围内,电压的基波幅值随ma线性变化。若进一步增加输出基波电压幅值使调制深度大于1.0 就会导致系统超调。超调导致逆变器的输出电压含有更多低次谐波。更重要的是,超调时的基波分量幅值不再与调制深度呈线性关系。当ma足够大时,逆变器将退化到方波逆变的工作状态。因此,在超调区内,逆变器的输出电压基波分量的幅值为[6]:

考虑到式(2)中Vdc=Vdc·act,则调制深度为:

为保证逆变器工作在线性区,必须满足以下条件:

由于超调,逆变器输出电压的基波分量幅值相比线性调制模式最大可能值增加了27.32%。它也可以总结为逆变器输出电压Vout(1)的基波分量的幅值不低于直流侧参考电压的78.54%。因直流侧电压低于该值则逆变器输出电压的基波分量的幅值低于Vdc·ref/2,这似乎是出现严重电源电压跌落的条件,因此应当避免Vdc<0.785 4Vdc·ref的情形出现。
用于计算调制深度的式(5)可改写如下:


UPQC 的串联逆变器通常运行在线性调制模式且按照此条件设计。该逆变器在线性调制模式下的输出电压基波分量的最大值Vout(1)max=Vdc·ref/2,此值对应于调制深度ma·ref=1。在稳态下,实际直流侧电压Vdc·act不仅有波动且包含直流和交流成分。由于直流侧电压控制器,直流侧电压保持恒定且等于Vdc·ref。在交流分量处于负值的时间段,实际的直流侧电压Vdc·act比Vdc·ref小,且Vdc·ref/Vdc·act>1。因此可以从式(7)看出,当ma·ref=1且Vdc·ref/Vdc·act>1时,调制深度ma>1,这使得逆变器运行在非线性模式,因此逆变器的输出电压中出现谐波。如果在稳态时,式(7)的调制深度大于临界值,那么它应该等于常规调制深度ma=ma·ref。
综上述,设串联逆变器满足以下条件和控制规则:
(1)若直流侧电压偏离其参考值Vdc·ref大于最大稳态纹波,则式(7)可作为系统在暂态时的调制深度的计算公式。
(2)系统处于稳态且调制深度不大于临界值时,可使用式(7)计算调制深度ma。
(3)如果系统处于稳态,且根据式(7)中的ma>1,则ma等同于常规调制深度ma=ma·ref。
(4)当Vdc<0.785 4Vdc·ref时导致串联逆变器的输出电压的幅值低于Vdc·ref/2,可通过选择合适的直流侧电容容量和设计直流侧电压控制器来避免此情况出现。
3 仿真结果分析
将以上所提出的控制策略通过MATLAB 进行仿真验证,该仿真系统建立在12 kVA 的试验平台上,电源相电压为230 V,直流电容器CDC=2 000 μF,滤波电感L=1.245 mH,仿真结果如下所示。该干扰由电源电压跌落到50%和UPQC 在2 s 和3.5 s 时连接和断开负荷所致。图2 显示了直流侧电压变化情况。
直流侧电压参考值设定为400 V,从图2 中可看出,UPQC 在2 s 时接入全负荷导致直流侧电压跌落(约50%)。由于直流侧电压控制器的作用,直流侧电压在2.5 s 恢复到其参考值。在3.5 s 时负荷从UPQC 中断开,产生一个大的过电压(约50%)通过直流电容器,同样由于直流电压控制器的作用,扰动在3.8 s 时消失。

图2 直流侧电压波形
图3显示串联逆变器注入电压的两种情形。为了使负载侧电压达到额定值(相电压230 V),串联变换器必须注入115 V。从图4(a)可看出,稳态时串联变换器注入所需电压。在2 s ~2.5 s 和3.5 s ~3.8 s 期间,直流侧电压偏差和ma保持常数使得串联逆变器注入电压不合适,导致负载电压在此瞬间出现偏差。在第1个瞬间(2.0 s ~2.5 s),负载电压降到170 V(额定值的74%),在第2 个瞬间(3.5 s ~3.8 s),负载电压上升到300 V(额定值的131%),如图4(a)所示。

图3 ma 不同取值下的注入电流
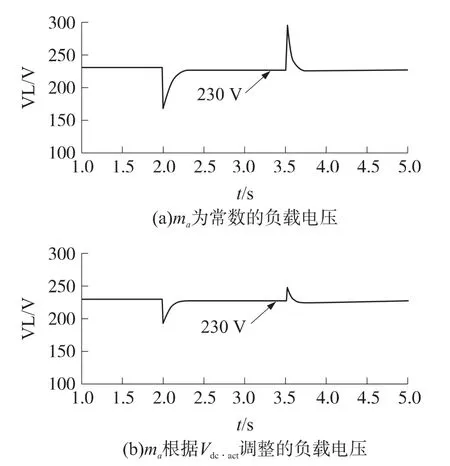
图4 ma 不同取值下的负载电压
图3 (b)和图4(b)分别显示的是串联注入电压和负载电压在根据Vdc·act不断调整ma的情形下的图形。从这些图中可以看出,在第2 个瞬间的电压偏差是微不足道的。
4 结论
通过分析UPQC 串联变频器正弦脉宽调制的调
制深度在不同范围内的取值,得出了逆变器输出电压的基波幅值随调制深度的变化关系。以此为基础,获得了串联逆变器输出电压的控制方法,即根据直流侧实际电压不断调整串联逆变器的调制深度,利用这种方法可以补偿电源电压的跌落、不平衡和失真。仿真结果表明,在电源电压和负载发生变化时,逆变器输出电压和负载电压都能保持稳定,串联逆变器具有较好的补偿效果,表明这种改进的正弦脉宽调制法是可行的。
[1] Rashid M H. Power Electronics Handbook:Devices,Circuits,and Applications,Elsevier,2007.
[2] Akagi H,Watanabe E H,Aredes M,et al. Instantaneous Power Theory and Applications to Power Conditioning[J].John Wiley &Sons,Inc.,2007.
[3] Akagi H. Trends in Active Power Line Conditioners[J]. IEEE Trans Power Electron,1994,9(3):263-268.
[4] Fujita H,Akagi H.The Unified Power Quality Conditioner:The Integration of Series-and Hunt-Active Filters[J].IEEE Trans Power Electron,1998,13(2):315-322.
[5] Ghosh A,Ledwich G. Power Quality Enhancement Using Custom Power Devices[M].Boston:Kluwer Academic Publishers,2002.
[6] Mohan N,Undeland T M,Robbins W. Power Electronics:Converters,Applications,and Design[M]. New York:John Willey& Sons,Inc.,1995.
[7] Basu M,Das S P,Gopal K,et al.Investigation on the Performance of UPQC-Q for Voltage Sag Mitigation and PQ Improvement at a Critical Load Point[J]. IET Gener Transm Distrib,2008,2(3):414-423.
[8] 梁祖权,束洪春,刘志坚,等. UPQC 完全解耦直接控制策略[J].电力自动化设备,2009,29(4):27-31.

