网络数据包传输占用缓存大小混沌特性分析

唐 红，胡 容，廖荣南

(重庆邮电大学网络与计算研究中心，重庆400065)

0 引言

互联网是一个规模巨大、难以控制的复杂网络系统［1］，已发现其拓扑结构具有无尺度特性［2］，节点度具有幂律分布特性［3－4］，流量具有自相似性［5］，在自治系统(autonomous system，AS)层面互联网具有富人俱乐部现象［6］，Internet业务量的多重分形特性［7－9］等一系列重要的复杂系统特性及现象，对互联网运行维护和管理控制带来严峻挑战。路由器是互联网中为信息流或数据分组选择路由的设备，是网络之间互连的枢纽。路由器缓存是分组交换网络的重要传输机制，在数据包传输过程中，路由节点的缓存占用情况也展现出各种复杂的网络行为，深入研究认识这些行为可以为新机制、新协议的设计及网络管理提供参考，具有重要的理论和工程意义。

袁坚等对网络内部节点的整体行为进行了探讨，发现各网络节点的缓存占用大小在时间和空间上均呈现幂律分布［10－11］，网络节点的整体行为表现出自组织临界现象［10］。刘锋等提出了一种描述计算机互联网络数据包传输的简单模型，并研究了沿着网络固定路径中路由节点数据包占用缓存大小的统计特性，研究结果表明系统存在自由流和拥塞流两种相态，在自由流状态，数据包占用缓存大小服从幂律分布，在拥塞状态，路由节点数据包占用缓存大小呈现白噪声特性［12］。还有研究结果表明，网络节点数据包占用缓存大小在时间序列上具有自相似特性，自相似程度呈现负相关;在功率谱图中具有幂律分布特性，在高频段呈现出白噪声特性［13］。这些研究结果表明，网络节点缓存占用大小分布具有复杂网络特性。

为了能更深入的研究缓存占用大小分布的复杂网络行为，考虑到互联网是无尺度网络这一特性，本文建立了一个无尺度元胞自动机模型，以互联网中实际运行的拥塞控制机制等作为元胞之间交互的规则，模拟数据包的传输过程，得到更为符合网络实际的缓存占用大小数据，然后通过计算Lyapunov指数对节点缓存占用大小的混沌特性进行分析。

1 基于无尺度网络的元胞自动机模型及仿真

1.1 仿真模型

元胞自动机是定义在一个由具有离散、有限状态的元胞组成的元胞空间上，并按照一定局部交互规则，在离散的时间维上演化的动力学系统［14］。元胞自动机模型最初主要用于生物、交通和地理信息系统等方面的动力学研究。近年来，元胞自动机模型也被应用到网络行为的研究，并且因其结构简单，容易在计算机上实现，能突现出宏观上的一些复杂行为，已经成为网络复杂行为的重要研究方法［15］。

大量的研究已证明互联网是无尺度网络，为了更为真实地模拟互联网行为，本文采用Barabási和Abert［16］提出的算法构建了一个无尺度元胞自动机模型，并将元胞分为核心元胞和普通元胞。

1)核心元胞:节点度超过10的元胞定义为核心元胞，与网络中核心路由器相对应。核心元胞只具有存储和转发数据包的功能。

2)普通元胞:节点度少于10的元胞定义为普通元胞，与网络中边缘路由器及与之相连的终端相对应，具有随机产生数据包和存储转发数据包功能。

每个元胞都具有一个缓存空间Cn，定义元胞单位时间内能处理数据包的最大个数为元胞的处理速度Vrouter。元胞的邻居是在无尺度网络中与该元胞有直接边相连的节点。t时刻某元胞的状态不但受当前时刻邻居元胞状态的影响，还受自己在前一时刻状态的影响。所有元胞在局部交互规则的作用下，相互协作完成数据包的传输。

1.2 交互规则

网络中路由器转发数据包的实际过程是:终端随机产生的数据包首先到达边缘路由器，路由器根据数据包携带的目的IP地址查看路由表，然后将数据包按照正确的端口转发到下一个路由器，经历过若干个中间节点，最终达到目的端。

根据这个过程，模型中的数据包通过一系列的元胞存储转发到达目的节点。元胞在为数据包进行路由选择时采取静态路由算法，即路由过程中即使发生了拥塞现象，元胞也不会再选择其他的路径。采用Floyd算法求出前述无尺度网络中任意两个元胞之间的最短路径并存储在每个元胞的路由表中。

模型中采用以下方式转发数据包:在每一时刻，按照先入先出的顺序取出数据包并根据路由表确定该数据包要转发到的下一个元胞，如果下一个元胞缓存已经饱和，则数据包在这一时刻停留在原来的元胞缓存队列中;如果没有饱和，则对数据包进行转发。

参照TCP拥塞控制机制，定义了元胞交互机制如下［13］。

1)t=0时刻，初始化每个元胞已占用的缓存队列qn，缓存队列大小为Cn，最大时步T。

2)由于真实网络中每时刻终端随机的产生一定数量的数据包，因此在每一时步每个普通元胞按照均匀分布方式产生数据包vterminal(t)，这些数据包把与该普通元胞直接相连的元胞作为源节点，其余元胞为目的节点的数据包，并排在该元胞缓存队列的最后面。元胞每步可以处理的数据包个数由路由最大转发速率Vrouter(n)和发送速率vn_out(t)决定，未得到处理的数据包在缓存队列中等待。

3)按每一时步，进行以下步骤。

第1步，每个普通元胞按照均匀分布方式随机产生n个数据包，其中1nM，M=50。

第2步，计算缓存队列大小。

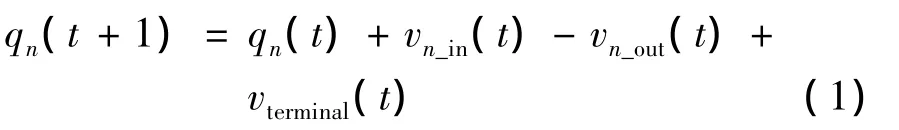
(1)式中:vn_in(t)为t时刻元胞n接收的数据包数量，等于所有邻居元胞在t时刻发送到该元胞的数据包总和;vn_out(t)为该元胞在t时刻发送出去的数据包总数。

第3步，判断每个数据包是否到达目的端，如果没有达到则该数据包生存时间加1。

第4步，计算每个元胞的最大发送速率vn_max(t+1)，规则如下。

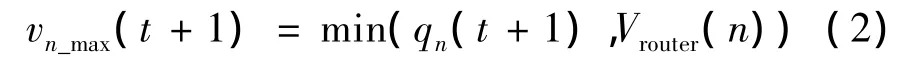
第5步，计算每个元胞的期望发送速率vn_expect(t+1)。

根据实际的拥塞控制机制，为发送速率设置一个门限值，该门限值设置为该时刻此元胞最大发送速率的一半vn_max(t)/2，如果vn_out(t)vn_max(t)/2，期望发送速率成指数级增长，类似于TCP拥塞控制算法中的“慢速启动”过程;当vn_max(t)/2≤vn_out(t)vn_max(t)时，说明网络已经快要达到饱和状态，应该以一个较小的增长速率a进行数据的发送，模型进入“拥塞避免”阶段，防止网络产生大量的丢包。当vn_out(t)≥vn_max(t)时，采用“快速恢复”策略，网络缓存队列已经发生拥塞，则马上调整网络的发送速率，设置一个减少系数b，用于控制发包速度，减少拥塞程度，规则如下

第6步，计算每个元胞的实际发送速率vn_out(t+1)

第7步，统计每一时步的丢包数，当生命周期到达时数据包都还没有转发到目的终端，则认为已经丢包，并把这个数据包从元胞的缓存队列中清除。

第8步，如果t小于时刻T，则返回第一步继续执行，否则退出。

1.3 仿真结果

采用无尺度网络模型，生成了一个有291条边和100个元胞构成的网络拓扑，其中有11个核心元胞和89个普通元胞。利用上述局部交互机制，应用元胞自动机模型进行数据包传输过程的仿真，缓存队列大小Cn=5 000，元胞处理速度vrouter(n)=500，为防止模型中在初始时刻内发生拥塞，设置数据包数量M=50，初始发送速率vn_out(t=0)=1，参数a=1，b=1/2，经过T=10 000步得到每一时刻元胞的缓存占用大小分布情况，总体上核心元胞的缓存占用比普通元胞的缓存占用多，但它们的分布都是随时间波动的，而在不同时刻，100个元胞的缓存占用大小的分布却是相似的。因文章篇幅有限，在所有元胞中随机选取了一个核心元胞和一个普通元胞的缓存占用大小随时间的分布情况如图1所示。

从图1中可以看出单个元胞缓存占用大小随时间波动比较大，核心元胞的缓存占用大小数值分布在100—430，普通元胞的缓存占用大小数值分布在20—150范围内，核心元胞缓存占用大小比普通元胞的更大，产生该现象的原因是核心元胞具有更多的邻居，每时刻流经核心元胞的数据包数量比普通元胞多。

为了观察不同时刻该模型中所有元胞的缓存占用大小的分布情况，取出第1 000，5 000和10 000时刻的数据，如图2所示，分别代表了整个过程的初始阶段，中间阶段和结束时刻，其中X轴为不同的元胞编号，元胞按照无尺度模型中加入的先后顺序编号。

图1 节点缓存占用大小Fig.1 Size of node＇s cache occupied

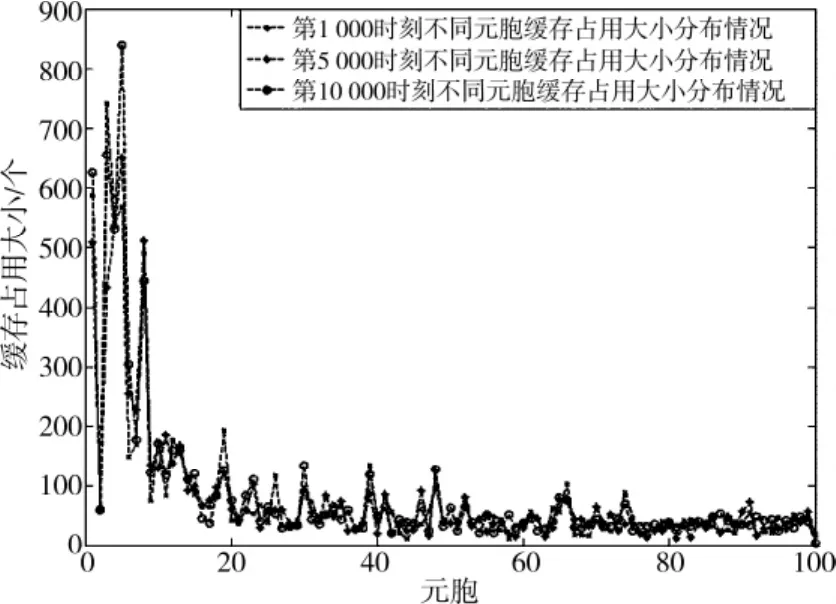
图2 不同时刻缓存占用大小分布图Fig.2 Cache occupied size distribution in different time

从图2中可以看出，在不同时刻，系统中元胞的缓存占用大小分布是相似的，系统处于稳定状态。为了验证这个直观结论，采用Lyapunov指数来对缓存占用大小的特性进行定量分析。

2 缓存占用大小的Lyapunov指数分析

Lyapunov指数是衡量系统动力学特性的一个重要定量指标，它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。Lyapunov指数沿某一方向取值的正负和大小，表示长时间系统在吸引子中相邻轨道沿该方向平均发散或收敛的快速程度，任何(平庸的和稳定的)吸引子必定有一个Lyapunov指数是负的;对于混沌，必有一个Lyapunov指数是正的，因此，只要由计算得知，吸引子至少有一个正的Lyapunov指数，便可以肯定它是混沌的。即对离散动力系统，或者说是非线性时间序列，往往不需要计算出所有的Lyapunov指数，通常只需计算出其最大的 Lyapunov指数即可［17］。1993年，Rosenstein M T等［18］提出了一种基于小数据集计算最大Lyapunov指数的方法。在此基础上，很多学者利用最大Lyapunov指数来分析系统的混沌性。由于基于无尺度元胞自动机模型中每一时刻每个元胞都不断的有新的数据包到达和离开，是一个由大量元胞相互作用的非线性复杂系统，因此我们采用Lyapunov指数来对占用的缓存大小的混沌特性进行分析。

采用Michael T.Rosenstein等提出的小数据量法［18］计算最大Lyapunov指数，具体步骤如下。

1)利用 Kim.H.S 等［22］1999 年提出的 C－C 算法计算时间延迟τ、嵌入维m。

2)求出功率谱及频率:Power=Y(1:N/2)2，f=(1:N/2)/(N);周期:period=1/f。

3)依计算时间延迟τ、嵌入维m重构相空间{Yj，j=1，2，…，M}。

4)找相空间中每个点Yj的最近邻点Y^j，并限制短暂分离，即

5)对相空间中每个点Yj计算出该邻点对的第i个离散时间步后的距离dj(i)

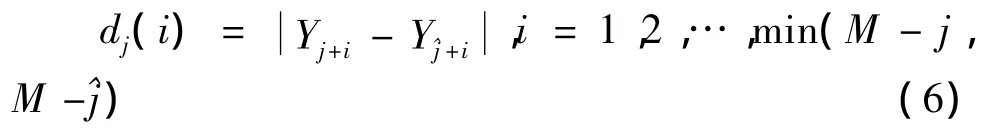
6)对每个i，求出所有j的dj(i)平均y(i)，即

7)用最小二乘法作回归直线，该直线的斜率就是最大Lyapunov指数。

3 实验和结果分析

3.1 单个元胞的缓存占用大小混沌特性分析

为了避免初值和过渡态的影响，取出图1所示的元胞缓存占用大小最后1 000个数据作为分析的基础数据，采用上节所述方法计算单个元胞缓存占用大小的最大Lyapunov指数，结果如下:计算普通元胞平均周期得到p=8.62(如图3所示)和最佳延迟 tau=3，时间窗tw=27，嵌入维m=10(如图4所示);计算核心元胞平均周期得到p=11.49和最佳延迟 tau=3，时间窗tw=16，嵌入维m=6.33。

曲线拟合求得普通元胞最大Lyapunov指数为0.007 1，如图5所示，核心元胞最大Lyapunov指数为0.003，如图6所示。

通过上面所示的流程及前面计算出来的最佳时延τ、最优嵌入维m及平均周期p，计算出单个普通元胞和核心元胞在本次实验中的最大Lyapunov指数分别为0.007 1和0.003，由上面介绍知道，最大Lyapunov指数为正数，便可以肯定它是奇怪的，从而知道单个普通元胞或核心元胞在不同时刻占用缓存大小变化是混沌的。

图3 计算平均周期图Fig.3 Calculating the average cycle

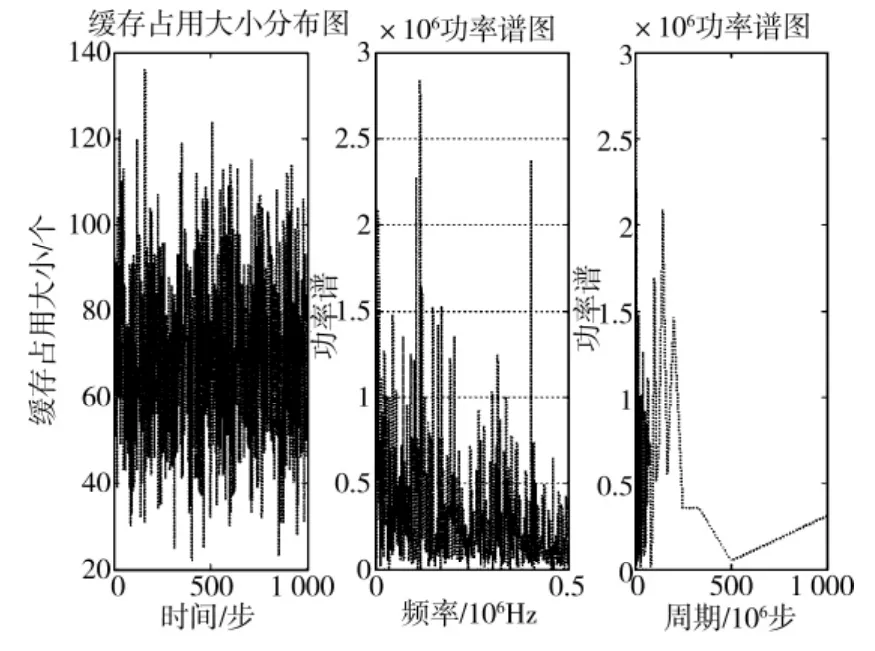
图4 最佳延迟，时间窗，嵌入维图Fig.4 Optimal delay，time window，embedding dimension

3.2 系统的缓存占用大小混沌特性分析

为了分析在不同时刻整个系统的缓存占用大小的混沌特性，采用图2所示的第1 000时刻、第5 000时刻和第10 000时刻所有元胞的缓存占用大小作为分析的基础数据。通过计算，在第1 000时刻曲线拟合求得最大Lyapunov指数为－0.822 84，如图7所示;在第5 000时刻曲线拟合求得最大Lyapunov指为－0.683 9，如图8所示;在第10 000时刻曲线拟合求得最大Lyapunov指为－1.183 1，如图9所示。

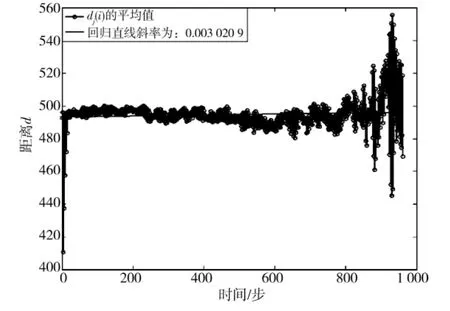
图6 核心元胞最大Lyapunov指数分布Fig.6 Most Lyapunov exponent distribution of kernel cell

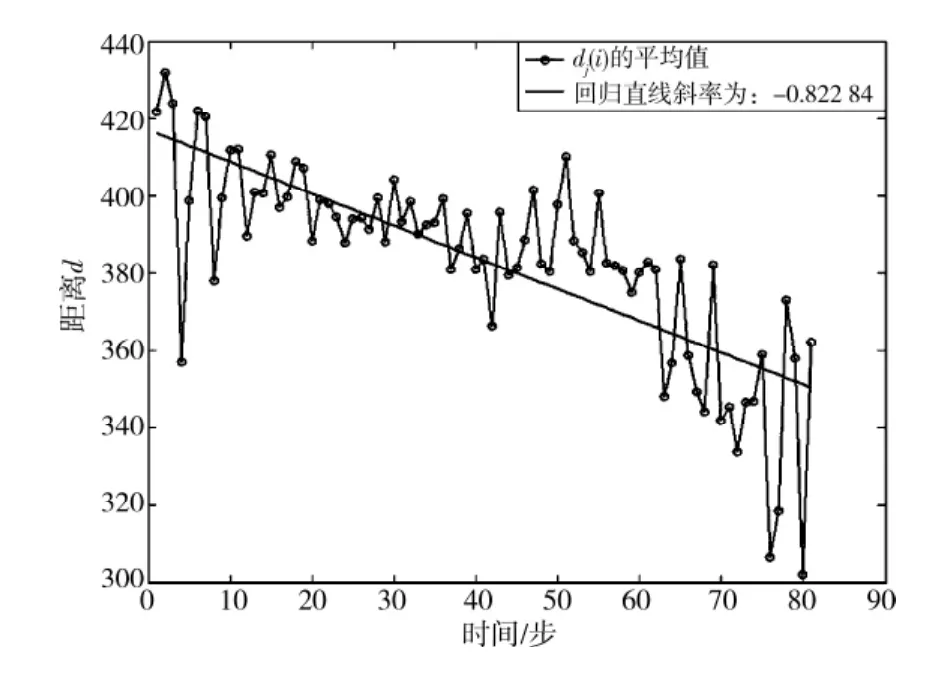
图7 第1 000时刻最大Lyapunov指数分布Fig.7 Most Lyapunov exponent distribution of the one thousand moment

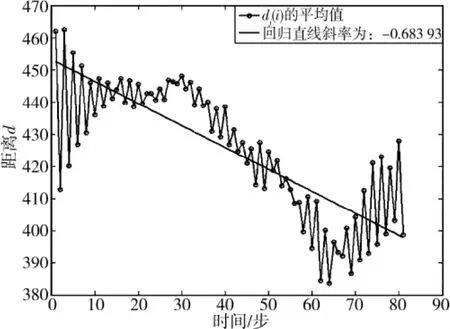
图8 第5 000时刻最大Lyapunov指数分布Fig.8 Most Lyapunov exponent distribution of the five thousand moment

通过分析在某时刻元胞之间的占用缓存大小的最大Lyapunov指数，发现在第1 000，5 000和10 000时刻所有元胞占用缓存大小最大Lyapunov指数均小于零，故可认为所有元胞构成的系统在不同时刻占用的缓存大小分布都比较均匀，系统处于稳定状态。这可以说明虽然单个元胞的缓存占用大小变化都是混沌的，但系统的缓存占用大小在元胞间相互作用下则处于稳定状态。

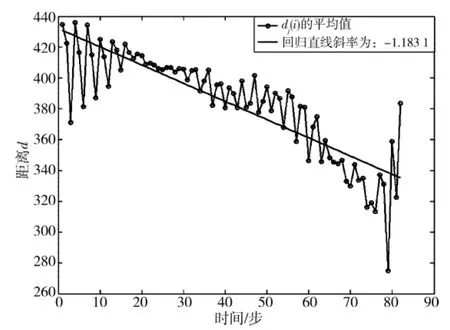
图9 第10 000时刻最大Lyapunov指数分布Fig.9 Most Lyapunov exponent distribution of the ten thousand moment

上面的计算和分析表明，网络中单个节点的缓存占用大小表现出不稳定的混沌特性，而所有节点构成的系统的缓存占用大小整体上则是稳定的。

4 结论

本文提出了一种无尺度元胞自动机模型，并引入拥塞控制等网络运行机制来更真实地模拟网络中数据包的传输;采用最大Lyapunov指数来定量分析单个节点及整体的缓存占用大小的混沌特性，发现单个节点的缓存占用大小是混沌的，而所有节点构成的系统的缓存占用大小是稳定的，这说明该系统是一个复杂系统，虽然其中的个体状态是不稳定的，但整体却突现出了稳定性。下一步工作可进一步通过最佳延迟，最佳嵌入维和最大Lyapunov指数来预测下一时刻节点的缓存占用情况，从而减少拥塞发生的概率，提高数据包传输效率。

［1］PARK K，WILLINGER W.The Internet as a large－scale complex system［M］.USA:Oxford University Press，2005:322.

［2］YASUHIRO Sato，SHINGO Ata，IKUO Oka.A strategic approach for re－organizing the Internet topology by applying social behavior dynamics［J］.Journal of Network and Systems Management，2009，12(1－2):208－229.

［3］MICHALIS Faloutsos，PETROS Faloutsos，CHRISTOS Faloutsos.On power－law relationships of the Internet topology［C］//In SIGCOMM＇99 Proceedings of the conference on Applications，technologies，architectures，and protocols for computer communication.USA:ACM New York，1999，29(4):251－262.

［4］GEORGOS Siganos，MICHALIS Faloutsos，PETROS Faloutsos，et al.Power laws and the AS－Level Internet topology［J］.IEEE/ACM TRANSACTIONS ON NETWORKING，2003，11(4):514－524.

［5］LELAND W E，TAQQU M S，WILLINGER W，et al.On the self－simlar nature of Ethernet traffic(extended version) ［J］.IEEE/ACM Transactions on Networking，1994，2(1):1－5.

［6］ZHOU S，MONDRAGON R J.The rich－club phenomenon in the Internet topology［J］.IEEE Communication Letters，2004，8(3):180－182.

［7］FELDMANN A，GILBERT A，WILLINGER W.The changing nature of network traffic:Scaling phenomena［J］.Computer Communication Review，1998.28(2):5－29.

［8］GILBERT A，WILLINGER W，FELDMANN A.Scaling analysis of random cascades，with applications to network traffic［J］.IEEE Transactions on Information Theory，1999，45(3):971－991.

［9］RUDOLF H，MATTHEW S，CROUSE V，et al.A multifractal wavelet model with application to network traffic［J］.IEEE Transactions on Information Theory，1999，45(3):991－1018.

［10］袁坚，任勇，山秀明.一种计算机网络的元胞自动机模型及分析［J］. 物理学报，2000，49(3):398－402.YUAN Jian，REN Yong，SHAN Xiuming.Investigation of a cellular automation model for computer network［J］.Journal of Physics，2000，49(3):398－402.

［11］TANG Hong，WANG Ying，WANG Haitao.A network emergent computing model based on cellular automaton［C］//Sixth International Conference on Network and Parallel Computing.US:IEEE Computer Society，Oct 2009:240－245.

［12］刘锋，任勇，山秀明.互联网络数据包传输的一种简单元胞自动机模型［J］.物理学报，2002，51(6):1175－1180.LIU Feng，REN Yong，SHAN Xiuming.A simple cellular automata model for packet transport in the Internet［J］.Journal of Physics，2002，51(6):1175－1180.

［13］唐红，廖荣南，胡容.无尺度网络的数据包传输元胞自动机模型研究［J］.计算机应用研究，2010，27(12):4686－4689.TANG Hong，LIAO Rongnan，HU Rong.Cellular automata model for packet transmission on scale－free network［J］.Application Research of Computers，2010，27(12):4686－4689.

［14］WOLFRAM S.Cellular automata as models of complexity［J］.Nature，1984，10(311):419－424.

［15］贺正求，贺建民，张叶琳.一种自组织的二维元胞自动机网络模型及分析［J］.计算机应用，2007，27(6):1330－1333.HE Zhengqiu，HE Jianmin，ZHANG Yelin.Analysis of a self－organized network model based on two－dimensional cellular automation［J］.Computer Applications，2007，27(6):1330－1333.

［16］BARABÁSI A L，ABERT R.Emergence of scaling in random networks［J］.Science，1999，286(5439):509－512.

［17］苏捷.基于Swarm的突现计算模型仿真及挖掘［D］.重庆:重庆邮电大学，2009.SU Jie.The simunation and mining based on the emergent computation model of Swarm［D］.Chong Qing:Chongqing University of Posts and Communications，2009.

［18］ROSENSTEIN M，COLLINS J，LUCA C，et al.A practical method for calculating largest lyapunov exponents from small data sets［J］.Physical D，1993，65(1－2):l17－134.

［19］CHEN Xiaoyu，LEI Humin.Study of lyapunov exponent of the chaotic signal wave interception［C］//In ICECE＇10 Proceedings of 2010 International Conference on Electrical and Control Engineering.USA:IEEE Computer Society，Jun 2010:2039－2042.

［20］CHEN A，LIU Jingjing.Identification of chaotic characteristic of power load based on lyapunov exponents［C］//2009 Second Asia－Pacific Conference on Computational Intelligence and Industrial Applications.US:IEEE Computer Society，2009:461－463.

［21］MARTINEZ F，GUILLAMON A，ALCARAZ J，et al.Detection of chaotic behaviour in speech signals using the largest lyapunov exponent［C］//14th International Conference on Digital Signal Processing，US:［s.n.］，2002:317－320.

［22］KIM H S，EYKHOLT R，SALAS J D.Nonlinear dynamics，delay Times，and embedding windows［J］.Physica D，1999，127(1－2):48－60.