高速移动环境下基于OFDM的LTE系统ICI 消除技术综述

李 丹，柯 峰

(1.韶关学院计算机科学学院，广东韶关512005;2.华南理工大学电子与信息工程学院，广东广州510640)

0 引言

近几十年，移动通信经过了几代技术革新，可提供的数据传输速率不断提高［1］。以正交频分复用(orthogonal frequency division multiplexing，OFDM)为核心的长期演进(long term evolution，LTE)移动通信系统的下行速率达100 Mbit/s，可支持高速率宽带多媒体业务。与此同时，终端的移动速度也随着高速铁路、公路的发展不断提高。目前，我国高铁列车平均时速超过250 km/h，最高时速达350 km/h。如何为高速移动的用户提供可靠的高速率数据通信，即“双高”问题［2］是LTE系统面临的难题。

LTE采用基于OFDM的空口技术，以提供更高的数据速率和频谱利用率。但在高速移动环境下，信道快速时变导致接收端受多普勒频偏影响，子载波间的正交性被破坏，形成子载波间干扰(inter－carrier－interference，ICI)，恶化系统性能。本文就这一问题，归纳总结了现有OFDM系统的ICI消除方法、存在问题及最新研究进展。报道了针对LTE系统的相关研究，并对今后研究工作提出展望。

1 移动环境下时变信道的多普勒频偏

多普勒频偏是由收发信机相对运动或路径中的物体移动引起的，在移动通信中通常是由终端移动引起。多普勒频偏在时域上表现为信道时变。终端移动速度越快，多普勒频偏越大，信道时变越剧烈。多普勒频偏fd的计算式为［3］

(1)式中:fmax为最大多普勒频偏;fc为载频;c为光速;v为终端移动速度;θ为入射角;λ为电磁波波长。

在陆地移动通信系统中，多普勒频偏通常为一段范围内的频偏扩展。因为，无线信道中电波的传播通常由许多路径来的反射、散射与绕射波合成。实际信道的反射表面相对波长多为粗糙表面，反射能量散射到所有方向，接收端收到的每一径信号一般为一些时延近乎相等的、不可分解的散射波的叠加［3］。根据 Parsons和Bajwa提出的椭圆模型［4］，接收端收到位于以发射端和接收端为焦点的椭圆上的所有散射体散射信号的传播时延相等。因此，接收端收到的每一径信号都是同一散射圆上一些不可分解的散射信号组合而成，表现出一径的瞬时幅度与相位。但位于同一散射圆的不同散射信号到达接收端的入射角不同，由收发端相对运动引起的多普勒频偏不同。因此，当发射单一频率f0信号时，接收信号的频谱为包含频率为f0－fmax～f0+fmax的频谱分量。

2 LTE及其在高速移动环境下的ICI

本节介绍LTE的特点及其空中接口物理层传输技术，并分析高速移动环境下LTE系统ICI的成因，以便于从根本上寻求LTE系统的ICI消除方法。

2.1 基于OFDM的LTE宽带移动通信技术

3GPP(the 3rdgeneration partnership project)EUTRA(evolved universal terrestrial radio access)长期演进，简称LTE。是3G移动通信向4G的演进，可支持的最高车速为350 km/h，甚至在某些频段最高可支持500 km/h。该标准于2004年底提出，2008年完成了第一个版本R8的制定。2010年的R10［5］版本是 LTE的平滑演进，被称为 LTE－Advanced，3GPP将其作为4G的首选技术。

LTE/LTE－A物理层以 OFDM为核心。OFDM凭借其抗多径能力强、频谱利用率高、均衡复杂度低等优点成为宽带无线通信的关键技术。正交频分多址接入(orthogonal frequency division multiplex access，OFDMA)是基于 OFDM的多址方式，在继承OFDM优点的同时又可根据信道特点及用户需求灵活地将不同数目、位置的正交子载波集分配给用户，充分利用了频率分集与多用户分集，是LTE下行的主流接入技术。由于OFDM(A)具有较高的峰均比，对功率放大器的要求较高，因此，LTE上行链路采用单载波频分多址接入(signal－carrier frequency division multiple access，SC－FDMA)［6］。通过将 OFDMA的输入进行离散傅里叶变换预编码，使输出具有单载波特性，降低上行发射终端输出的峰均比，减小终端的体积和成本。SC－FDMA预编码后的处理过程与OFDMA相同［6］，如图1所示。

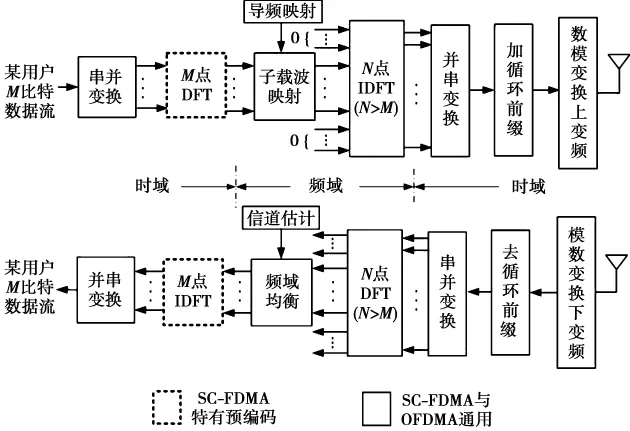
图1 OFDMA与SC－FDMA收发信号系统框图Fig.1 System diagram of OFDMA and SC－FDMA

2.2 高速移动引起的ICI

OFDM/OFDMA各个子载波之间要求严格正交，高速移动引起的多普勒频偏及载波频率的偏移等将使系统子载波之间的正交性遭到破坏，导致ICI［7］。本文仅对高速移动环境下，信道快速时变引起的多普勒频偏及其对系统造成ICI进行讨论与分析。载波频偏等引起的ICI不在本文研究范围之内。

为区别其他移动信道，本文研究的高速移动信道是指当移动性增加至信道在一个符号内发生时变的快变信道环境。此时，信道时域响应函数在一个符号间隔内为时间、多径的二维函数，写为h(n，l)，其中:0≤n≤N－1，n代表一个符号内的时间采样点，N为一个符号内的采样点总数;0≤l≤L－1，l代表多径采样点，L为最大多径采样点。信道频域矩阵G为非对角阵，其第m行n列元素表示为［8－9］

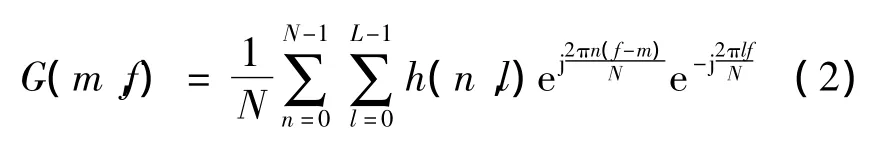
接收端，第m个子载波的信号表示为［7］

(3)式中:W(m)，X(m)分别为子载波m上的噪声与数据。由(2)式，当h(n，l)在一个符号内随时间采样点n变化时，子载波f对m的ICI干扰系数项不为零。此时，(3)式中f)X(f)项非零，从而引入ICI。因此，高速移动场景下，信道在一个符号内的时变是使OFDM系统引入ICI的根本原因［8］。

研究表明:1%的多普勒偏移造成的ICI功率水平为－30 dB［10］。当多普勒频偏增大，ICI功率水平大于噪声功率，单纯地将ICI当成噪声会使系统产生较大误码率平底［10］。通过频偏估计与补偿［11－12］只能粗略估计最大多普勒频偏 fmax，无法估计－fmax～fmax范围内的所有频偏分量，残余的频偏仍会造成ICI。

3 OFDM系统的ICI消除方法

自1996年起，国内外学者开始考虑高速移动环境下，信道在一个符号内时变引起的多普勒频偏对OFDM系统造成的ICI影响，提出了各种ICI消除方法，保证尽可能正确地恢复发送数据。

3.1 编码自消除

编码自消除的方法是通过数据编码抵消相邻子载波干扰的方法。Zhao Y［13］于1996提出在OFDM系统中利用多项式编码可大大抵消多普勒频偏引起的ICI，根据多项式权重将数据调制到相邻一组子载波，多项式阶数越高效果越好，但频带损失较大。Zhang H等［14］提出频带效率较高的频域部分响应编码方法消除多普勒频偏引起的ICI。此类ICI编码自消除方法在很大程度上消除了来自相邻子载波的主要ICI分量，但无法去除来自所有子载波的ICI。

3.2 均衡与迭代判决反馈消除

由2.2节的分析可知，ICI是由信道在一个符号内的时变引起。均衡就是利用信道估计信息，消除信道符号内时变对发送数据造成的ICI影响，从接收信号中恢复发送数据的过程。1999年Jeon W G［15］提出一种均衡消除ICI的方法，限定信道在一个符号内线性时变，其频域矩阵的ICI能量集中在对角线附近，忽略其余的微小ICI分量，从而通过简单矩阵求逆实现均衡去除 ICI。2001年，Choi Y S［16］提出了连续检测的最小均方误差均衡算法(SDMMSE)，复杂度为 O(N2)。2002 年，Cai Xiaodong［9］只考虑相邻有限子载波的ICI影响，提出了复杂度为O(N2)的判决反馈最小均方误差联合并行干扰消除的迭代算法。Stamoulis A［17］利用时域滤波抵消时变影响，使得信道频域矩阵为对角阵，从而实现一阶简单均衡去除ICI，复杂度为O(N)。以上均衡方法是去除ICI的有效方法，但需利用已知导频进行信道估计，事先获得信道状态信息［15－17］。

考虑到上述方法需要事先估计得到信道状态信息来实现均衡，复杂度也仍然较高。Schniter P［18］提出一种无需获得信道估计信息、复杂度仅为O(N)的迭代判决反馈检测数据的方法，利用时域加窗预处理将ICI限定在相邻有限个子载波，通过判决检测数据，同时计算最大信干比并反馈调整窗函数参数，经过多次迭代来消除ICI。当ICI严重时，其迭代的次数和计算量较大。

综上，利用信道信息进行均衡是去除高速移动信道ICI、正确恢复发送数据的根本方法。但前提要求通过信道估计获得良好的信道状态信息［15－17］。即，在高速移动的快变信道下，根据(3)式的向量形式［16］:由接收信号向量Y正确恢复发送数据向量X，只有利用已知的导频估计出信道时域响应函数h(n，l)在一个符号间隔内的时变特性，从而由(2)式得到信道频域矩阵G，才能通过求逆及判决等均衡过程彻底消除信道时变引起的ICI，正确恢复发送的数据向量 X［8，15－17］。因此，如何进行信道估计获得信道在一个符号内的时变及其频域矩阵的非对角线元素是均衡去除ICI的关键，也是研究的热点。

3.3 时域快变信道估计

对于OFDM系统快变信道估计的研究集中在2000年之后。主要思路是利用OFDM系统每个符号内插入在特定子载波上的已知导频符号估计信道时域响应各径在一个符号内的时变，从而得到频域响应矩阵的估计值，再通过均衡消除ICI。

由(2)式可知，对于在一个符号内时不变的信道，信道时域响应函数h(l)只有L个未知参数。对于快变信道，信道时域响应函数h(n，l)在一个符号内随时间变化，待估计的参数为L×N个。系统一个符号内频域子载波总数为N＜L×N，即使所有子载波都发送导频也无法准确估计所有未知参数。

Tsatsanis MK与Giannakis GB指出［19－20］:对于多径是由少数几个主要反射物引起的陆地移动通信无线信道，信道各径时变具有一定的周期性，其时变系数可由几个基函数的线性组合来表征。这种确定的基扩展模型将信道在一段观测时间内的时变估计转化为对该时间内时不变的基系数的估计。若信道最大多径抽头数为L，信道在观测时间内时变拟合模型基的阶数为Q(Q＜N)，采用基扩展模型拟合信道时变，可将待估计的参数由L×N个降至L×Q个。文献［8，15，17］利用线性基模型拟合信道各径在观测窗内的线性时变，估计参数大大减少。当车速较高时，非线性基扩展模型(BEM)可以较好拟合信道［20－27］。常用的基函数有多项式基［21］、KL基［22］、DPS基［23］、复指数基［20，24－25］等。多项式基的频域不具有带限性，多普勒频偏较小时，性能较好［25］，当多普勒频偏较大时，需要较高的阶数才能实现精确拟合［21］。对于其他具有频域带限特性的基函数，KL－BEM基在均方误差意义上是最优，但需要利用预先统计获得的信道的多普勒功率谱函数［22，25］，当先验信道统计特性与实际信道失配时，性能不再最优。DPS－BEM基采用一系列频域带限、时域功率近似集中在观测区间内的离散Prolate序列作为基函数。其基序列个数有限，获得较复杂［23，25］。CE－BEM 用一系列复指数函数作为基函数，实现简单，但拟合误差较大。改进的 GCEBEM［24］是 CE－BEM 的过采样，具有较好的拟合性能，但受Gibbs效应影响，其符号首尾边界拟合误差较大。一种改进的 CE－BEM［26］及基线补偿的BEM［27］可进一步降低 CE－BEM 及 GCE－BEM 的符号首尾边界拟合误差。图2、图3分别是对不同BEM基的快变信道估计性能的数值仿真结果［25－26］。图2假定信道先验知识与信道模型参数匹配。图3假定已知的归一化多普勒频移fn=0.5(fn=fmaxTs，Ts为一个符号间隔)，对比了信道模型参数与实际信道不匹配的情况下，不同BEM基的估计误差。

图2 不同BEM模型误差对于验证［25］Fig.2 Justification of BEM［25］

图3 不同BEM模型的展开均方误差与fn关系［26］Fig.3 MSE of BEM vs.fn［26］

对于快变信道估计，用于信道估计的梳状导频本身也会受到相邻未知数据子载波的ICI干扰。这部分干扰与高斯噪声不同，可通过控制数据及导频分布来降低。文献［9］提出导频等间隔分组分布可以隔离降低未知数据子载波对导频造成的ICI污染，提高估计性能。之后，文献［25］等也采用这种导频形式。因此，通过合理的导频设计或数据编码等方法可以将导频所受的ICI干扰降低至理想范围，保证信道估计的精度。

在高速移动环境下，利用上述基扩展模型拟合信道时域响应前L个采样点的时变特性，只要观测时间内的可用导频子载波数Np＞L×Q，即可实现对信道时域响应未知参数的估计，从而得到信道频域矩阵。我们称这类方法为OFDM时域快变信道估计方法。上述时域估计方法利用多径信道时域响应函数能量集中在前L个采样点内的低通性，当导频在频带内等间隔均匀分布时［8，17，25］，可获得高斯白噪声信道下的最小均方误差解。

研究表明:上述算法在理论上可获得最优解，但无法应用于实际系统。在实际OFDM系统中，通过导频估计的信道时域响应能量通常会泄漏到前L之外的所有样点，造成估计的误差平底［28－30］。因为实际的信道多径时延不可能刚好为采样间隔的整数倍，称为非整数倍采样信道［28］。文献［28－29］分析并给出了非整数倍采样信道下，利用导频估计值经傅里叶变换到时域得到的信道时域响应的归一化表达式。此时，信道时域响应函数非整数径的能量将泄漏到周围的所有采样点，其低通特性被破坏。2径整数倍采样信道 h(l)=δ(l－Ts)+0.5δ(l－4Ts)及非整数倍采样信道 h(l)=δ(l－1.5Ts)+0.5δ(l－4.5Ts)的时域响应函数，如图4所示。

图4 非整数采样信道的能量泄露Fig.4 Energy leakage of non－sample－spaced－channel

由能量泄露造成的估计误差将导致系统性能的“地板效应”［28－30］。文献［28－30］分别针对能量泄露的问题提出了改进的时域处理方法，如通过选取合适的L值、加窗迭代、对称扩展等降低能量泄露的影响，无法在根本上消除或避免能量泄露的影响。并且，以上研究均针对平稳信道，对于信道在一个符号内时变的快变信道估计方法未予考虑。

3.4 频域快变信道估计

针对OFDM时域信道估计能量泄露的问题，邝育军等［31］推导得出结论:对于OFDM系统，不变换到时域，只在频域利用导频进行信道估计的性能不受能量泄露影响。因为，信道的多径时延功率谱特征已经完全反映在信道频谱上，通过导频进行估计与插值可得到信道全频域响应。其估计误差仅与导频数目、间隔及噪声功率有关，与能量泄露无关。上述研究只针对平稳信道，并未考虑时变信道，但其研究结果为解决OFDM时域快变信道估计受能量泄露影响无法实用的问题提供了思路—在频域实现快变信道估计。

在此基础上，文献［32］提出基于 CE－BEM的OFDM频域快变信道估计方法。利用频域时变传输函数辅助估计得到信道频域矩阵。整个估计过程都在频域进行，不经过变换域处理。估计性能只与导频的分布间隔密度、基扩展模型的拟合误差及信噪比有关，避免了信道时域响应能量泄露的影响，适用于实际系统。

4 LTE快变信道估计去除ICI的研究现状及展望

基于OFDM的LTE系统，在高速移动环境下同样将受信道时变影响，产生ICI。本节重点针对LTE系统的ICI消除技术进行介绍，并对进一步研究的问题提出展望。

4.1 LTE系统快变信道估计

不同于单用户OFDM系统，LTE上下行链路均为多用户频分多址接入。各用户只占用频带内部分子载波集，各用户与基站的通信随机，信道估计要分别进行。假定用户数目为U，其信道估计参数是OFDM系统的U倍。

由于接收端收到的信号是各用户在时域上经历各自不同信道衰落后的叠加信号，很难分离。而在频域上分离相互正交的用户子载波集合非常容易。因此，通常在各用户子载波集合内插入导频，用于各用户的信道的估计与均衡［5］。对于下行OFDMA，如果不论各子载波集内用户是否发送数据，均在整个频带内发送公用导频，其信道估计方法与单用户OFDM类似。但如果只在有数据发送的用户子载波集内发送导频，则各用户只能利用其子载波集内的有限个导频实现估计。对于上行SC－FDMA，为了保证单载波特性，用户数据集中分布。为了不破坏数据的集中性，数据中将不插入导频子载波。因此，其导频不是OFDM系统常用的梳状导频，而是块导频。将时域上有一定间隔的特定符号作为导频［6］，各用户的导频通过频分或者码分方式复用。

因此，对于LTE频分多址接入系统，各用户可用导频资源(数目、能量)相对单用户OFDM成倍减少，且导频只能分布在可用的子载波集合内。

现有的大部分LTE的信道估计方法均在频域利用用户子载波集内的时频二维导频通过插值估计其子载波集内的部分信道频域响应值［33］，无需变换域处理，通过时域估计得到信道响应的全部信息。但未考虑信道在一个符号内的时变及其引起的ICI。

2008年，Karakaya B等［34］考虑了信道快速时变引起的多普勒频偏及其对LTE上行SC－FDMA系统造成的ICI影响，提出一种利用时域自适应阶数多项式进行滤波插值的快变信道估计方法;2010年，Yameogo S等［35］针对上述问题，提出利用变换域在时域通过滤波去噪的方法去除SC－FDMA系统ICI;2010年，Rabbi M F团队［36］利用基扩展模型拟合信道时域响应函数在一个符号内的时变，讨论了梳状导频辅助估计的OFDMA快变信道估计方法。上述方法属于利用导频变换到时域，跟踪信道的时域估计方法，需要导频满足频域采样定理要求的等间隔均匀分布。在实际的LTE系统及非整数倍采样信道下无法实用。

LTE频域快变信道估计的研究目前已有报道，但仅考虑了下行OFDMA。文献［37］提出了一种基于线性模型的OFDMA频域快变信道估计方法。只利用前后相邻符号用户子载波集内的梳状导频，估计频域时变传输函数各子载波在一个符号间隔内的线性时变参数，得到用户子载波集内的信道频域矩阵。文献［38］提出基于多项式基模型的LTE下行OFDMA频域快变信道估计方法，利用用户子载波集内的导频估计时变信道基系数的傅里叶变换值，从而得到用户子载波集的信道频域响应矩阵。上述OFDMA频域快变信道估计方法避免了变换到时域估计对导频的要求，不受能量泄露影响，简单实用。

4.2 研究展望

目前，针对高速移动OFDM及LTE系统中ICI问题的频域快变信道估计的研究刚刚开展，成果较少［32，36－37］，不够系统深入。在研究有效估计方法的同时，为了提高估计精度，对于信道基扩展模型的选取与优化、导频子载波本身受到ICI污染的消除及导频位置、数量的优化设计等问题都需要进一步开展系统深入的研究。

另外，现有研究均只考虑OFDM及LTE下行OFDMA系统。对于LTE上行SC－FDMA，考虑到多用户之间频偏影响，LTE建议用户数据子载波的映射采用集中式子载波分配方式［5］。为了保证单载波特性，集中子载波分配方式的导频不能插入在用户数据子载波集合内。因此，上行SC－FDMA的导频参考信号与图5所示下行OFDMA不同，为如图6所示的时分块状导频。每个资源块为时域上的、包含2个时隙的一个子帧。每个时隙有7个符号，其中第4个符号为导频参考信号，用于上行数据的解调［5］。各用户导频参考信号可频分复用，与用户占用相同的子载波集;也可码分复用，在频域导频参考信号占满所有可用子载波，通过Zad－Chu正交码分区分各用户导频［6］。针对上行SC－FDMA，如何利用其时间上相距较远、频域占用连续子载波的特殊导频模式来估计信道时变，提出有效的频域快变信道估计方法，也是值得研究与讨论的问题。

图5 LTE下行OFDMA导频参考符号图案Fig.5 Pilot pattern of LTE downlink OFDMA

图6 LTE上行SC－FDMA导频参考符号图案Fig.6 Pilot pattern of LTE uplink SC－FDMA

5 结束语

在高速移动环境下，快变信道估计与均衡是LTE系统对抗ICI、解决“双高”问题的关键，也是一项具有理论价值与实用意义的研究课题。研究表明:导频辅助估计的频域快变信道估计方法是适用于以OFDM为核心的LTE高速移动通信系统的一种实用有效的信道估计方法。LTE频域快变信道估计具体方法的研究、导频的优化设置、基扩展模型的优化选取、导频的ICI污染等问题都值得进一步开展深入的研究，相关研究必将促进宽带高速移动通信早日实现。

［1］TACHIKAWA K.A Perspective on The Evolution of Mobile Communications［J］.IEEE Communications Magazine，2003，41(10):66－73.

［2］章嘉懿，谈振辉，于晓溪，等.高速铁路公众宽带通信接入体质与关键技术综述［J］.铁道学报，2012，34(1):46－53.ZHANG Yizi，TAN Zhenhui，YU Xiaoxi，et al.Review of Public Broadband Access Systems for High－Speed Railways and Key Technologies［J］.Journal of The China Railway Socitey，2012，34(1):46－53.

［3］THEODORE S Rappaport.Wireless Communications:Principles and Practice［M］.2nd edition.Upper Saddle River，NJ:Prentice Hall，2002:124－127.

［4］MATTHIAS Pätzold.Mobile Fading Channels:Modeling，Analysis and Simulation［M］.Hoboken，NJ:John Wiley＆ Sons Ltd，2002:210－211.

［5］ETIS.3GPP TS 36.211，Physical Channels and Modulation(Release 10)V10.4.0［S］.France:3GPP Mobile Competence Centre，2011.

［6］ETIS.3GPP TR 25.814，Physical layer aspects for evolved Universal Terrestrial Radio Access(UTRA)(Release 7)［S］.France:3GPP Mobile Competence Centre，2006.

［7］RUSSELL M，STUBER G L.Interchannel Interference A－nalysis of OFDM in A Mobile Environment［C］//IEEE.45thVehicular Technology Conference.Chicago:IEEE Press，1995:820－824.

［8］MOSTOFI Y，COX D C.ICI Mitigation for Pilot－Aided OFDM Mobile Systems［J］.IEEE Transactions on Wireless Communications，2005，4(2):765－774.

［9］CAI X，GIANNAKIS G B.Low－Complexity ICI Suppression for OFDM over Time and Frequency－Selective Rayleigh Fading Channels［C］//IEEE.The Thirty－Sixth Asilomar Conference on Signals，Systems and Computers.Pacific Grove:IEEE Press，2002:1822－1826.

［10］LI Y，CIMINI L J Jr.Bounds on The Inter Channel Interference of OFDM in Time－Varying Impairments［J］.IEEE Transactions on Communications，2001，49(3):40－404.

［11］谢波，朱世华，胡刚.WCDMA系统中基于多普勒频移估计的信道估计方法［J］.通信学报，2003，24(5):140－146.XIE Bo，ZHU Shihua，HU Gang.Channel Estimation Based on Doppler Frequency Estimation for WCDMA Systems［J］.Journal of China Institute of Communications，2003，24(5):140－146.

［12］戴翔，黄登山.一种高速移动场景中的频偏校正方法［J］. 计算机仿真，2010，27(12):93－96.DAI Xiang，HUANG Dengshan.A Frequency Shift Correction Method in High Speed Vehicle Conditions［J］.Computer Simulation，2010，(12):93－96.

［13］ZHAO Y，HÄGGMAN S G.Sensitivity to Doppler Shift and Carrier Frequency Errors in OFDM Systems－The Consequences and Solutions［C］//IEEE.The46th Vehicular Technology Conference.Atlanta:IEEE Press，1996:1564－1568.

［14］ZHANG H，LI Y.Optimum Frequency－Domain Partial Response Encoding in OFDM System ［J］.IEEE Transactions on Communications，2003，51(7):1064－1068.

［15］JEON W G，CHANG K H，CHO Y S.An Equalization Technique for Orthogonal Frequency－Division Multiplexing Systems in Time－Variant Multipath Channels［J］.IEEE Transactions on Communications，1999，47(1):27－32.

［16］CHOI Yang Seok，VOLTZ P J，CASSARA F A.On Channel Estimation and Detection for Multicarrier Signals in Fast and Selective Rayleigh Fading Channels［J］.IEEE Transactions on Communications，2001，49(8):1375－1387.

［17］STAMOULIS A，DIGGAVI S N，AL Dhahir N.Intercarrier Interference in MIMO OFDM［J］.IEEE Transactions on Signal Processing，2002，50(1):2451－2464.

［18］SCHNITER P.Low－Complexity Equalization of OFDM in Doubly Selective Channels［J］.IEEE Transactions on Signal Processing，2004，52(4):1002－1011.

［19］TSATSANIS M K，GIANNAKIS G B.Modelling and E－qualization of Rapidly Fading Channels［J］.International Journal of Adaptive Control and Signal Processing，1996，10(2－3):159－176.

［20］GIANNAKIS G B，TEPEDELENLIOGLU C.Basis Expansion Models and Diversity Techniques for Blind Identification and Equalization of Time Varying Channels［J］.Proceedings of the IEEE，1998，86(10):1969－1986.

［21］HIJAZI H，ROS L.Polynomial Estimation of Time－Varying Multipath Gains with Intercarrier Interference Mitigation in OFDM Systems［J］.IEEE Transactions on Vehicu－lar Technology，2009，58(1):140－151.

［22］TEO K A D，OHNO S.Optimal MMSE Finite Parameter Model for Doubly－Selective Channels［C］//IEEE.Global Communication Conference.St Louis，USA:IEEE Press，2005:3503－3507.

［23］ZEMEN T，MECKLENBRÄUKER C F.Time－Variant Channel Estimation using Discrete Prolate Spheroidal Sequences［J］.IEEE Transactions on Signal Processing，2005，53(9):3597－3607.

［24］LEUS G.On the Estimation of Rapidly Time－varying Channels［C］//EURASIP.European Signal Processing Conference.Vienna:EURASIP，2004:227－230

［25］TANG Z，CANNIZZARO R C，LEUS G，et al.Pilot－Assisted Time－Varying Channel Estimation for OFDM Systems［J］.IEEE Transactions on Signal Processing，2007，55(5):2226－2238.

［26］代光发，陈少平.一种改进的快变信道展开模型［J］.电子学报，2010，38(7):1500－1504.DAI Guangfa，CHEN Shaoping.An Improved BEM for Fast Time－Varying Channels［J］.Acta Electronica Sinica，2010，38(7):1500－1504.

［27］张钦娟，武穆清，郭起霖，等.OFDM系统中优化的泛化复指数基扩展模型［J］.西安电子科技大学学报:自然科学版，2012，39(3):131－135.ZHANG Qinjuan，WU Muqing，GUO Qilin，et al.Optimized Generalized Complex Exponential Basis Expansion in the OFDM System［J］.Journal of xidian university，2012，39(3):131－135.

［28］Van de BEEK J J，EDFORS O，SANDELL M.On Channel Estimation in OFDM Systems［C］//IEEE.IEEE Vehicular Technology Conference.Chicago，USA:IEEE Press，1995:815－819.

［29］JIANG J，TANG T，ZHANG Y，et al.A Channel Estimation Algorithm for OFDM Based on PCC Training Symbols and Frequency Domain Windowing［C］//IEEE.International Symposium on Communications and Information Technologies.Bangkok，Thailand:IEEE Press，2006:629－632.

［30］WANG Y，LI L，ZHANG P，LIU Z.Channel Estimation for OFDM Systems inNon－Sample－SpacedMultipath Channels［J］.Electronics Letters，2009，45(1):66－68.

［31］邝育军，李云，隆克平，等.能量泄露对OFDM系统LS信道估计性能影响分析［J］.通信学报，2004，25(12):89－96.KUANG Yujun，LI Yun，LONG Keping，et al.Performance of LS Channel Estimators of OFDM Systems in Non－Sample－Spaced Multi－Fading Environment［J］.Journal of China Institute of Communications，2004，25(12):89－96.

［32］李丹，柯峰.一种基于基扩展模型的OFDM频域快时变信道估计方法［J］. 信号处理，2012，28(2):194－199.LI Dan，KE Feng.BEM Based Frequency Domain Fast Time Varying Channel Estimation Method for OFDM Systems［J］.Signal Processing，2012，28(2):194－199.

［33］李小文，潘迪.基于DSP的LTE－TDD上行信道估计实现［J］.重庆邮电大学学报:自然科学版，2010，22(1):14－18.LI Xiaowen，PAN Di.Implementation of LTE－TDD uplink channel estimation based on DSP ［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2012，28(2):194－199.

［34］KARAKAYA B，ARSLAN H.Channel Estimation for LTE Uplink in High Doppler Spread［C］//IEEE.2008 Wireless Communications and Networking Conference.Las Vegas，USA:IEEE Press，2008:1126－1130.

［35］YAMEOGO S，PALICOT J，CARIOU L.Mobile Radio Channels’Estimation for SC－FDMA Systems by Means of Adequate Noise and Inter－carrier Interference Filtering in a Transformed domain［C］//IEEE.Globecom Workshop.Miami，USA:IEEE Press，2010:1302－1306.

［36］RABBI M F，HOU S W，KO C C.High Mobility Orthogonal Frequency Division Multiple Access Channel eEtimation using Basis Expansion Model［J］.IET Communications，2010，4(3):353－367.

［37］LI D，FENG S，WU Y.Pilot－Assisted Channel Estimation Method for OFDMA Systems Over Time－Varying Channels［J］.IEEE Communications Letters，2009，13(11):826－828.

［38］EL Hajj Shehadeh Y，SEZGINER S.Fast Varying Channel Estimation in Downlink LTE Systems［C］//IEEE.21st International Symposium on Personal Indoor and Mobile Radio Communications.Paris，France:IEEE Press，2010:608－613.