利用改进的粒子群算法反演视震源时间函数

柳旭峰 许才军

（中国武汉430079武汉大学测绘学院）

引言

视震源时间函数（apparent source time function，简写为ASTF）的提取对于研究震源破裂机制和反演震源破裂过程非常重要.台站记录到的地震波形相当于格林函数、视震源时间函数（对于点源地震可视为震源时间函数）与仪器响应三者的褶积，通过反褶积过程，可以得到视震源时间函数（张勇，2008；许力生，陈运泰，2002）.

在实际求取视震源时间函数时，往往要限制一些条件，一般包括：非负性、因果性和持续时间有限性（Bertero et al，1997；张勇，2008）.反演视震源时间函数，可以在频率域中进行，常用的方法有水平线方法（water-level method）（Mori，Hartzell，1990）和光滑频谱方法（Radulian，Popa，1996）等.其优点是反演效率较高，缺点是反演结果误差较大，而且无法添加约束条件；也可以在时间域中进行，如采用共轭梯度法（许力生，陈运泰，2004）和Tikhonov正则化方法（Kraeva，2004）等，这些方法能够顾及约束条件，但反演结果随反演方法的不同而不同，并有可能陷入局部极值.Bertero等（1997）提出了在频率域中迭代的映射Landweber反褶积（projected landweber deconvolution，简写为PLD）方法，在迭代过程中将结果变换到时间域来添加约束条件，计算效率比较高，但缺点是当假定的持续时间与实际持续时间不符时，反演结果误差较大，需要在一个时间区间内对持续时间搜索来确定实际持续时间.张勇（2008）用遗传算法（generic algorithm，简写为GA）对视震源时间函数进行提取，得到了比PLD方法更好的结果，但是计算效率偏低.本文旨在利用改进的粒子群算法（particle swarm optimization，简写为PSO）反演视震源时间函数，以克服遗传算法效率偏低的缺点并获取较好的反演结果.

1 改进的PSO算法

PSO算法是由Kennedy和Eberhart（1995）提出的一种仿生学进化算法.在这个算法中，解空间中的每个解称之为“粒子”，每个粒子都有一个判别函数来量度到最优解的距离，同时还有一个速度决定粒子更新的方向和大小，在迭代的过程中，每个粒子都追随当前空间的最优粒子（Poli et al，2007）.

设PSO算法解空间有m个粒子，初始值为x0＝（x01，x02，…，x0m），初始速度为v0＝（v01，v02，…，v0m）.在每次迭代中，每个粒子通过跟踪两个极值来更新自己，第一个极值为粒子本身在迭代过程中的最优解，称为个体极值（pbest）；另一个极值是整个种群当前的最优解，称为全局极值（gbest）.设在第n次迭代后，解空间为xn＝（xn1，xn2，…，xnm），对应的速度为vn＝（vn1，vn2，…，vnm），则第n＋1次解空间xn＋1可以表达为

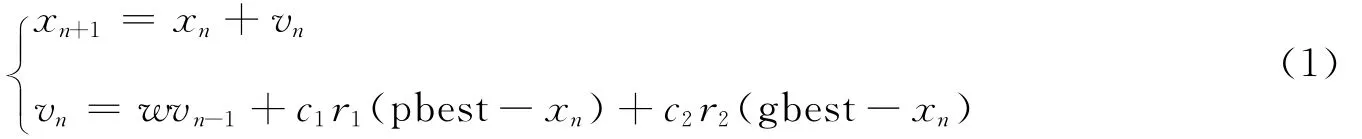
式中，w为惯性因子，表示前一时刻粒子速度对当前时刻粒子速度的影响，取值范围为［0，1］；c1是粒子自身速度学习因子，表示粒子向自身最优值学习；c2是群体速度学习因子，表示粒子向群体最优值学习；r1和r2为0与1之间的随机值，是调节粒子向自身学习和群体学习的权重系数.每次迭代中，计算每个个体的判别函数值F，并更新个体极值和全局极值.判别函数值F是当前解与最优解之间差值的量度，一般在［0，1］之间，当F为0时，表示达到最优解.同时为了限制PSO算法的更新速度过大或者过小，往往根据经验或者试算结果假定粒子最大速度vmax和最小速度vmin，超过则取最大值，不足则取最小值.在迭代过程中，还可以随机对空间中的粒子的速度进行变异操作，以达到全局优化的目的.

PSO算法虽然属于全局优化算法，但在迭代过程中，所有解都趋向于最优解进行更新，有可能陷入局部解.另外，相对于遗传算法，PSO算法中引入速度概念，加快了算法的收敛过程.但如果惯性因子不变，则算法在后期容易来回震荡，导致效率降低.

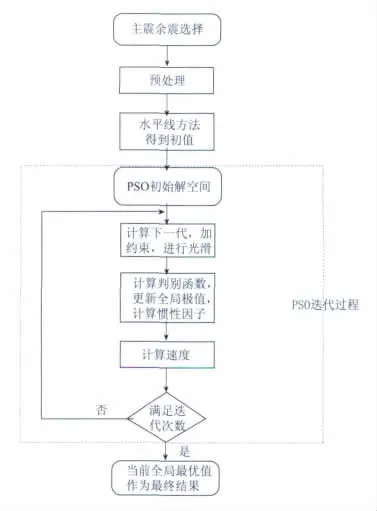
图1 改进的PSO算法流程图Fig.1 Flow-chart of the improved PSO algorithm

考虑到PSO算法存在的问题，本文对PSO算法进行了改进（改进方法的流程如图1所示）.具体内容包括以下4点：

1）初值的选取.为了提高PSO算法的收敛速度，并且克服陷入局部解的倾向，本文利用水平线方法得到的初值添加约束之后的结果作为PSO算法初始全局最优解.水平线方法原理如下：

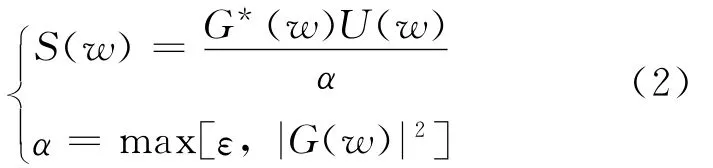
式中，ε称为阈值因子；max［ε，｜G（w）｜2］表示取ε和｜G（w）｜2的较大值.得到的S（w）经过反傅里叶变换，可以得到在时间域中表示的视震源时间函数.根据非负性和持续时间有限性约束，令结果中负值为0，并且在假定持续时间之外的值为0，将得到的结果作为PSO算法的初始全局最优解.在初始全局最优解周围一定范围内随机产生m个解，形成PSO算法的初始解空间.

2）判别函数的选择.判别函数表示得到的结果与真实结果的距离大小的量度.本文中采用直观的方式.

设U（t）表示真实主震记录，Usyn（t）表示通过解空间中的解得到的合成记录.定义数据误差Vd为

式中，t表示持续时间.令F＝Vd表示判别函数.

3）对惯性因子的改进.为了使算法迭代后期不至于在最优值附近来回震荡，要求惯性因子在判别函数变小时减小，因此设计

式中，c0和c1为常数；F（n）min表示第n次迭代解空间判别函数的最小值；F（n）i表示第n次迭代解空间中第i个解的判别函数值；后面的指数函数随着迭代次数n的增大而减小.c1的数值不能取太大或者太小.太大会使得这个函数没有意义，起不到相应的减小速度的效果；太小则会使迭代速度减小过于迅速，算法的效率下降.实际计算中，c0和c1的值根据经验取得.

4）为了提高收敛速度，去掉了PSO算法的自身学习成分，即令PSO算法的自身学习权重c1＝0.

改进的PSO算法的迭代公式为

2 利用改进的PSO算法反演模拟视震源时间函数

采用一个包含两个峰值的模拟视震源时间函数作为真值，一个经过低通滤波的地震波信号作为经验格林函数（empirical Green’s function，简写为EGF），合成模拟主震记录.同时，对合成的主震记录添加噪声，在不同的噪声水平下，采用改进的PSO算法、PLD方法以及GA算法分别对视震源时间函数进行反演，对比说明改进方法的优缺点.

在合成的模拟主震记录中加入噪声，关系式为

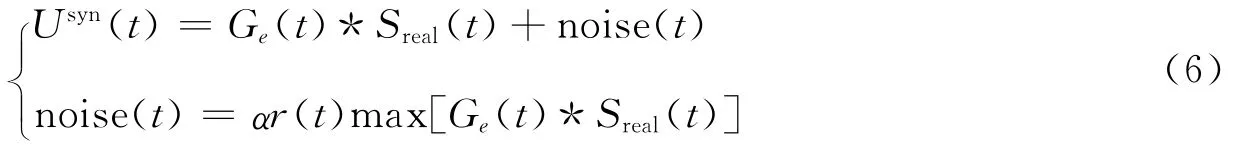
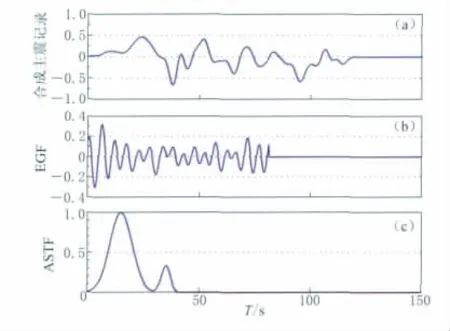
图2 合成主震记录（a）、0.25Hz滤波后的EGF（b）和模拟 ASTF（c）图Fig.2 Synthetic main shock record（a），empirical Green function（EGF）filtered by 0.25Hz low pass（b）and simulated ASTF（c）

式中，＊表示卷积；α为噪声水平；r（t）为［0，1］上均值为0、方差为1的高斯白噪声序列；max［Ge（t）＊Sreal（t）］表示取模拟主震记录振幅的最大值.

模拟视震源时间函数总共持续时间40s，包含两段过程，每段采用高斯函数生成.经验格林函数采用GNI台站观测到的2005年克什米尔MW7.6地震的一次余震记录的P波数据，经过8阶Butterworth低通滤波器进行滤波，滤波上限为0.25Hz，通过与模拟的视震源时间函数褶积得到模拟的主震记录（图2）.

定义模型误差Vm为

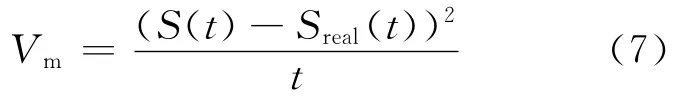
式中，S（t）为反演得到的视震源时间函数，t为持续时间.

采用0，0.1和0.3的噪声水平，当模型误差Vm＝0.001时终止迭代.假定最大迭代次数为2 000（试验表明，PLD方法迭代2 000次之后模型误差基本不变），并且假定视震源时间函数持续时间长度为100s，反演结果如图3—5所示.

反演资料时间间隔为0.25s，反演过程中水平线方法的阈值因子采用0.3，三种方法的初始值都选择了水平线方法得到的结果并加入了约束条件.在迭代过程中构造拉普拉斯方程进行时间光滑.令▽2s（t）＝0，即s（t－1）＋s（t＋1）－2s（t）＝0.PLD方法的松弛因子选择为1／｜Gmax（w）｜2；PSO算法种群个数为200，式（4）中c0取值为2，式（5）中c2取值为2；GA算法中种群个数为200，种群变异因子为0.4，交叉因子为0.5，选择因子为0.1，在计算过程中采用了退化方法：设第i次迭代的结果为Si（t），m为Si（t）的中位数，那么第i次迭代的实际结果为si（t）－mi.

从图3—5反演的结果可以看出，改进的PSO算法与GA算法结果相似，但都好于PLD方法.在持续时间（40s）之外，随着噪声的增大，PLD方法的误差变大，而改进的PSO方法和GA算法误差都比PLD方法误差小.

从模型误差可以看出，改进的PSO算法能够用较少的迭代次数得到较优结果.PLD方法得到的模型误差在一定的迭代次数之后趋于稳定，反演结果无法继续收敛，表现为最大幅值一直处于0.9以下.而且PLD方法在各种噪声水平下都无法收敛到终止迭代误差（即模型误差为0.001）.其原因在于，由于添加了拉普拉斯平滑，使得PLD迭代结果失真，从而导致最终结果失真，而对不添加拉普拉斯平滑的PLD方法进行的试验结果表明，噪声存在情况下，PLD方法的反演结果不平滑，模型误差较大.在0.3噪声水平下，3种方法都无法收敛.从图5可以看出，改进的PSO算法得到的结果与实际视震源时间函数最为吻合.同样迭代2 000次，改进的PSO算法的计算时间比GA算法要少一倍，而且PSO算法在迭代200次左右模型误差就不发生变化.考虑到这一点，在0.3噪声水平下3种方法所用时间比例与低噪声水平时基本不变.本研究中多次计算统计表明，改进的PSO算法相比GA算法计算时间减少了80%以上，效率提高了至少5倍.

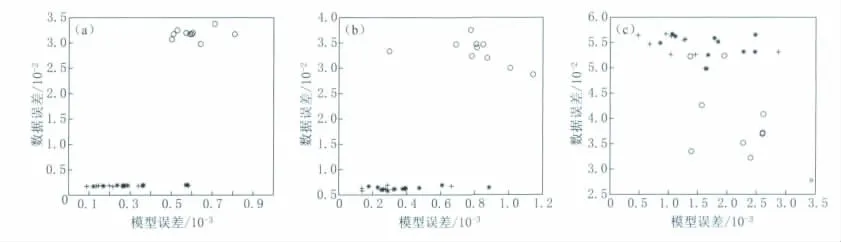
图6 不同噪声水平下改进的PSO算法、PLD方法和GA算法计算得到的模型误差与数据误差（a），（b），（c）分别对应0.05，0.1和0.3的噪声水平.圆圈表示PLD方法所得结果，星号为改进的PSO算法所得结果，十字为GA算法所得结果Fig.6 Model errors and data errors inversed from improved PSO，PLD and GA under different noise levels（a），（b）and（c）correspond to noise levels 0.05，0.1and 0.3，respectively.Circles，stars and crosses stand for inversion results from PLD，the improved PSO and GA，respectively

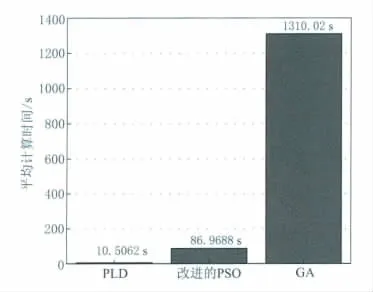
图7 PLD、改进的PSO和GA三种方法的平均运行时间Fig.7 Average computing time for using PLD，the improved PSO and GA

为了进一步说明改进的PSO算法、GA算法以及PLD方法在反演结果上的优劣，分别在0.05，0.1和0.3噪声水平下采用3种方法进行了计算.改进的PSO算法粒子个数为200，迭代次数200；PLD方法迭代次数为2 000；GA算法种群个数采用1 000，迭代次数500，其它参数不变.以模型误差和数据误差作为指标，此时3种方法得到的反演结果基本不变（图6）.计算图6所需的3种方法的平均时间如图7所示.

从图6和图7可以看到，采用改进的PSO算法和GA算法得到的结果相对于PLD方法更为稳定，表现为分布更为集中.改进的PSO算法在种群个数和迭代次数均较少的情况下能够得到与GA算法相当的效果.可见改进的PSO算法一方面能够克服GA算法效率低的特点，另外还能够得到相比PLD方法更为准确的结果.

3 2005年巴基斯坦克什米尔MW7.6地震P波视震源时间函数反演

2005年10月8日巴基斯坦克什米尔地区发生了MW7.6地震.该地震位于印度板块与欧亚板块碰撞带上喜马拉雅山地震带西部.此处印度板块向北运动，与欧亚板块发生碰撞，印度洋板块向下俯冲，引发地震.继主震发生之后，又发生了多次余震（表1）.因此，我们可以利用经验格林函数的方法提取视震源时间函数.

表1 2005年克什米尔MW7.6地震主震及余震序列Table 1 Information on the 2005Kashmir MW7.6main shock and its aftershocks

张勇（2008）采用GA算法和PLD方法，利用31个台站观测到的主震和余震数据对视震源时间函数进行了反演.结果表明，此次地震的视震源时间函数持续时间在25s以内，P波视震源时间函数相比S波的要短.

张勇等（2009）利用PLD方法对此次地震的P波、S波、瑞雷波和勒夫波视震源时间函数进行了提取.结果表明，此次地震的视震源时间函数平均持续时间为25s，不同震相的结果形状大致相似，细节略有不同.

本文利用改进的PSO算法对此次地震的P波视震源时间函数进行提取.从美国地震学联合研究会（IRIS）数据中心下载了64个台站记录的克什米尔地震的主震及11次余震的Z分量数据，并选择信噪比大于4的台站数据.通过去趋势项、去平均项，并进行降采样处理，使资料采样间隔统一变为0.5s.采用8阶Butterworth滤波器进行低通滤波，滤波上限为0.25Hz.参考P波理论到时，截取P波初到时与S波初到时之间的数据.假设视震源时间函数持续时间为50s，利用经验格林函数的方法，对P波视震源时间函数进行提取，并且对每个台站得到的多个视震源时间函数归一化后进行叠加.剔除掉反演较差的结果，总共得到40个台站的P波视震源时间函数，如图8、图9所示.

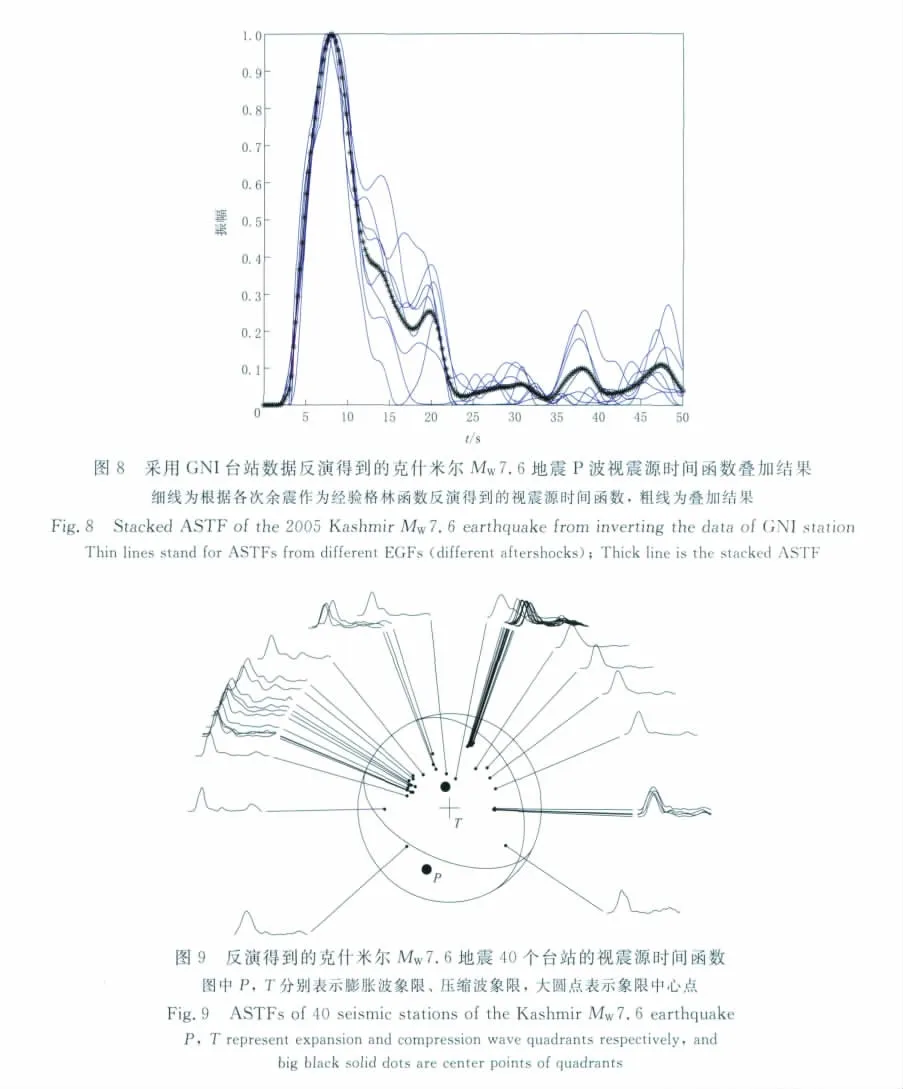
通过对台站的视震源时间函数进行对比可以看出，得到的P波视震源时间函数持续时间在25s以内，各个台站得到的视震源时间函数相似，说明利用改进的PSO方法能够有效地提取视震源时间函数.对各个不同方位角的台站的视震源时间函数的对比显示，位于震中西北方向的视震源时间函数相对于东南方向较快地出现峰值，由此可见，震源的破裂方向应该是西北向的.这些结果与张勇（2008）和张勇等（2009）的结果一致.

研究中还发现，台站资料的信噪比对于提取视震源时间函数非常重要，台站记录到的信噪比越高越好.

4 讨论与结论

视震源时间函数的提取对于研究震源破裂过程十分重要.传统的频率域反演方法，如水平线方法，往往无法加入约束；而传统的时间域方法，如共轭梯度法，则反演效率低，并且易于陷入局部极值.本文研究表明，PLD方法同时顾及约束和效率，得到的结果好于传统方法.而GA算法能够得到比PLD更好的结果，但GA算法计算效率相对较低.考虑到PSO算法在GA算法基础上引入了速度的概念，能够极大提高计算效率.因此本文提出利用改进的PSO算法对视震源时间函数进行反演研究.

利用模拟数据，对改进的PSO算法、GA算法和PLD方法的计算效率和计算结果的准确性进行了对比.结果表明，改进的PSO算法比GA的计算效率提高了5倍以上，而相比于PLD算法，改进的PSO算法计算所得结果的准确性则有很大提高.说明了改进的PSO算法能够有效地反演视震源时间函数.

利用改进的PSO算法对2005年巴基斯坦克什米尔MW7.6地震的P波视震源时间函数进行了提取，得到了40个台站的视震源时间函数.结果表明，此次地震的P波视震源时间函数持续时间在25s以内，破裂方向为西北方向.该结果与张勇（2008）和张勇等（2009）的结果一致.

此外需要指出的是，台站数据质量对于提取视震源时间函数也是非常重要的.

许力生，陈运泰.2002.震源时间函数与震源破裂过程［J］.地震地磁观测与研究，23（6）：1－－7.

许力生，陈运泰.2004.从全球长周期波形资料反演2001年11月14日昆仑山口地震时空破裂过程［J］.中国科学：D辑，34（3）：256－－264.

张勇.2008.震源破裂过程反演方法研究［D］.北京：北京大学地球物理学系：1－－70.

张勇，许力生，陈运泰.2009.提取视震源时间函数的PLD方法及其对2005年克什米尔MW7.6地震的应用［J］.地球物理学报，52（3）：672－－680.

Bertero M，Bindi D，Boccacci P，Cattaneo M，Eva C，Lanza V.1997.Application of the projected Landweber method to the estimation of the source time function in seismology［J］.Inverse Probl，13（2）：465－－486.

Kennedy J，Eberhart R.1995.Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks，4：1942－－1948.

Kraeva N.2004.Tikhonov’s regularization for deconvolution in the empirical Green function method and vertical directivity effect［J］.Tectonophysics，383（1）：29－－44.

Mori J，Hartzell S H.1990.Source pulse enhancement by deconvolution of an empirical Green’s function［J］.Geophys Res Lett，12（1）：33－－36.

Poli R，Kennedy J，Blackwell T.2007.Particle swarm optimization［J］.Swarm Intell，1（1）：33－－57.

Radulian M，Popa M.1996.Scaling of source parameters for Vrancea（Romania）intermediate depth earthquake［J］.Tectonophysics，261（1）：67－－81.