渗流系统灰色数值模型输出结果的灰度分析
李树文,张大龙,李 尧
(1.河北工程大学,河北 邯郸056038;2.河北工业大学,天津300401)
邓聚龙教授建立的灰色朦胧集理论,很好的解释了“经典”思维方法的不足,填补了数学模拟中“连续”与“离散”的鸿沟,是灰数学(灰理论)的基础[1,2]。对于地下水流系统基本灰色数值模型的解算,须以朦胧集为前提,保证灰信息传递的正确性,因为泛灰数[3]、区间型灰数[4]及其运算性质以及区间型灰色线性方程组的解法,都是以朦胧集为出发点的。文献[5]和文献[6]建立了基于灰色数学基础的渗流问题的灰色有限元数值模型,本文在其基础上,分析渗流系统输入信息的灰度对输出信息灰度的影响。在给出渗流系统灰色数值模型的基础上,通过一个算例,分析当模型的输入信息(包括导水系数、储水系数、入渗水量)取不同的灰度时,模型的输出结果——水位灰度将出现如何的变化。这个讨论,对于模型的实际应用具有特殊的意义。
1 渗流问题的灰色数值模型
把渗流问题中的参数和变量视为灰参数和灰变量,根据质量守衡和能量守衡定律,可以得到渗流问题的灰色微分方程[7]:
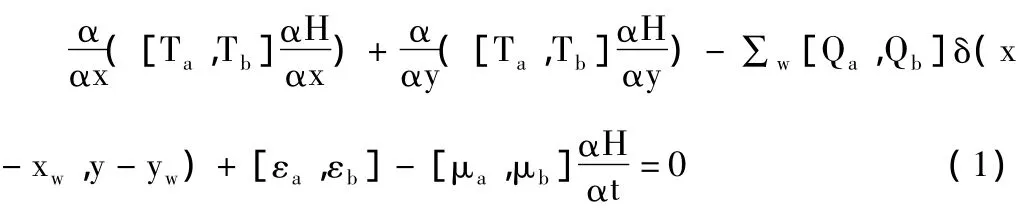
对以上方程运用伽辽金(Galerkin)有限元方法进行离散,可得任一结点i的灰色有限元方程:

Ta,Tb表示灰色导水系数的上界和下界;Ha,Hb表示灰水位的上界和下界;Qa,Qb表示开采量的上界和下界;εa,εb表示灰色入渗补给量的上界和下界;μa,μb表示灰色储水系数的上界和下界;qa,qb表示灰色边界补给量的上界和下界。
为了叙述问题简便,将方程(2)简记为:

基于有理灰数运算规则[4],可以将方程(2)逐项计算[5,6]。对于 Ⅰ1项计算,要特别注意其中的 αi,αj,αk的符号问题,αi总是大于零的,而αj,αk符号有正有负,因此应据不同情况讨论,即:
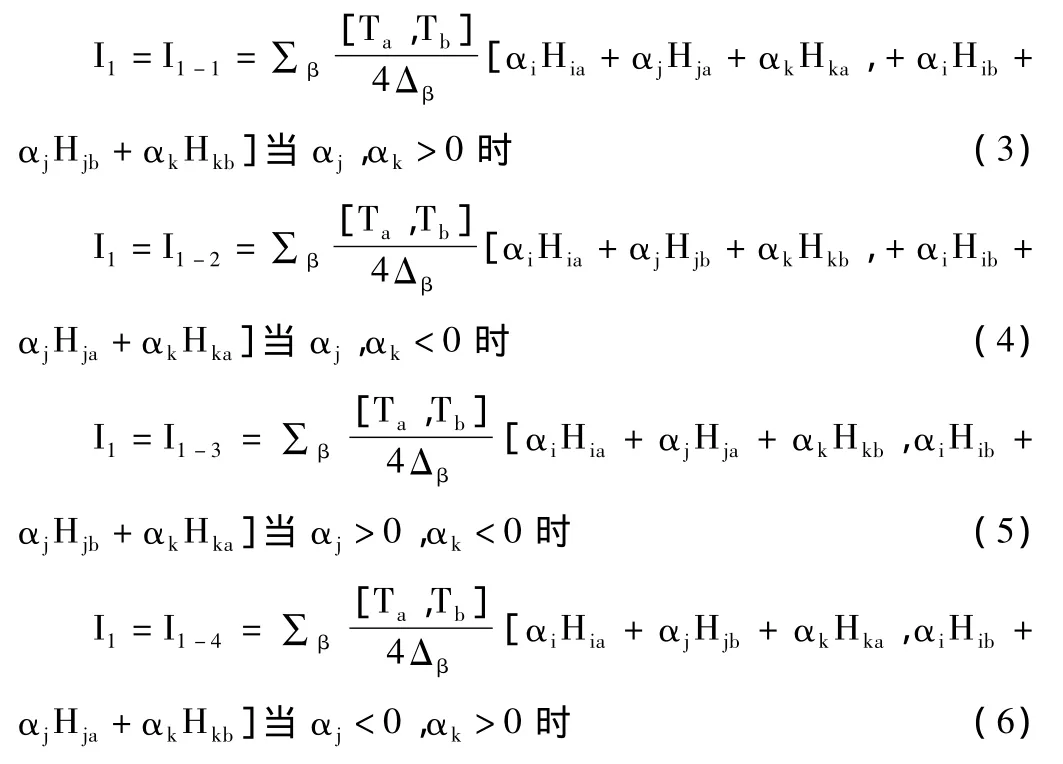
其它各项分别为:
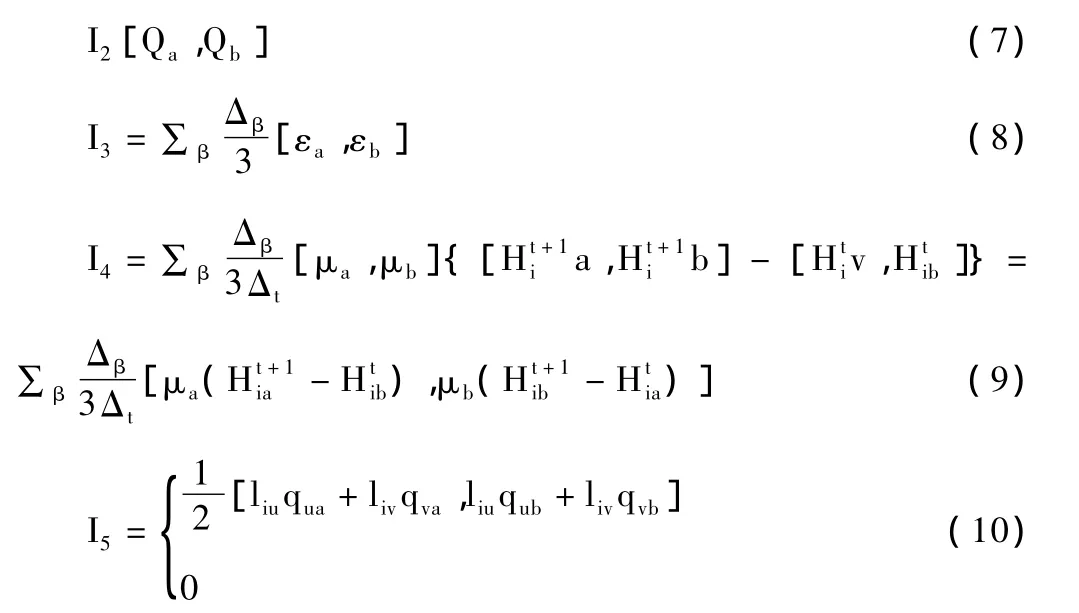
将式(3)至(10)代入方程(2)中,得到四种情况下结点i的灰色有限元方程。
第一种情况:当 αj,αk>0 时
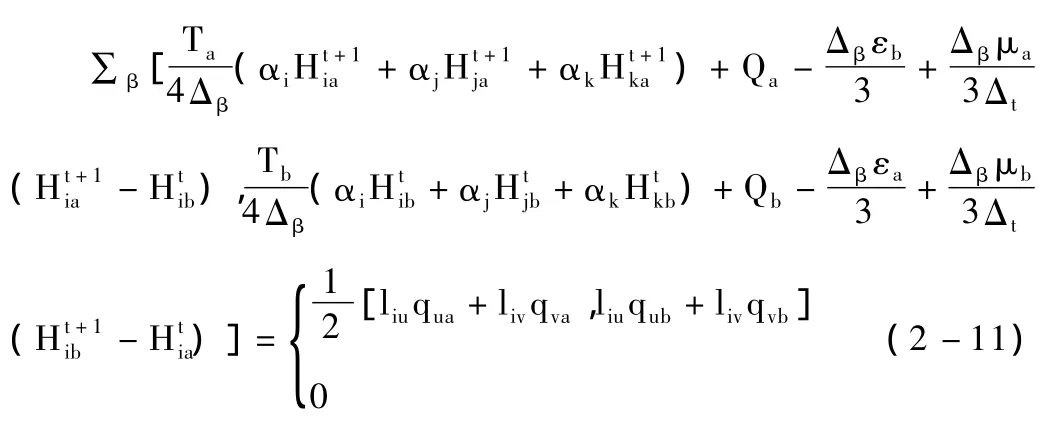
依次可以写出 αj,αk<0,αj>0,αk<0 和 αj<0,αk>0其它三种情况下的结点灰色有限元方程[5,6](略)。
2 模型计算结果的灰度分析
以上所述的灰色数学模型,描述的是渗流系统的灰水位的时空变化。模型实际应用中,其输出结果——灰水位的灰度能否在一个较小的、实用的范围内变化,是十分重要的。根据灰色系统理论,灰数是确知量和未知量的总体。而灰度是灰数未知程度的量度,或者说灰数的未知程度称为灰数的灰度。下面用一个算例,来分析实际应用中普遍关心的问题,即灰色输入量的灰度对灰色输出量水位灰度的影响问题。
一个符合泰斯条件[7]的承压含水层。含水层被剖分成30个三角形单元,23个结点,其中内结点9个。6号、8号为抽水井的结点。计算时段划分为3个,即0.3日,0.2日,0.5日。初始水位标高取为100 m,计算区域的边界由泰斯解析解公式计算后给出,即全为第一类边界条件(图1)。
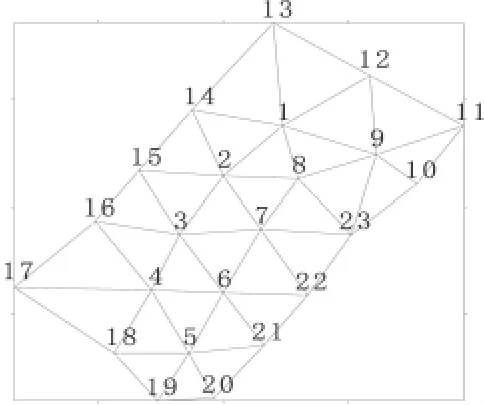
图1 计算区剖分图
2.1 导水系数灰度对水位灰度的影响
为了说明这个问题,将导水系数分别取作9个区间灰数[Tia,Tib](i=0,1,…,8),然后求得 7 号结点第三个时段末的相应的9个灰色水位结果(表1)。并根据计算结果绘制了导水系数灰度对水位灰度影响的关系曲线分别为初值化的水位增量和初值化的导水系数增量,这是一种数据变换方法。这样的做法大大加强了水位值和导水系数的可比性,便于数据和图形的对比分析。
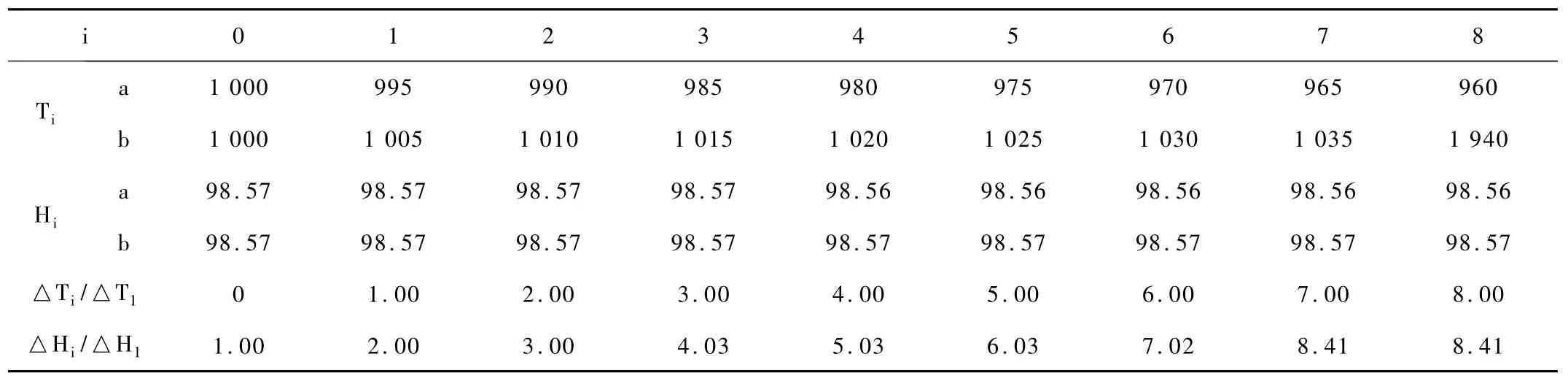
表1 导水系数灰度对水位灰度的影响结果

图2 导水系数灰度对水位灰度影响关系曲线
采用同样的方法,可获得垂向入渗量灰度对水位灰度的影响关系曲线(图3)。

图3 灰色输入量灰度对水位灰度影响关系曲线
从图3可以看出,随着灰色导水系数灰度、灰色垂向入渗量灰度的增加,水位灰度受其影响,呈直线上升且直线的斜率近 45°。
2.2 储水系数灰度对水位灰度的影响
储水系数灰度对水位灰度的影响,其分析方法与上述方法相同。两者灰度的影响关系见图4。从图4中可以看出,随着储水系数灰度变化,水位灰度不成线性变化。对于不同的计算时段,其变化关系也不相同。第一时段的关系曲线基本上呈直线上升,直线的斜率稍大于45°,并且在曲线的上端上升幅度小,即有所收敛;第二计算时段和第三计算时段,两者的关系呈曲线跳跃,且跳跃的最大值是有限的。
3 结语
(1)灰色数值模型中的运算并不等于简单的区间计算,而它的理论基础是朦胧集、灰数运算性质。
(2)灰色输入量的灰度对灰色输出量灰度的影响是:水位灰度随着导水系数灰度(或入渗水量的灰度)增大呈线性增大的变化,其变化的斜率呈45°;随着储水系数灰度变化,水位灰度不呈线性变化,两者的关系呈曲线跳跃,且跳跃的最大值是有限的。
(3)模型实际应用中,减小水位灰度的办法是合理把握输入信息的灰度,做到这一点并不困难。

图4 储水系数灰度对水位灰度影响关系曲线
[1]邓聚龙.灰数学引论-灰朦胧集.武汉华中理工大学出版社.1992.9.
[2]邓聚龙.灰理论基础.武汉华中科技大学出版社.2002.
[3]王清印等.泛灰集与点灰数.灰色系统理论与实践.济南:1991;(1).
[4]王清印.灰色数学基础.武汉华中理工大学出版社.1996.9.
[5]Wu Qing,Li Shuwen,Wang Yinao,Dong Donglin.A research on grey numerical imitation and modeling of groundwater seepage system.China Science(D),Vol.44 No.11,2001:1043-1056.
[6]李树文,王义闹,赵秀娟.渗流问题灰色数值模型的解法研究.数学的实践与认识.2004,34(3).
[7]陈崇希,林敏.地下水动力学.武汉中国地质大学出版社.1999.

