基于遗传算法的Bézier曲线降多阶逼近
温州大学物理与电子信息工程学院 于世亮
温州医学院生物信息工程学院 白宝刚
1.引言
参数曲线曲面在许多造型系统中都有重要的应用,不同的造型系统中多项式基的次数是不同的,如果在系统间进行数据传递[1],就需要将参数曲线曲面的阶数统一起来。由于高阶曲线可以精确的表示低阶曲线,一般来讲,低阶曲线却不能精确表示高阶曲线,近年来,参数曲线曲面的降阶问题引起了国内外许多学者的兴趣。同时,降阶曲线可以减少数据的存储量,提高了造型系统的效率。此外,降阶处理也应用在曲线的光顺处理过程中[2]。
Bézier曲线由于本身具有的良好的性质,被广泛应用于计算机辅助设计和制造,国内外许多学者研究了Bézier曲线的降阶问题[3-6]。Hoschek[3]首先对原曲线进行离散,然后利用原曲线的几何信息,通过多段低阶曲线来插值逼近原曲线;Worsey[4],Lachance[5]及Eck[6]利用Chebyshev多项式理论,对降阶进行了研究;胡事民[7]提出了B网扰动和约束优化的方法等。这些方法只进行了一次降阶,如需多次降阶,则要循环运用算法,这样一方面是计算繁琐耗时大,另一方面是误差有可能会很大。2002年陈国栋和王国瑾[8]给出了带端点插值条件的Bézier曲线一次降多阶逼近方法;郑建民和汪国昭[9]着眼于几何逼近技术,对原曲线控制顶点作最小扰动来得到约束降多阶曲线。这些研究或者计算繁琐,或者没有很好的误差估计,逼近精度未必最佳,或者没有降阶后曲线的显式表示。本文在上述研究的基础上,应用遗传算法的性质特点,与Bézier曲线降阶相结合,运用matlab工具箱实现了多次降阶。
2.问题描述
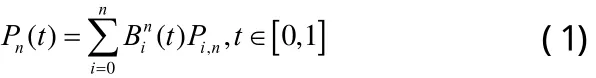
所谓n次Bézier曲线Pn( t)降多阶到m次,即寻找另一组控制顶点所确定的m次Bézier曲线,使得降阶前后两条曲线之间的距离函数:
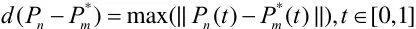
达到最小。本文只讨论n次Bézier曲线降阶的非退化情形,上述问题可转化为如下的带端点约束的最优化问题:
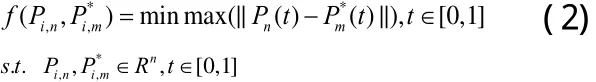
传统的解决最优化问题存在各种弊端,而遗传算法(Genetic Algorithm,简称GA)是以自然选择和遗传理论为基础,将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法,与传统的搜索方式相比较,具有如下优点:
a.遗传算法的操作对象是一组可行解,而非单个可行解;搜索轨道有多条,而非单条,因而具有良好的并行性。
b.遗传算法只需要利用目标的取值信息,而无需梯度等高价值信息,因而适用于任何大规模、高度非线性的不连续多峰函数的优化以及无解析表达式的目标函数的优化,具有很强的通用性。
c.遗传算法择优机制是一种软选择,加上其良好的并行性,使它具有良好的全局优化和稳健性。
d.遗传算法操作的可行解是经过编码化的(通常采用二进制编码),目标函数解释为编码化个体(可行解)的适应值,因而具有良好的可操作性和简单性。
3.算法描述
3.1 编码方法
我们采用实数编码,直接使用问题变量进行编码,避免了二进制编码对解的精度限制,提高了遗传算法的精度要求;无需编码解码,改善了遗传算法的计算复杂性,提高了运算效率。我们将每次产生的m个控制点组成解向量,成为一个个体。
3.2 初始群体的生成
产生随机数αi∈[0,1],i=0,...,m,然后应用
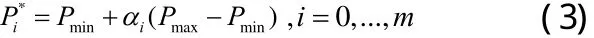
求出降阶后的控制顶点,即一个个体,然后根据群体大小,得到初始群体。Pmin和Pmax为Bézier曲线左右降一阶然后分别递归执行n- m-1次所得到的控制点,为保证端点的插值性,令
3.3 适应值函数
适应值函数即个体评价函数,函数值越大表示适应能力越好,符合适者生存的生物进化规律,一般而言,适应值函数的设定需要从目标函数转换得来,我们采用的是实数编码,适应值函数取:
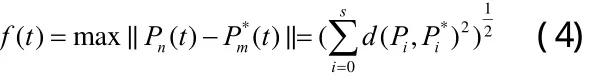
其中, Pi和是降阶前后曲线上的点。
3.4 遗传算子
选择:轮盘赌选择由于使个体实际被选中的次数与它应该被选中的期望值之间可能存在着一定的误差,因此这种选择方法的选择误差比较大,有时甚至连适应度高的个体也选不上。我们采用随机竞争选择方法,每次按轮盘赌选取一对个体,然后让这两个个体进行竞争,适应度高的被选中,反复进行,直到选满。
交叉:群体中的个体采取随机配对的策略,交叉操作是在这些配对个体组中两个个体之间进行,双亲的染色体以杂交的方式产生出子代染色体,从而使子代染色体继承了双亲的遗传特性,为了保证杂交产生的后代,其分量仍在[Pmin,Pmax]上,同时相应于实数编码,我们采用非均匀算数杂交,假设两个父解向量为:
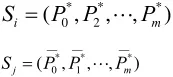
经杂交产生两个后代为:
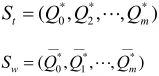
则他们之间有如下关系:
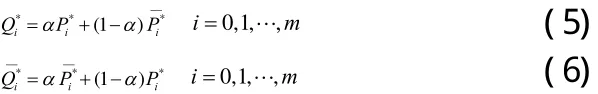
其中α∈[0,1],为随机数。
变异:变异运算虽然只是产生新个体的辅助方法,但它也是必不可少的一个步骤,它决定了遗传算法的局部搜索能力,此外,变异运算维持了群体的多样性,防止出现早熟现象。采用均匀变异的方法,依次指定个体编码串中的每一个基因座为变异点,对每一个变异点以设定的变异概率从对应基因的取值范围内取一随机数来代替原有值。
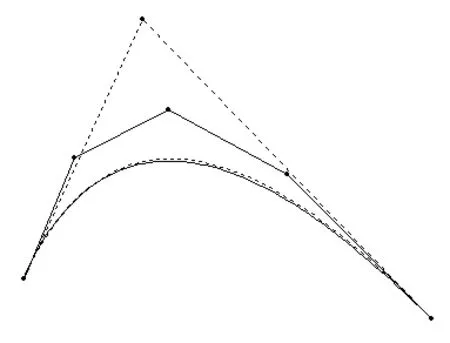
图1 四次Bézier曲线降到两次Bézier曲线

图2 五次Bézier曲线降到三次Bézier曲线
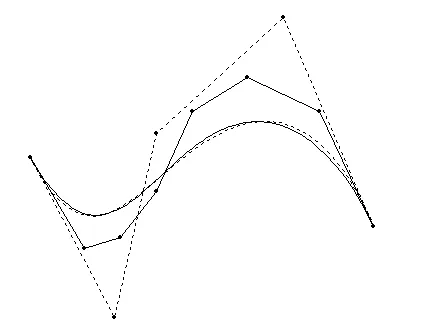
图3 七次Bézier曲线降到四次Bézier曲线
3.5 控制参数
遗传算法中,控制参数的选择非常关键,参数包括群体的规模N、交叉概率cP、变异概率Pm、进化代数T等。太大的交叉概率可能是搜索走向随机化,太小则进化速度变慢;变异概率适当增大可维持群体的多样性,搜索过程可跳出局部,收敛到全局最优。本文在分别在以下参数范围做了大量实验:150-200,200-250,0.4-0.99,0.0001-0.1。
3.6 实现步骤
Step1.输入降阶前的控制顶点 Pi,i=0,1,···,n-1,输入需要降阶到的m值。
Step2.求左右降一阶的控制点顶点并递归n-m-1次,求得最终的m对控制顶点。
Step3.绘制降阶前的控制顶点和曲线。
Step4.初始化初始化群体代数和控制参数及误差。
Step5.产生初始群体。
Step6.计算群体的每个个体的适应值.
Step7.若迭代次数小于群体代数或每个个体的适应值大于给定误差,转Step8;否则,转Step9。
Step 8.进行选择杂交产生新的子代,返回Ste p 6。
Step 9.绘制降阶后的Bézier曲线的控制多边形及曲线。
4.误差分析
n次Bézier曲线P( t)降n-m次得到m次Bézier曲线,将降阶后的曲线升n-m-1次,得到n-1次Bézier曲线x( t),与原曲线的误差为:

5.数值实验
例1:降两阶,给定五个控制点:
{90,150},{150,300},{260,360},{400,280},{570,100}的四次Bézier曲线,降两阶得两次Bézier曲线,产生三个控制点为:{90.0000,150.0000},{229.8573,472.2235},{570.0000,100.0000},如图1,其中虚线代表降阶后的控制多边形和曲线,实线代表降阶前的控制多边形和曲线(下同),误差为:3.012745。
例2:降两阶,给定六个控制点:
{70,280},{150,450},{250,410},{360,300},{450,260},{600,420}的五次Bézier曲线,降两阶后,得到由四个控制点:{70.0000,280.0000},{203.7269,571.3842},{396.4577,150.1183},{600.0000,420.0000}控制的三次Bézier曲线,如图2,降阶前后曲线误差为:5.198758。
例3:降三阶,给定八个控制点:
{10,80},{25,40},{35,45},{45,65},{55,100},{70,115},{90,100},{105,50}所确定的七次Bézier曲线,降三阶,得到五个控制点为:{10.0000,80.0000},{33.2864,9.7327},{45.0332,90.4035},{79.9754,141.6573},{105.0000,50.0000},产生降阶后的四次Bézier曲线,如图3,误差为:6.342841。
6.结论
基于遗传算法,根据Bézier曲线的基本性质,实现了Bézier曲线保端点的多次降阶,实验表明,降阶效果好,直观性强。
[1]DANNEBERG,L,NOWACKI,H.Approximate conversion of surface representations with polynomial bases[J].Computer-Aided Geometric Design,1985,2(2):123-132.
[2]FARIN,G.Degree reduction fairing of cubic B-Spline curves[J].In:Barnhill,R,E,ed.Geometry Processing for Desiging and Manufactur-ing.Philadelphia:SIAM,1992.87-99.
[3]HOSCHEK,J.Approximation of spline curves[J].Computer-Aided Geometric Design,1987,4(1):59-66.
[4]WATKINS,M,WORSEY,A.Degree reduction for Bézier curves[J].Computer-Aided Design,1988,20(7):398-405.
[5]LACHANCE,M A.Chebyshev economization for parametric surfaces[J].Computer-Aided Geometric Design,1988,5(3):195-208.
[6]ECK,M,A.Degree reduction of Bézier curves[J].Computer-Geometric Design,1993,10(4):237-257.
[7]HU SM,SUN JG,JIN TG,WANG GZ.Approximate degree reduction of Bézier curves[J].Tsinghua Science and Technology,1998,3(2):997-1000.
[8]GUO-DONG CHEN,GUO-JIN WANG.Optimal multi-degree reduction of Bézier curves with constrains of endpoints continuity[J].Computer Aided Geometric Design 19(2002):365-377.
[9]Zheng J M,Wang G-Z,Perturbing Bézier coefficients for best constrained degree reduction[J].Graphical Models,2003,65(6):351-368.

