基于MATLAB的反鱼雷鱼雷固定提前角导引弹道仿真*

潘 光，杨 悝

(西北工业大学航海学院，西安710072)

0 引言

随着鱼雷技术的发展和性能的不断提高，鱼雷成为众矢之的，反鱼雷成为海战中的一项重要任务[1]。世界发达国家在提高探测设备性能的同时，开始研发反鱼雷鱼雷，它是近年来发展起来的一种反鱼雷武器，它与其它软对抗手段一起，构成较为完善的防御系统以提高舰艇的生存能力。

与其它反鱼雷器材相比，反鱼雷鱼雷具有主动对抗性，拦截范围大，机动性强等优点[2]。其主要难点有:拦截时间窗口小，探测来袭鱼雷难度大等问题。根据以上特点，反鱼雷鱼雷必须具备灵敏、快速的自导系统以及机动性优良的控制系统。

文中在鱼雷攻击舰艇的典型工况下，采用Matlab/Simulink完成了基于固定提前角导引法的反鱼雷鱼雷拦截来袭鱼雷的弹道设计与仿真，同时分析比较了不同的运动参数下对其弹道特性的影响。

1 固定提前角导引法

固定提前角导引法是现代鱼雷声自导中较常见的一种方法[3－5]。固定提前角导引要求在自导导引过程中，鱼雷自导装置能测出目标相对于鱼雷的运动方向及视线相对提前角的偏差，并根据偏差产生自导操纵指令送到控制系统，由控制系统按指令操舵使鱼雷的速度方向以固定提前角指向目标运动的前方。其相对运动方程组为:

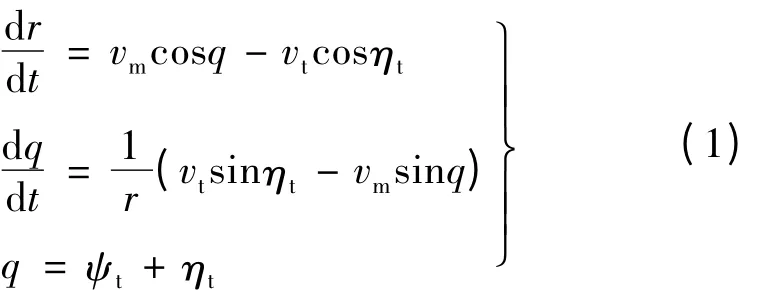
此外，还有约束方程:

式中:t表示鱼雷的位置;m表示目标的位置;r表示鱼雷与目标之间的距离;q表示视线与攻击平面内某一基准线x0的夹角，称为舷角;vt和vm分别是鱼雷和目标的速度;ηt和ηm分别是鱼雷和目标速度向量与视线的夹角，称为提前角或前置角;ψt和ψm分别是鱼雷和目标的弹道偏角，将鱼雷和目标视为质点时，它们也是鱼雷和目标的航向角。

2 鱼雷运动数学模型

所建立的反鱼雷鱼雷模型是在雷体坐标系下无横滚的侧向运动方程，反鱼雷鱼雷的自导航速V=60kn，角速度 ωy=45°/s，俯仰角设为零，数学模型如下:

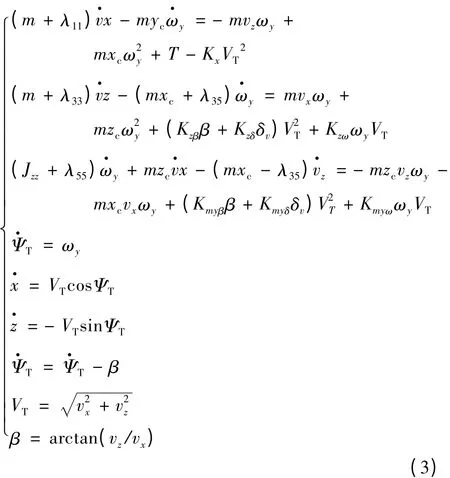
式中:m、vx、vz、β、ωy、δv、ΨT、VT、x、z、xc、zc、T 分别为反鱼雷鱼雷质量、X向速度、Z向速度、侧滑角、回旋(偏航)角速度、偏航(垂直)舵偏角、航向角、弹道偏角、速度、地面坐标系的X轴坐标和Z轴坐标、X向浮心、Z 向浮心、推力。λ11、λ33、λ35、λ55分别为雷体各个方向上的附加质量。Kx、Kzβ、Kzδ、Kmyβ为位置力及力矩的有量纲系数，Kzω、Kmyδ、Kmyω为阻尼力及力矩的有量纲系数。发射角设定为 －150°。

来袭鱼雷自导航速 Vt=40kn，角速度 ωt=15°/s，其数学模型与反鱼雷鱼雷一致。

3 弹道仿真实现

在仿真过程中，作出以下假设:

1)来袭鱼雷，反鱼雷鱼雷和舰船都视为质点，忽略体积弹性;

2)整个导引系统具有理想的控制、制导系统;

3)不计波浪的影响。

设目标舰船在探测到来袭鱼雷前以航速为15kn的速度进行直航行进，当来袭鱼雷进入到报警距离内后，以25kn的航速进行直航避规同时发射反鱼雷鱼雷进行拦截。

基于反鱼雷鱼雷攻击时间短，全弹道精确导引和一次性攻击，没有机会进行再搜索的弹道特点，弹道设计分为两段:初始搜索段和导引段。由于攻击时间短，要求反鱼雷鱼雷在出管后迅速完成寻深，并转向设定主航向，完成一次转角。到达设定主航向后即进入直航搜索段。反鱼雷鱼雷采取直航搜索的方式既满足了攻击时间段的需要，同时也能保证对来袭鱼雷的发现和攻击。

在反鱼雷鱼雷自导系统在850m范围内发现来袭鱼雷后，即进入自导段。由于反鱼雷鱼雷与来袭鱼雷呈迎击姿态，相对速度较大，采取提前角导引法将有利于保证导引效果，取提前角 ηt=15°。当与目标距离小于2m时，视为遭遇。

来袭鱼雷自导系统在1500m范围内发现舰艇后进入自导段，同样采取以提前角ηl=15°的固定提前角导引法进行追踪自导，直到与舰艇距离小于8m时，视为遭遇。

若始终未发现目标，则反鱼雷鱼雷与来袭鱼雷直航直到燃料耗尽。若发现目标后丢失，则在丢失方向上做直航搜索。

4 仿真结果

根据鱼雷数学模型以及固定提前角制导原理，采用Matlab/SimuLink[6]软件编写程序。采用变积分步长的4阶 Runge.Kutta法仿真，最小步长为0.01，最大步长自动调节。设置好各模块仿真参数后，即可开始进行仿真。反鱼雷鱼雷、来袭鱼雷与舰艇的仿真弹道曲线如图1所示。

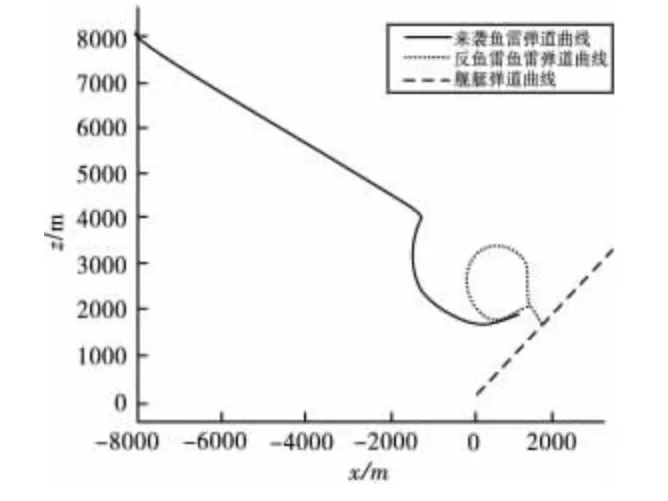
图1 反鱼雷鱼雷拦截曲线

通过曲线可以看出，反鱼雷鱼雷在被舰艇发射后，经过直航搜索段，在与来袭鱼雷相对距离850m时探测到对方，进入固定提前角导引段，后与来袭鱼雷遭遇，整个过程约为481.8s，终端脱靶量为终端时刻对应的最小距离1.979m。可以看出，固定提前角导引法的弹道前段较弯曲，需要绕到目标的尾后，需用法向过载较大;而弹道后段较为平直接近于直线，此外，反鱼雷鱼雷接近目标时的舷角不等于零，从而增大了目标的有效尺寸。因此，固定提前角导引法有较强的追踪能力，对于不同的机动目标都可以表现出很高的追踪效率，可以广泛应用于实际追踪问题中。

5 结果分析

下面通过分析仿真结果，比较提前角、发射角以及鱼雷速度对于导引弹道的影响。

5.1 反鱼雷鱼雷速度对于遭遇时间的影响

通过分别改变M文件中反鱼雷鱼雷推力以及来袭鱼雷推力的大小，得出一系列的时间值，如表1～表2所示。

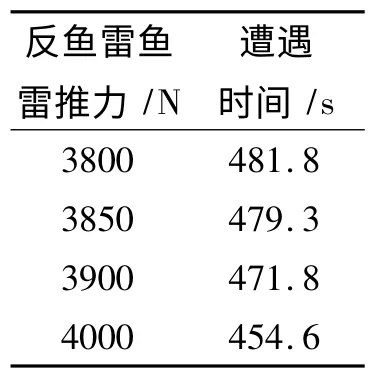
表1 反鱼雷不同推力值下的遭遇时刻表

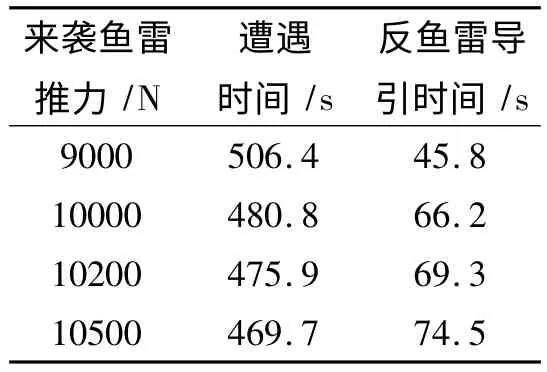
表2 来袭鱼雷不同推力下遭遇时间、反鱼雷导引时间表

由表1～表2可以看出，遭遇时间随着反鱼雷发动机推力的增加而减小，这是因为反鱼雷鱼雷的航行速度不断增大，导引时间减小，这样可以减小反鱼雷鱼雷的航程消耗。遭遇时间随着目标速度的增加而减小，而反鱼雷鱼雷导引段时间却不断增大。

5.2 发射角对于反鱼雷鱼雷弹道的影响

通过改变M文件中的反鱼雷发射角的大小，得到了一系列弹道曲线图。如图2所示。

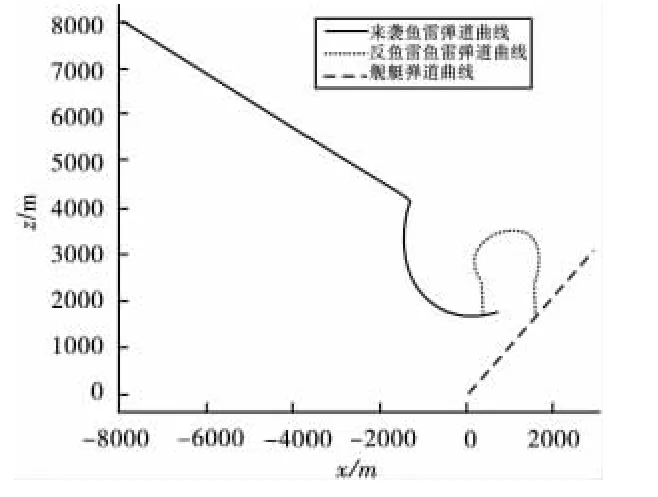
图2 发射角 －90°弹道曲线图

由图可以看出，随着发射角由 －90°减小到－180°，自导段弹道明显缩短，拦截时间不断减小。这说明发射角的选择对于拦截过程的影响十分明显，发射角越小，导引时间短，可以减小鱼雷的航程消耗，但弹道曲率半径大，对鱼雷机动性要求高;发射角越大，弹道曲率半径大，则对鱼雷机动性要求小，但导引时间长。所以，对机动性和导引时间之间的要求是相互矛盾的，应该折中考虑。

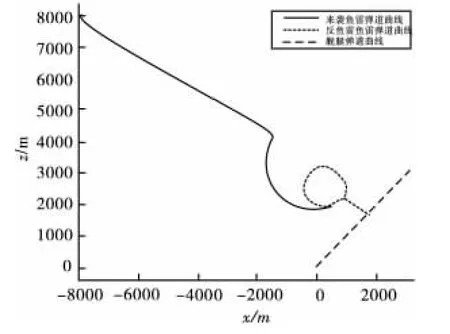
图3 发射角 －120°弹道曲线图

图4 发射角 －150°弹道曲线图

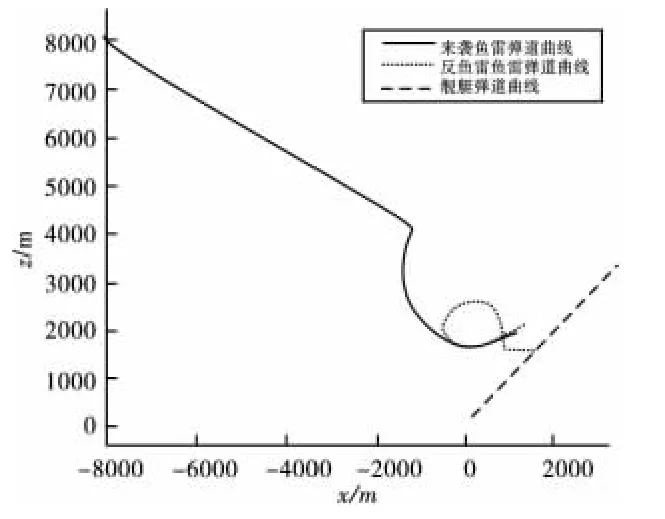
图5 发射角 －180°弹道曲线图

5.3 改变提前角对于反鱼雷弹道的影响

通过改变M文件中提前角的参数，得出一系列的弹道曲线图，如图6所示。

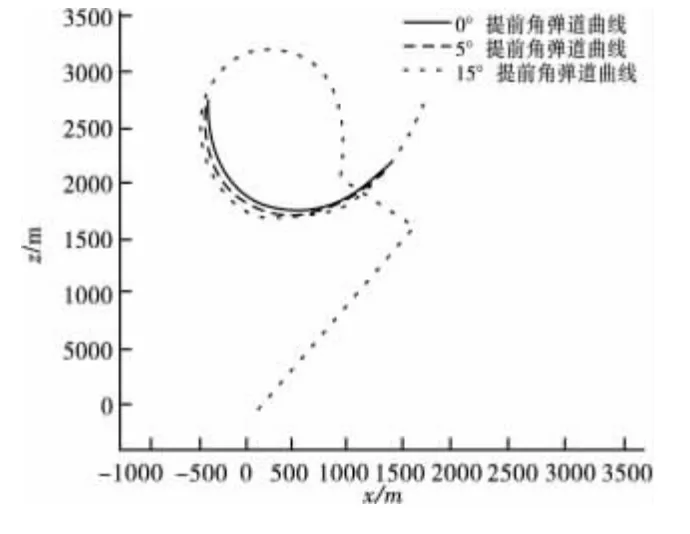
图6 不同提前角弹道曲线图

由图6可以看出，弹道曲率ρ随着提前角的增大而减小(弹道越来越平直)。随着反鱼雷鱼雷的弹道曲率变小，此时反鱼雷的最大承受过载能力要求降低。由此可以推出，取不同的提前角值，所得到的导引弹道就不相同。如果已知初始舷角q0，根据相对运动方程和固定提前角导引法的约束方程，可按式(4)确定提前角，使导引弹道趋向直线。

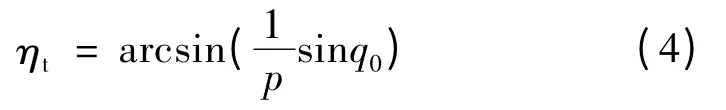
式中p为反鱼雷速度与来袭鱼雷速度之比。所以在提前设置提前角时，应尽可能将值设定与该预估值相近，这将有利于减小弹道过载。这个前提是在小提前角)的前提下得到的。对于大提前角的情况下，当鱼雷接近目标时弹道的需用法向过载很大，因而没有多大实际意义。

采用蒙特卡洛法，可得到鱼雷采用固定提前角导引弹道的脱靶量的统计结果，通过改变战术姿态等参数，得到 30 次仿真的脱靶量 ri(i=1，2，...，30)(数据略)。计算30次仿真的脱靶量均值m和方差σ2按下式计算:

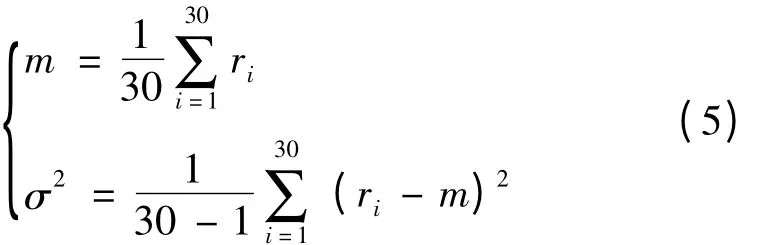
脱靶量均值m=1.9706m，脱靶量均方差 σ =0.0760m2，置信区间为m ±λσ，当作30次仿真统计试验时，对应于概率为95%，λ，则置信区间为[1.9422，1.9990]。

6 结论

结合文中的仿真结果表明，采用Matlab对反鱼雷鱼雷导引弹道仿真，通过简单建模，适当改变文件中的相关数据和参数，就可以对反鱼雷鱼雷在不同工况下的运动规律进行研究。仿真结果表明，反鱼雷鱼雷采用固定提前角导引律可以有效拦截来袭鱼雷，具有较强的追踪能力。同时提高反鱼雷鱼雷的航行速度可以明显缩短拦截时间，而较高速度的来袭鱼雷将会增加反鱼雷鱼雷的追踪难度。根据来袭鱼雷的方位，选择合适的发射角以及提前角，都可以大幅度提高反鱼雷鱼雷的拦截能力。文中的系统建模以及仿真方式，也完全适用于其他自导武器等动态系统的仿真研究。

[1]陈春玉.反鱼雷技术[M].北京:国防工业出版社，2006.

[2]钱东，张起.欧洲反鱼雷鱼雷研发展望[J].鱼雷技术，2006，14(5):8 －11.

[3]严卫生.鱼雷航行力学[M].西安:西北工业大学出版社，2005.

[4]何心怡，肖庆生.反鱼雷鱼雷自导方式研究[J].鱼雷技术，2010，18(1):21 －25.

[5]LI Wen-zhe，ZHANG Yu-wen. Torpedo’s automatically adjust lead angle guide trajectory simulation based on simulink[J].系统仿真学报，2009，21(10):3003 －3005.

[6]康凤举.现代仿真技术与应用[M].北京:国防工业出版社，2001.