旋转运动对聚能射流形成的影响数值模拟*

李如江，卢志燕，方志坚，孙素杰

(1中北大学化工与环境学院，太原 030051;2中国兵器工业第52研究所，山东烟台 264003)

0 引言

旋转稳定式破甲弹为了达到飞行稳定和提高打击精度，必须使其在弹道上始终保持高速旋转，例如美152mmXM409E5式多用途破甲弹，法国的105mm坦克炮用G型破甲弹等采用了线膛炮发射，其转速达到了6800～12000r/min。此外，对于尾翼稳定的破甲弹，为了减少火箭推力偏心和气动力偏心的影响，保证射击精度，飞行中也要求低速旋转。在破甲弹旋转过程中，药型罩和装药也同时获得一定的转速，当药型罩闭合时，根据动量守恒定律，射流将获得更高的转速。在离心力的作用下，射流可能发生径向离散，使射流分散、紊乱，严重影响了其侵彻性能。因此国内外针对旋转对破甲性能的影响进行了大量的试验研究。

早在20 世纪60 年代，Singh[1－2]借助 X 光测试手段，研究了旋转速度对射流形成的影响，基于理想不可压缩流体理论，给出了旋转速度对侵彻深度影响的理论计算公式。此后，研究人员通过改变药型罩结构和制造工艺来消除或减弱旋转对射流侵彻性能的影响，Pugh[3]通过在接近药型罩口部区域采用内外表面错位改善了形成射流的抗旋性能。Koch等[4]人对内表面错位非对称药型罩进行了试验研究，并通过二维数值模拟对其旋转补偿机制进行了分析。Wiener[5]等使用高精度、汇聚成像高速摄像机对旋压成型药型罩的压垮、聚能射流形成和延伸过程进行了试验研究，发现射流形成过程中存在着旋转，并对射流的角速度进行了测定。Schwartz等[6]对旋压药型罩的旋转补偿机理进行了研究。Silvestrov[7]通过试验研究发现提高药型罩材料抗拉强度可以延长旋转作用下射流的断裂时间。Ugrcic[8]使用有限元软件，假设射流为简支锥形长杆，沿整个长杆赋予相同的旋转速度，研究了角速度对射流临界破碎应力的影响，模拟结果显示，在射流的尾部区域最先达到临界应力，且射流明显变短，但是模拟条件与射流的实际形成过程显然不符。

随着计算机技术的飞速发展，采用动力有限元软件进行数值模拟为深入研究聚能射流的相关性能提供了重要的手段。文中利用LS-DYNA3D有限元软件，通过数值模拟研究了旋转速度对聚能装药射流的速度、形态以及偏心起爆与旋转运动的耦合对射流形成的影响。

1 有限元模型和计算参数

采用非线性动力学有限元软件LS-DYNA3D对旋转聚能装药数值建模。为简化计算，有限元模型仅由药柱、药型罩和空气三部分组成，采用多物质欧拉法进行计算。其中聚能装药的口径为36mm，药型罩口部壁厚为1mm，锥角为60°。起爆方式为点起爆。建模时对药柱和药型罩施加初始角速度以使其在形成射流过程中旋转，在空气边界处施加无反射边界条件以消除边界效应。有限元模型如图1所示。

图1 有限元模型

聚能药柱所用炸药为8701炸药，采用高能燃烧材料模型和JWL状态方程来描述。

式中:V= ρ0/ρ;E= ρ0e;ρ0是炸药初始密度，ρ 是爆轰产物密度，e是内能;A、B、R1、R2和 ω 为输入参数。相关计算参数为:ρ0=1.685g/cm3，D=8130m/s，A=625.3，B=23.29，R1=5.25，R2=1.6，ω =0.28。

药型罩材料为紫铜。聚能射流的形成和高速延伸经受了高应变率下的塑性变形，材料的屈服应力具有较强的应变硬化、应变率强化以及热软化效应。使用Johnson-cook模型和Grüneisen状态方程来描述。

采用Grüneisen状态方程。在压缩状态下:

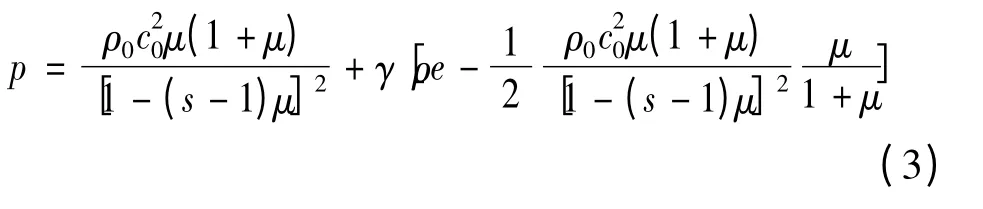
式中:μ = ρ/ρ0－ 1，ρ/ρ0为当前体密度与初始体密度的比值;c0、s为us-up直线截距和斜率，γ是Gruneisen系数，a是对γ的一阶体积修正量。相关计算参数为:ρ =8.96g/cm3;G=47.7GPa，A=90MPa，B=292，n=0.31，C=0.025，m=1.09，c=3940m/s，S1=1.49，γ =1.99。

空气采用空物质材料模型，通常把空气视为理想气体，密度为1.25×10－3g/cm3。状态方程采用多线性状态方程描述。

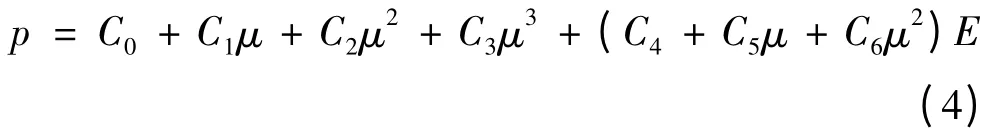
式中:μ = ρ/ρ0－ 1，C0=C1=C2=C3=C6=0，C4=C5=γ－1，γ为比热容。

2 模拟结果及分析

2.1 旋转速度对射流形成的影响

模拟了 0r/min、4000r/min、8000r/min、16000r/min四种初始角速度下聚能装药射流的形成过程。其中装药不旋转时形成的射流头部速度为5.95mm/μs，在其它三种旋转速度下射流的头部速度分别为5.919mm/μs、5.866mm/μs、5.7mm/μs，分别比不旋转时降低了 0.5%、1.41%和4.2%。以转速为横坐标，速度为纵坐标作图，可得旋转条件下射流的头部速度随装药转速的变化关系(见图2)。可以看出转速小于4000r/min时，射流头部速度降并不明显，随着旋转速度的增加头部速度下降较快，呈非线性降低。

图2 旋转速度和射流头部速度关系

图3给出了t=35μs时射流的形态比较。可以看出随着装药旋转速度的增加，射流头部到达y轴位置依次减小，由于旋转使头部速度减小原因所致。与传统观点相反，随着装药旋转速度的增加，射流的直径变细而不是变粗，无旋转时射流直径为2.5mm，而转速为16000r/min时射流直径约为1.5mm，由于聚能装药的高速旋转，药型罩口部附近的微元不能正常到达轴线形成射流，导致形成射流质量减少，当头部延伸到相同位置时，射流直径必然变细。射流直径变细，延伸过程中容易失稳断裂，不利于射流的侵彻。杵体直径变细，射流尾部直径变粗，在射流尾部区域附近应力最大，最先出现破碎，此点与文献[8]模拟结果相似。

图3 不同旋转速度条件的射流形态

随着转速的增加，射流长度变短，原因有两个，一是装药的高速旋转使形成的射流头部速度降低，二是从理论分析可知，药型罩口部附近微元在向轴线汇聚碰撞过程中，转速会进一步增加，高速旋转的微元会产生较大的离心力，同时口部装药厚度变薄，造成爆炸冲击波和产物驱动微元运动速度降低，当离心力大于其内向力时，药型罩口部附近微元将很难汇聚到轴线形成射流，模拟结果见图3(d)。

2.2 旋转运动和偏心起爆耦合对射流形成的影响

由于受生产和研制工艺水平限制，不可能保证聚能装药部件制造和组装过程做到严格对称。影响聚能装药性能的不对称因素主要包括药柱密度不均或其它瑕疵、药型罩和壳体的几何形状不对称、起爆系统偏置等。文献[9]曾对此结构的聚能装药在偏心距离(eccentric distance，ED)为1mm条件下，对射流的形成进行了X光测试和数值模拟对比，发现其之间符合良好。文中以偏心起爆为例，研究旋转运动和非对称的耦合作用对聚能射流形成的影响，设聚能装药的旋转速度为ω=16000r/min。

模拟结果如图4所示，其中图4(a)为ED=1mm，t=30μs时射流的状态，图4(b)、图4(c)和图4(d)分别为t=30μs、35μs和 38μs时旋转装药形成射流的状态。对比图4(a)和图3(a)可以看出，偏心起爆条件下随着射流的延伸，射流前部直径逐渐变细，射流保持了圆柱形状态，表面比较光滑，无颈缩和断裂现象。在100mm处的射流直径约为2.5mm，射流偏离了轴线约 1.15°。

比较图4(a)和图4(b)看出，当t=30μs时，旋转和偏心起爆的耦合作用对射流形成的影响更加严重，射流的头部速度为5.65mm/μs，比仅旋转条件下的射流头部速度降低了0.05mm/μs。射流的中后部出现了扁平扭曲现象，直径变粗，射流头部偏离轴线程度降低。

对比图4(b)、图4(c)和图4(d)可以看出，随着射流的延伸，射流后部的扁平扭曲现象更加严重，在射流轴线处出现了分叉现象，即逐渐分成两股射流。与模拟结果不同，传统观点认为在高速旋转作用下，射流会出现中空现象。在外界高速旋转下，其范围沿射流迅速扩展，并被甩向两侧，同时射流前部也出现了颈缩和断裂。射流在此状态下侵彻性能会迅速降低。图4(e)为Weickert[10]对某口径的旋转聚能装药射流的X光测试结果，射流头部偏向了另一侧，呈典型的偏心起爆状态，在射流的中后部出现了分叉现象(如箭头所示)。对比图4(e)和图4(d)，模拟结果和试验结果趋势符合良好。

图4 模拟结果对比

图5给出了射流中后部变化的局部放大图，从图上可以清楚看出药型罩口部微元形成了多层层裂和破片，在高速旋转作用下未能汇聚到轴线上。射流中后部的变化经历了变扁、心部开裂以及形成了两股射流等过程(见图5)。对比旋转以及旋转与偏心起爆模拟结果可以看出，采用精密装药有助于减弱旋转对其射流稳定性的影响。

图5 射流中后部分叉过程

3 结论

旋转聚能射流在轴向应力(由于速度梯度的存在)和离心力(由旋转速度和射流的直径变化决定)的耦合作用下处于一个复杂的应力－应变状态，特别是旋转和非对称因素的耦合使其受力状态更加复杂，相关理论模型直到现在还没有建立。文中利用数值模拟方法，研究了旋转以及旋转与偏心起爆的耦合对聚能射流形成的影响，对于此结构的聚能装药，得出如下结论:

1)数值模拟结果显示，旋转对射流的形成有重要影响。当旋转速度为4000r/min时，影响不显著，当转速为16000r/min时射流头部速度降低了4.2%。随着装药旋转速度的增加，头部速度下呈非线性降低，射流和杵体直径变细，射流长度变短。

2)旋转和非对称因素的耦合对射流的形成有严重影响。当旋转速度为16000r/min，起爆系统偏置1mm时，射流头部速度会进一步降低，射流的中后部出现了扁平扭曲现象，直径变粗，随着射流的延伸，逐渐分成两股射流，并迅速被甩向四周。

3)采用精密成型聚能装药可有效降低旋转对射流稳定性的影响。

[1]Singh S.A note on penetration by rotating shaped charges[J].Proc.Phys.Soc.1958，71(3):508 －512.

[2]Singh S.Penetration by rotating shaped charges[J].J.Appl.Phys.1960，31(3):578 － 581.

[3]Koch A，Jaggi P，Jaun W，et al.Study of spin-compensated shaped charges[C]//19th International Symposium of Ballistics，Interlaken，Switzerland，2001:1501 －1508.

[4]Pugh，Eichelberger. Fluted liners for shaped charges，US，3726224[P].1973.

[5]Wiener K，Shaw L，Muelder S，et al. Dynamic behavior of a shear-formed shaped-charge liner[J]. Propellants，Explosives，Pyrotechnics，1993，18(6):345 － 351.

[6]Schwartz A J，Busche M J，Becher R，et al. Role of texture in spin formed Cu shaped-charge liners[C]//19th International Symposium of Ballistics，Interlaken，Switzerland，2001:1501－1508.

[7]Silvestrov V V，Gorshkov N N. Effect of the strain rate on the tensilestrength of a copper shaped-charge jet[J].Combstion，Explosive，and Shock Waves，1997，33(1):93－99.

[8]Ugrcic M，Maksimovic S.Critically shaped charge jet stress caused by angular velocity[J]. FACTA UNIVERSITATIS，Series:Mechanics，Automatic Control and Robtics，2007，6(1):119－130.

[9]李如江，张晋红，王建波，等.偏心起爆对射流形成的影响[J].弹箭与制导学报，2012，32(1):85 －88.

[10]Walters W P，Zukas J A. Fundamentals of shaped charges[M].New York:John Wiley and Sons，1989:330－332.