基于均匀设计的UHMWPE纤维拉伸蠕变性能的测试方法

王新威，张玉梅，王 萍，侯秀红，徐静安

(1.上海化工研究院技术开发中心，上海200062;2.上海市聚烯烃催化技术重点实验室，上海200062)

蠕变现象普遍存在于有机纤维的应用过程中。超高相对分子质量聚乙烯(UHMWPE)纤维分子链长，分子间作用力小，在应力作用下更易产生分子间滑移，蠕变现象相对突出，应用时出现尺寸、形态的不稳定［1－2］。

目前，UHMWPE纤维蠕变性能测试参照GB/T 19975—2005《高强化纤长丝拉伸性能试验方法》。该标准规定实验的有效夹持长度至少为200 mm，施加负荷包括初负荷和重负荷，初负荷为(0.05 ±0.01)cN/dex，重负荷规定为断裂负荷的5%，10%，20%等，加载时间即重负荷终止时间为 1 min，5 min，30 min，1 h，4 h，8 h，24 h 或至断裂等。这些规定还没有完全确认测试参数，没有提到由初负荷加载到重负荷过程中的拉伸速度以及这一过程所发生的试样尺寸变化，因此还需确定各参数的数值以及蠕变性能指标，才能对高强纤维的蠕变性能进行准确评价。

将蠕变伸长率(G)分成两个部分:一是蠕变载荷从初负荷到重负荷这一区间的试样伸长率叫预伸长率(G0);二是到达重负荷后在设定时间(蠕变时间)内的试样伸长率叫定载荷伸长率(G1)。其中，蠕变载荷从初负荷到重负荷的这段时间内拉伸速度的大小对G有重要影响。作者在前期研究的基础上［3］，采用均匀设计试验、多项式回归等研究手段确定了UHMWPE纤维蠕变性能的测试方法。

1 实验

1.1 试样及仪器

UHMWPE纤维:线密度为1 544 dtex，断裂强度27 cN/dtex，市售;DLL-5000型电子式拉力机:上海德杰仪器设备有限公司制;Y331A-II型纱线捻度仪:南通宏大实验仪器有限公司制。

1.2 实验方法

将测试的UHMWPE纤维试样在温度(20±2)℃、相对湿度(65±3)%的标准大气条件下平衡48 h;在该环境条件下使纤维试样加捻，剪取纤维的测试长度，后将试样的一端夹入夹持器，另一端不解捻地夹入另一夹持器中。施加预张力(初负荷)(0.05 ±0.01)cN/dex后，在一定拉伸速度下逐渐施加蠕变负荷，蠕变载荷数值为纤维断裂负荷的10%，20%，30%，40%等。到达蠕变载荷时，观察并记录试样的G0后，维持一定的蠕变时间，观察并记录试样的G1。G计算公式如下:

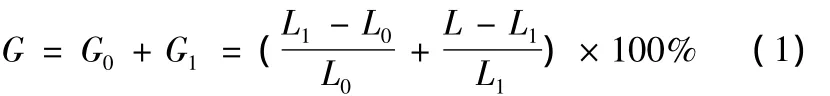
式中:L0为试样的初始长度;L1为达到重负荷时试样的长度;L为加重负荷后一定蠕变时间后试样的长度。

2 结果与讨论

2.1 实验设计

通过单因数实验和正交试验等，考察发现测试过程中蠕变载荷、拉伸速度、蠕变时间、纤维测试长度是影响测试结果的主要因素。以蠕变载荷、拉伸速度、蠕变时间、纤维测试长度为自变量，蠕变伸长率为应变量，采用均匀设计的方法进行测试，对测试结果采用线性回归的方法进行处理，最终得出UHMWPE纤维拉伸蠕变率测试的合理参数。即所测G大于1.0%，变异系数小于10%，数据稳定。

采用4因素10水平进行实验，即U10(103×5)均匀设计表进行设计［4］，再用DPS数据处理系统对其结果进行多项式逐步回归，分析得到回归模型，并进行验证。

2.2 均匀设计结果

从表1可看出，纤维的G值大小合理，变异系数普遍低于10%，但其中实验7，9，10在未达到设定蠕变时间的时候，纤维即发生断裂，没有按照设计的因素完成实验，属于“突变点”，不能与其实验的结果进行二次多项式回归处理。选择不使纤维断裂的条件继续设计U6*的均匀设计表进行测试，如表2所示。由表2可看出，所得测试结果合理，G大于1.0%，变异系数小于10%。

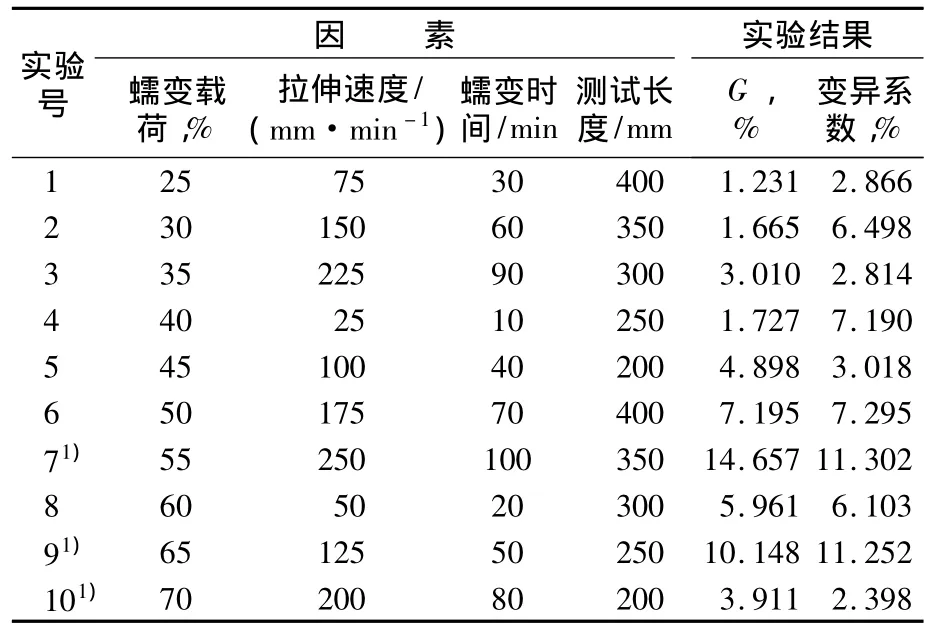
表1 U10(103×5)均匀设计及其结果Tab.1 U10(103×5)uniform design and results

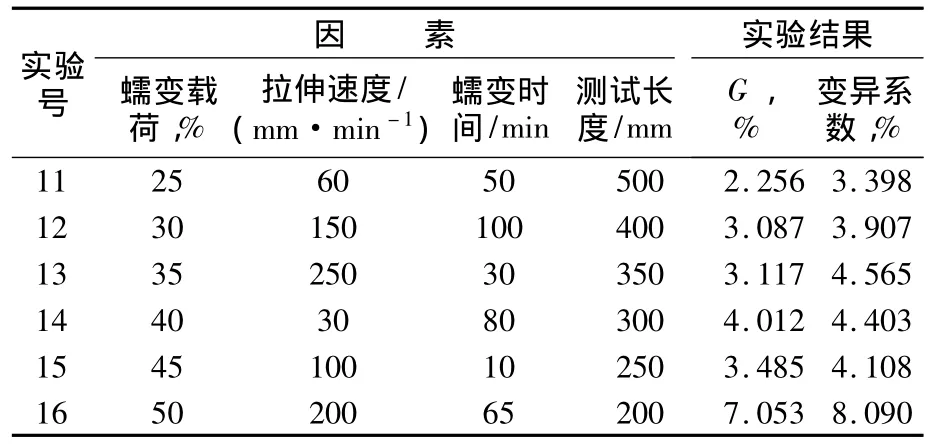
表2 U6*均匀设计表及其结果Tab.2 U6*uniform design and results

根据表1和表2，应用DPS分析软件对2次均匀设计的有效结果进行二次多项式逐步回归:

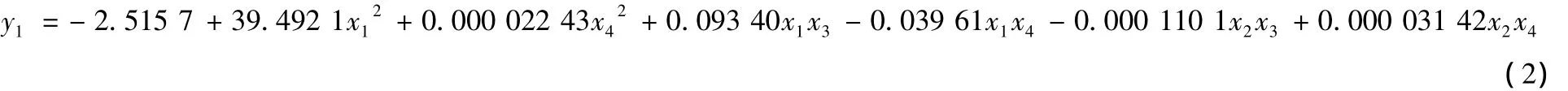
式中:x1为蠕变载荷;x2为拉伸速度;x3为蠕变时间;x4为测试长度;y1为蠕变伸长率。

对回归模型进行显著性检验，如表3所示。结果表明回归模型能够很好的拟合UHMWPE纤维拉伸蠕变率的测试过程。

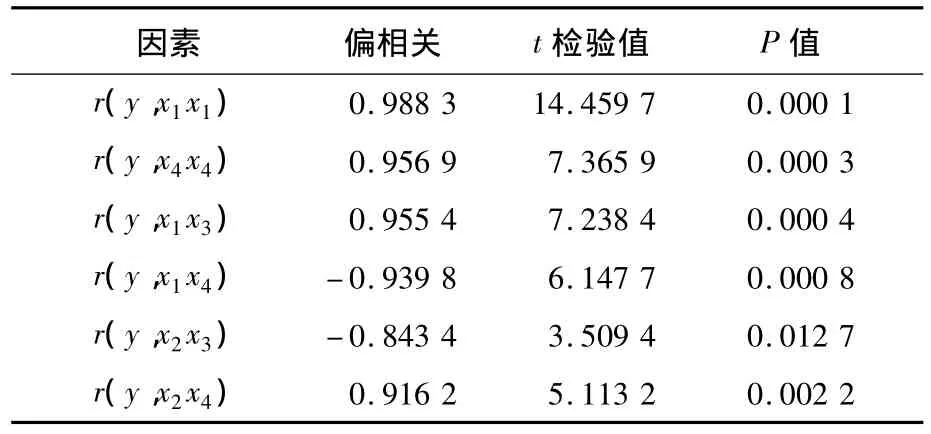
表3 回归模型的显著性检验结果Tab.3 Significance test results of regression model

回归方程的相关系数(R)为0.996 8，F值为 127.730 6，显著水平(P)值为 0.000 1，剩余标准差为 0.233 9。

从回归模型得出优化的蠕变性能测试参数，其自变量为 x1，x2，x3，x4的优化值分别为 210(50%)，197.670 5，70.917 2，200.481 9，G 的模型预测值为7.301 5%。

因此，对于此UHMWPE纤维G的测试，选取x1为纤维断裂载荷的50%，x2为200 mm/min，x3为70 min，x4为200 mm，所得G为7.012%，与模型预测值接近。

3 结论

a.采用U10(103×5)、U6*等2次均匀设计试验，研究了1 555 dtex的UHMWPE纤维拉伸蠕变性能的测试方法。

b.对实验结果采用多项式回归的方法进行处理，建立了拉伸蠕变性能测试结果的回归模型，回归模型的R达到0.996 8，对模型得出的测试参数优化值进行试验验证，发现因变量的模型预测值与实测值有较好的对应，表明回归模型具有较好的拟合性和稳定性，可以通过此参数进行1 555 dtex的UHMWPE纤维蠕变性能的测试。

［1］樊愈波.超高相对分子质量聚乙烯长丝蠕变性能的研究［J］.合成纤维，2011，40(l):28 －32.

［2］徐明忠.超高分子量聚乙烯纤维蠕变性能研究进展［J］.合成纤维工业，2012，35(2):44 －47.

［3］张玉梅，王新威，王萍，等.UHMWPE纤维拉伸蠕变性能的测试方法研究［J］.合成纤维工业，2013，36(3):71 －73.

［4］潘丽军，陈锦权.试验设计与数据处理［M］.南京:东南大学出版社，2008:165 －190.