基于总体最小二乘的改进GM（1，1）模型及其在建筑物沉降预测中的应用

袁 豹，岳东杰，李成仁

（河海大学 测绘科学与工程系，江苏 南京 210098）

灰色系统理论是研究系统分析、建模、预测、决策和控制的理论。利用灰色数列预测方法可以实现对系统的时间序列数量大小的预测，即对系统的主行为特征量或某项指标发展变化到未来特定时刻出现的数值进行预测。灰色系统理论及其动态GM模型已经广泛用于社会经济等各个学科。1988年陈明东等首次在滑坡变形监测中采用灰色系统理论中的GM（1，1）模型，此后该模型在滑坡监测及相关变形监测工作中得到广泛研究和应用［1］。基于传统GM（1，1）模型中存在的一些缺陷，很多学者对此模型进行了改进。戴华将GM（1，1）和GM（1，N）模型联合应用于自来水厂的自动加矾系统［2］；汪凡等将灰色关联模型和主成分分析结合在一起应用于公司绩效评价和变形监测等领域［3－4］；李晓红提出以优化模型背景值为基础重构背景值的GM（1，1）模型［5］；靳晓光根据非等间距模型和优化背景值两个角度提出滑坡变形预测的普适灰色模型［6］；李秀珍等从改变模型背景值出发提出变形预测的中心逼近式GM（1，1）模型［7］。

上述GM（1，1）模型以及改进的GM（1，1）模型虽然在一定程度上提高了预测数据预测精度，但是都没有考虑模型本身的数据结构，且针对不同数学特点的变形数据，各改进模型的适用性有着一定的模糊性。针对传统模型在求解模型或参数或是模型背景值时都采用的最小二乘方法，没有能够顾及所建立的微分方程中系数矩阵和观测矩阵数据之前的自相关性，考虑采用总体最小二乘方法并对系数矩阵和观测矩阵予以定权来求解模型灰参数，这种方法更加严谨、科学，可以获得较为精确的预测效果。

1 GM（1，1）模型

假设有原始非负离散数列为x（0）＝｛x（0）（1），x（0）（2），…，x（0）（n）｝，n为序列长度（GM（1，1）模型处理的数据序列一般取等时间间隔序列，若原始数据为非等时间间隔序列，则可以采用线性插值或是等间距处理来保证模型具有较高的滤波精度，对x（0）序列数据进行一次累加生成（1－AGO）处理，得到 一 个 新 的 序 列x（1）＝ ｛x（1）（1），x（1）（2），…，x（1）（n）｝。

对x（1）建立一阶白化微分方程为

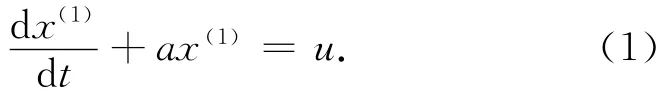
一般称式（1）为GM（1，1）一阶模型，式中：t为时间变量，a，u为待定灰参数，其白化值（即灰区间中可能的值）或者称为估计值为α∧＝［a，u］T。采用最小二乘平差法求得灰参数

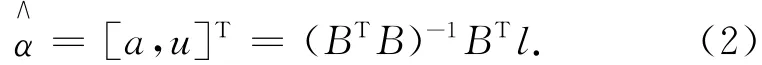
将灰参数代入微分方程，可得

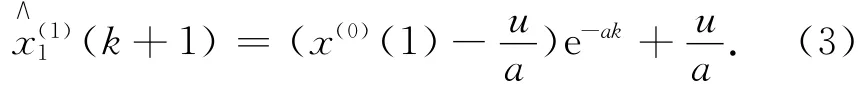
式中：e为常数，对（k＋1）进行一次累减生成，可得到还原数据

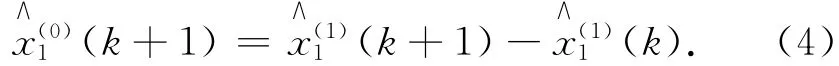
2 基于总体最小二乘的改进GM（1，1）模型

从上述GM（1，1）模型求解方法可以看出，在求解灰参数时采用的是最小二乘的方法，这样做的前提是假设系数矩阵B中数据不含有误差而只对观测值矩阵l进行改正。从系数矩阵B的数据结构

可以看出，系数矩阵中第1列数据是根据原始数据序列一次累加后的数据运算得到，如果原始数据含有测量的偶然误差，则系数矩阵B中第1列数据也含有测量误差，需要在平差时进行改正，这时就要采用能同时顾及系数矩阵和观测值矩阵，同时含有误差的总体最小二乘方法来求解模型灰参数。

2.1 总体最小二乘基本思想

针对线性方程组AX＝L，经典最小二乘的方法是在残差平方和极小的条件下求出参数的最佳估计值。该方法的前提之一是假定系数矩阵A是由没有误差的精确值组成的，而只对观测值L矩阵进行改正，事实上，观测向量、系数矩阵均有扰动，因此，从理论上讲应该同时考虑L和A的扰动才严密，这就是总体最小二乘（TLS）的基本思想［8］。总体最小二乘的函数模型可归结为

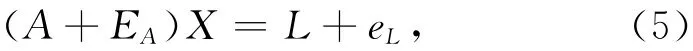
且有

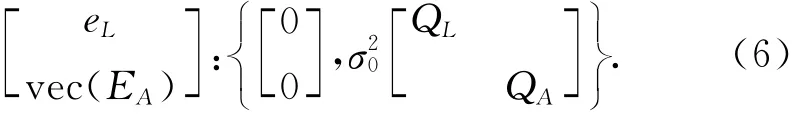
其中：A∈Rn×m，L∈Rn，X∈Rm，rank（A）＝m＜n，n为观测值个数，m为待估参数个数，QL和QA分别为eL和eA的对称非负定协因素阵，EA为系数矩阵的误差，eL为观测值阵的误差，误差矩阵属于相互独立的白噪声误差。这一模型称为EIV（Errors－in－Variables）模型。QA＝Q0⊗Qx，“⊗”表示矩阵之间的直积，即“Kronecker－Zehfuss积”，具体表现为：M⊗N＝［mijN］，M＝［mij］，vec（）表示矩阵的列向量化运算。QL，Q0，Qx，QA为非负正定协因素矩阵。在等权的情况下有：QL＝In，QA＝Im⊗In＝Inm，Qx＝In，Q0＝Im，一般称为总体最小二乘法（TLS）；不等权的情况下有：QL＝P－1L，QA＝Q0⊗Qx＝P－10⊗P－1x＝P－1A，Qx＝P－1x，Q0＝P－10，P0为系数矩阵A的列向量权阵，Px为系数矩阵A的行向量权阵［9］。加权总体最小二乘（WTLS）的准则为

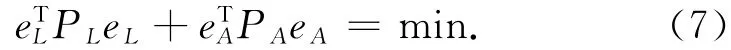
随机模型为

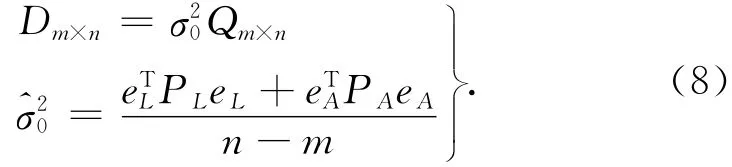
2.2 权阵的确定

与最小二乘平差方法一样，在总体最小二乘模型中当观测值数据之间不等精度或是不相互独立以及系数矩阵和观测值矩阵之间存在相关性时就要考虑采用加权总体最小二乘法，对系数矩阵和观测值矩阵予以定权处理。在加权总体最小二乘问题中，权阵的确定是一个重要的部分。

灰色模型在变形监测等数据预测领域中的应用，所要处理的数据对象大多是具有时间特性的独立数据，即时间序列数据是在不同时间点采用相同精度仪器或是相同采集方法获得的一些列数据，可以近似认为这些数据同精度，然而，GM（1，1）模型中系数矩阵中的数据来源于原始序列数据，若原始数据序列存在测量偶然误差，则系数矩阵必然受到这种误差的影响，即误差传递。假设系数矩阵B的协因数阵为QB，观测值矩阵l的协因数阵为Ql。设有 原 始 序 列 数 据x（0）＝ ｛x（0）（1），x（0）（2），…，x（0）（n）｝，根据分析可以认为σ1＝σi＝σn，其中σi（i＝1，2，…，n）表示该数据的中误差，则定义σ1为单位权中误差，则可知Ql＝I。根据系数矩阵B中数据所求得的计算方法，可知系数矩阵中的数据来源于原始数据的线性运算，采用协因数传播定律可以求出。则有P0＝Q0＋，Px＝Qx＋，P1＝Ql＋（＋表示伪逆），这样便可较为精确地确定系数矩阵和观测值矩阵的权阵，采用加权总体最小二乘方法求解参数。

2.3 改进GM（1，1）模型的确定

首先采用一次累加方法对原始序列数据进行处理，建立改进的GM（1，1）模型，此时可以表示为

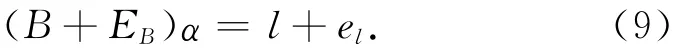
其中α＝［a，u］T。根据Burkhard Schaffrin与Andreas Wieser［10］提出的迭代解算方法，求解改进GM（1，1）模型灰参数的具体步骤如下：

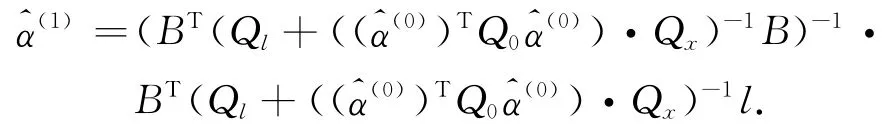
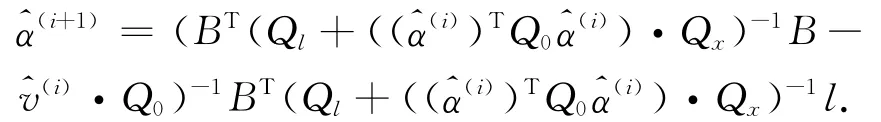
3）给定迭代限差δ0，重复2）直到，此时即为所要求得参数，并且计算单位权方差，观测值改正数和系数阵改正数。

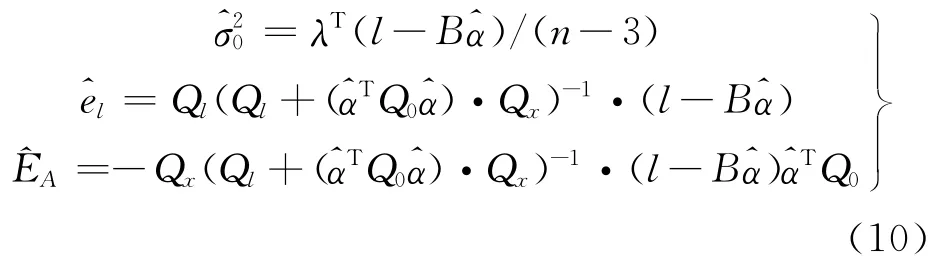
3 应用与实例分析

灰色理论模型近年来在滑坡预报以及经济、人口预测方面得到了一定的应用，通过引入总体最小二乘的方法来对GM（1，1）模型予以改进使得这一模型原理更加严谨，方法更加准确，应用更加广泛。改进的GM（1，1）模型将会受到各研究领域学者的关注并取得更加广泛的实际应用效果。

本文实例选取的是某一建筑物在施工期间测量得到的共18期的数据，检测周期为1周，利用前15期数据作为建模原始数据，后3期数据用于模型预测效果的检验数据。为了比较采用总体最小二乘法建立的改进GM（1，1）模型与传统GM（1，1）模型的区别，分别采用最小二乘（LS）和加权总体最小二乘（WTLS）方法求得模型灰参数，见表1。

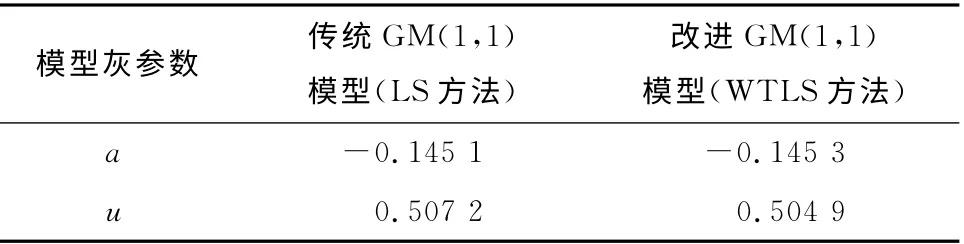
表1 模型灰参数结果

从模型灰参数来看，最小二乘法与总体最小二乘法有一定差别，比较最小二乘法与总体最小二乘法的拟合效果，计算出模型的拟合精度见表2。

表2 最小二乘法和总体最小二乘法的模型精度比较mm

建立准确的模型是为了掌握数据序列的变化趋势，发现数据序列的变化规律，以及更准确地预测下一个时刻的变形值，从而可以及时对建筑物的安全状态进行评价与预警，为监测工作的决策提供有效的依据。表3是利用已建好的GM（1，1）模型对监测点的16～18期沉降量进行预报的结果。

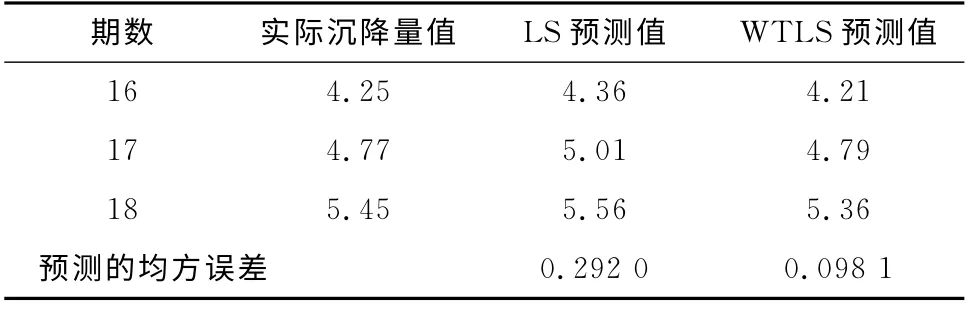
表3 沉降量预测 mm

从表3可以看出：采用总体最小二乘方法建立的改进GM（1，1）模型具有较好的预测效果，预测精度比传统的最小二乘方法高。为了直观比较最小二乘法与总体最小二乘法的优劣性，图1分别绘制出二者的沉降预测效果图。

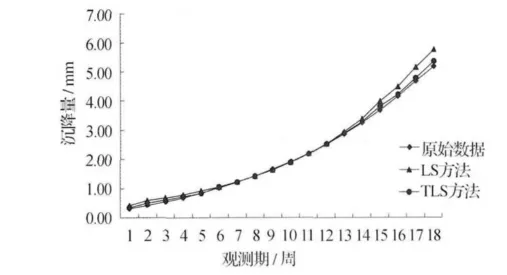
图1 最小二乘法与总体最小二乘法的预测效果比较

从图1可以看出，采用（加权）总体最小二乘法的模拟值和预测值与实际值的差别普遍比采用最小二乘方法的小，说明前者具有较小的预测误差，预测效果较好。

4 结 论

1）改进GM（1，1）模型灰参数求解的方法，采用严密的总体最小二乘法可以得到更高精度的模型灰参数，建立的改进GM（1，1）模型可以达到更高的模型与预报精度。

2）在采用总体最小二乘方法时，如若系数矩阵和观测值矩阵内部以及相互之间不独立或是存在数据相关性，则要考虑采用加权总体最小二乘法。

3）GM（1，1）模型适用于原始序列数据符合指数增长形式，适用性不足，对基于总体最小二乘方法的改进GM（1，1）模型做一些其他方面的改进，以使得灰色系统理论及动态GM模型达到更好的应用效果，还需要进一步研究。

［1］陈明东，王兰生.边坡变形破坏的灰色预报方法［C］//全国第三次工程地质大会论文选集（下）.成都：成都科技大学出版社，1988：1226－1232.

［2］戴华.GM（1，1）和GM（1，N）联合模型在自来水厂自动加矾系统预测中的应用［J］.湖北民族学院学报：自然科学版，2011，29（2）：152－156.

［3］汪凡，赵军.基于灰色关联模型和主成分分析的上市公司绩效评价研究［J］.商业经济，2011（3）：110－111.

［4］曹凯，许昌.GM（1，1）、GM（1，N）联合模型在建筑物沉降预测中的应用［J］.水科学与工程技术，2007（6）：54－57.

［5］李晓红，靳晓光，亢会明，等.GM（1，1）优化模型在滑坡预测预报中的应用［J］.山地学报，2001，19（3）：265－268.

［6］靳晓光，李晓红.边坡变形模拟预测的普适灰色模型［J］.中国地质灾害与防治学报，2001，12（2）：51－55.

［7］李秀珍，孔纪名，王成华.中心逼近式灰色GM（1，1）模型在滑坡变形预测中的应用［J］.工程地质学报，2007，15（5）：673－676.

［8］Golub G H，Van Loan C F.An analysis of the Total Least Squares problem［J］.SIAMJ Numer Anal，1980，17（6）：883－893.

［9］袁庆，楼立志，陈玮娴.加权总体最小二乘在三维基准转换中的应用［J］.测绘学报，2011，40（5）：116－117.

［10］Schaffrin B and Wieser A.On weighted total leastsquares adjustment for linear regression［J］.Journal of Geodesy，2008，82：415－421.