考虑荷载作用下抗力时变特性的沿海钢筋混凝土结构可靠度分析

崔衍强，王元战，王 军

（天津大学建筑工程学院港口与海洋工程天津市（教育部）重点实验室，天津300072）

海洋环境下的钢筋混凝土结构所处环境非常恶劣，在结构服役基准期内受水流冲刷，波浪潮流，大气腐蚀和冻融侵害等，同时结构物还承受着外部荷载的作用，使得钢筋混凝土结构容易发生钢筋锈蚀等抗力变化过程，严重影响了结构的正常使用状态和承载力极限状态。

工程结构物寿命周期可靠度分析的主要研究内容包括：在设计使用基准期内各种作用的随机过程、结构抗力的时变模型、考虑作用效应和抗力时变过程的可靠度分析方法等。作用的随机过程模型方面已开展了如风力随机过程、波浪长期分布概率模型等大量相关研究工作［1］。在结构抗力时变模型方面，已有学者研究了荷载对结构抗力的影响，如Francois和MASO等［2］最早研究荷载对氯离子的渗透和钢筋锈蚀的作用，得到荷载对其有明显的影响；Yoon等［3］研究表明加载方式和加载水平对钢筋锈蚀有显著影响；Chun Qing Li等［4］研究表明试件处于持续荷载作用下，氯离子渗透会加速，钢筋腐蚀时间会缩短；水金峰［5］、何世钦［6］进行了荷载作用对氯离子扩散影响机理的研究，得到了不同环境下的扩散方程；张德峰［7］采用Fick定律拟合了扩散系数与构件应力状态的关系；王元战等［8-9］在统计分析相关实验数据基础上，建立了考虑荷载影响的氯离子扩散模型和钢筋锈蚀模型，但是上述研究都没有在研究成果基础上进行结构的可靠度分析。在可靠度分析方法方面，赵国藩等［10］和牛荻涛等［11］，考虑抗力随机过程对大气环境下混凝土结构进行了可靠度分析，但是大气环境下与海洋环境下结构抗力随时间变化机理存在本质差别；王元战等［12］给出了高桩码头全寿命可靠度分析方法，但是没有考虑荷载作用对结构抗力随机过程的影响。

目前基于结构可靠度理论对工程结构物进行寿命分析的研究大都没有考虑荷载对结构抗力时变特性的影响。本文建立了荷载作用下的氯离子扩散模型和钢筋锈蚀模型，并以此为基础建立了海洋环境下考虑荷载作用的结构劣化随机过程模型，将其应用于港口与海岸工程结构可靠度分析，建立了考虑荷载作用下抗力时变特性的钢筋混凝土结构耐久性和承载力可靠度分析方法，可为新建结构的可靠度设计理论和已建结构的可靠度分析提供新的思路。

1 海洋环境下钢筋混凝土结构劣化的随机过程模型

海洋环境下钢筋混凝土结构的劣化过程是受环境侵蚀、荷载作用和材料随机性等影响因素耦合作用的结果，破坏过程十分复杂，影响因素众多，考虑所有影响因素建立结构抗力随时间变化的模型难度较大，同时实际工程应用也不方便，所以针对海洋环境钢筋混凝土结构承受荷载的特点，着重于结构发生劣化对结构承载力降低的影响，认为结构劣化有以下过程：氯离子扩散、钢筋锈蚀、锈蚀钢筋力学性能变化、混凝土强度变化、锈蚀钢筋混凝土构件粘结性能退化等。

1.1 荷载作用下的氯离子扩散模型［13］

海洋环境下钢筋混凝土结构劣化问题中，钢筋锈蚀问题至关重要，而氯离子是海洋环境下引起钢筋锈蚀的主要因素，以Fick第二扩散定律［14］描述氯离子在混凝土中的传输机理。

海洋环境下氯离子在混凝土中的扩散的最快方式是通过海水的毛细管吸收作用，而且实际沿海结构都承受着外部荷载的作用，构件都处于应力状态下，构件发生了微裂缝，加剧了毛细管的吸收作用。以系数形式考虑荷载作用，认为表面氯离子浓度是变化的，同时考虑氯离子扩散系数的时变特性、水灰比、温度、氯离子的结合能力、养护条件和环境等因素，并将各要素的影响以系数形式表示，进行推导得到海洋环境下，荷载作用下的氯离子扩散方程。时间影响参数按Mangat［15］提出的D（t）=D0（t0/t）α计算，考虑上述各影响要素后氯离子扩散系数可以表示成

式中：KR为氯离子在混凝土中吸附能力的影响系数；KT为温度影响系数；Kc为养护条件影响系数；Ke为环境影响系数；f（δ）为荷载系数；D0为在氯离子腐蚀环境中特定基准时间t0后的氯离子扩散系数；α为常数。考虑表面氯离子浓度时变特性的初始条件和边界条件为C（x，0）=C0=0；C（0，t）=CS（t）；C（∞，t）=C0。

经过推导，得到海洋环境下，考虑荷载作用的氯离子扩散模型

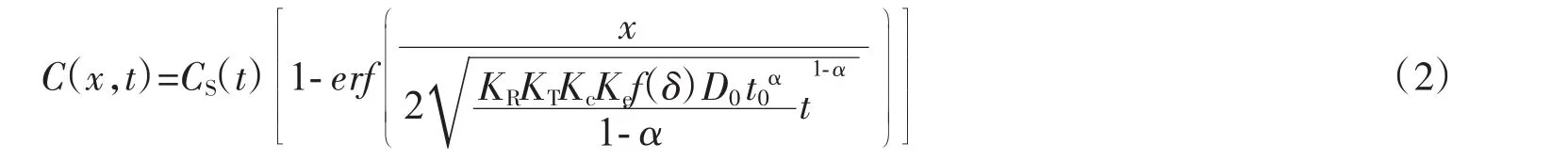
式中：erf（x）为误差函数，其他符号意义同前，模型中各参数取值如下。

（1）α取值。深入分析各种模型后，根据文献［16］建议取值如表1所示。

（2）荷载影响系数。王元战［8］在查阅大量文献资料的基础上，分别针对干湿交替、浸没在盐水中和盐雾腐蚀3种条件，根据相对应的文献［5-7］选定将荷载作用对Cl-扩散的影响系数进行总结，用f（δ）表示（表2）。

（3）水灰比与D0取值。氯离子在混凝土中传输受水灰比影响较大，水灰比越大，混凝土孔隙率越大，渗透和扩散速度越快。Bamforth和Price［17］给出了扩散系数和水灰比关系的经验公式

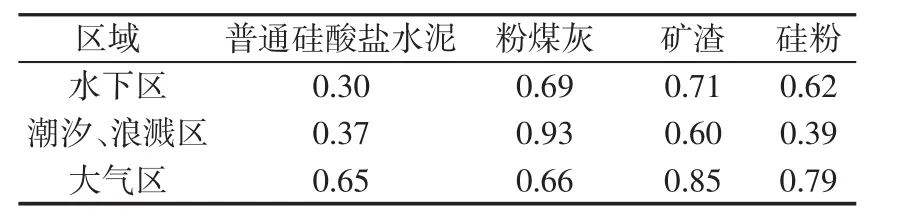
表1 α取值Tab.1 Value of α

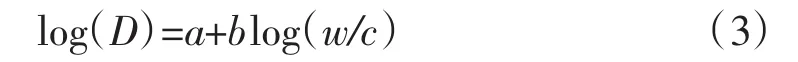
式中：a，b为经验系数，扩散系数单位为m2/s，由在以色列地中海1 a暴露试验数据得a=-10.8，b=1.9。将t0=1 a作为初始参照时间，则

表2 荷载影响系数Tab.2 Loading effect factor

（4）吸附修正系数KR。凝胶材料的吸附性能对扩散系数的影响以系数KR形式表示，采用线性理论计算，KR计算方法和取值范围参见施惠生等［18］研究。

（5）KT取值。Stephen等［19］给出了温度对于扩散系数影响的经验模型，参照其研究将温度影响因素定义为系数KT

式中：T1、T2为温度，单位为K；q为常数，由混凝土水灰比确定，q的建议值为当w/c=0.4时，q取6 000 K；当w/c=0.5，q取 5 450 K；当 w/c=0.6，q取 3 850 K。

（6）Kc与 Ke取值。本文基于文献［20-21］，通过统计整理数据，引入了环境修正系数Ke，如表3所示，养护修正系数Kc，如表4所示。

表3 环境修正系数KeTab.3 Correction coefficient of environment

表4 养护修正系数KcTab.4 Correction coefficient of concrete curing

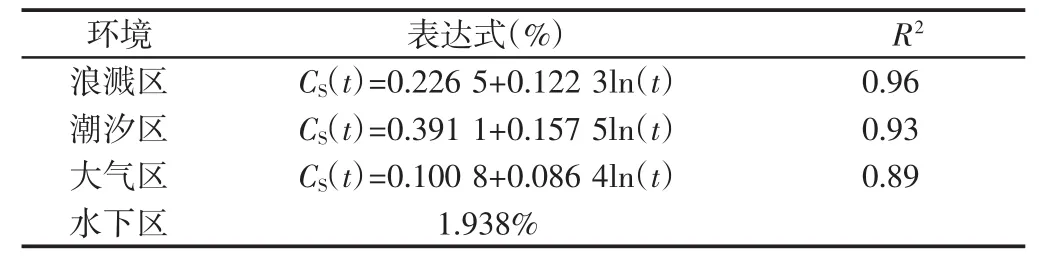
表5 表面氯离子浓度Cs（t）（混凝土质量百分比）Tab.5 Chloride concentration Cs（t）on surface of concrete member

（7）表面氯离子浓度Cs（t）。混凝土表面氯离子浓度决定了扩散过程的浓度梯度，对于扩散速度有很大影响，按照海洋环境下，混凝土构件所属的不同环境条件，采用最小二乘法拟合Costa和Appleton［13］的大量实验数据，得到表面氯离子浓度经验公式（表5）。

1.2 荷载作用下钢筋锈蚀模型

海洋环境下，钢筋混凝土结构开裂前和开裂后的锈蚀速率有明显的区别，开裂前、后采用不同的模型。

混凝土保护层开裂前，采用1.1节所述氯离子扩算模型修正Youping Liu模型［22］，得到荷载作用下的开裂前锈蚀模型

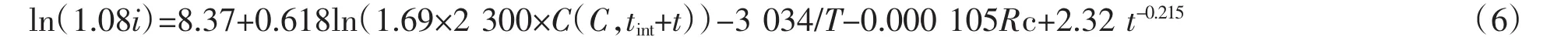
式中：i为锈蚀速率，μA/cm2；C（C，tint+t）是钢筋开始锈蚀后第t年的钢筋表面氯离子浓度；混凝土的重量取为2 300 kg/m3；tint为钢筋开始锈蚀时间，a；T为钢筋表面温度，K；t为锈蚀时间，a；Rc为混凝土保护层的电阻，ohms，若无实测数据，按照Rc=exp（8.03-0.549ln（1+1.69Ct））。式中Ct是保护层中氯离子浓度的平均值,kg/m3。

混凝土开裂后，钢筋锈蚀发展迅速，锈蚀速率变大，出于安全考虑选择保守的标准模型［23］。

模型综合表述如下

式中：λc1为钢筋在混凝土保护层开裂前的锈蚀速度，mm/a；λcl1为钢筋在混凝土保护层开裂后的锈蚀速度，mm/a；tcor为混凝土保护层开裂临界时间；i按照式（6）确定。

1.3 钢筋强度降低模型

混凝土中钢筋通常是均匀锈蚀和点蚀同时发生，直接定量描述困难，所以采用名义均匀截面损失率和锈蚀率描述其锈蚀程度，锈蚀后采用名义屈服强度和名义极限屈服强度表征钢筋强度和锈蚀量的关系。锈蚀后钢筋的实际屈服强度fys=ky′fy0；实际极限强度fus=ku′fu0，式中fy0和fu0分别为未锈蚀钢筋的屈服强度和极限强度；ky′和ku′分别为名义屈服强度相对值和名义极限强度相对值，其取值标准参照沈德建模型［24］确定。

1.4 混凝土强度变化模型

混凝土强度在海洋环境下受腐蚀降低是结构劣化的重要表现之一，其随时间的变化规律也是建立混凝土结构抗力随机过程模型的关键。初期混凝土强度随着水泥水化作用的进行而增大，而混凝土强度下降的过程是十分缓慢的，混凝土强度的标准差随时间的推移而缓慢增大。

牛荻涛［25］总结分析了国内外混凝土暴露试验和结构实测数据，统计回归出了海洋环境下混凝土强度平均值和标准差的时变模型

式中：μfcu（t）为28 d混凝土立方体抗压强度均值；σfcu（t）为28 d混凝土立方体抗压标准差；μfcu（t）为服役期第t年混凝土立方体抗压强度均值；cuσf（t）为服役第t年混凝土立方体抗压强度标准差。

1.5 锈蚀钢筋混凝土构件粘结性能退化规律

钢筋锈蚀造成结构劣化的重要表现之一是钢筋与混凝土之间粘结性能的减弱，常通过引入钢筋与混凝土协同工作系数来描述由于粘结性能减弱引起承载力降低的过程。但是协同工作系数在现有的锈蚀后构件承载力计算模型中实质上是对钢筋强度的折减，没有明确钢筋有可能达不到屈服强度；协同工作系数在一定程度上反映了构件锈蚀后共同承载的能力，但是忽略了由于构件参数不同，即使在一样的锈蚀情况下，粘结性能减弱导致的钢筋与混凝土共同承载能力的变化幅度不同。以物理意义更为明确的钢筋利用系数来表征由于粘结性能减弱引起的承载力降低更为合理。受拉钢筋利用系数αS的计算公式参见耐久性评定意见［26］。

2 耐久性可靠度分析方法

由海洋环境下钢筋混凝土结构劣化的机理，可将海洋环境下结构耐久性寿命分为钢筋初始锈蚀、混凝土保护层开裂、钢筋混凝土表面出现最大外观损伤三个阶段。通过前文中的结构劣化随机过程模型，可以得到各个阶段的极限状态方程，并建立相应的概率模型，利用误差传递原理推求随机过程模型统计参数，并利用JC法计算其使用周期某确定时刻的可靠度指标，得到其动态可靠度指标变化曲线，和预定的可靠度值相比较，来分析确定各个阶段的寿命。根据统一标准要求［27］，结构构件正常使用极限状态的可靠指标，根据其可逆程度取为0～1.5。

2.1 钢筋初始锈蚀时间

海洋环境下，钢筋锈蚀主要由氯离子侵蚀引起，并且由于混凝土保护层都较厚，碳化并不是主要影响因素，所以钢筋初始锈蚀的极限状态方程

式中：Ccr为钢筋表面临界浓度（%，占混凝土重量百分比），为随机变量；C（c，t）为t时刻钢筋表面氯离子浓度（%，占混凝土质量百分比）；c为混凝土保护层厚度，mm。

认为随机变量Ccr服从正态分布，随机过程C（c，t）转化为确定时刻的随机变量，认为其服从正态分布，由误差传递原理可以求得Ccr和C（c，t）的统计参数，采用JC法计算钢筋开始锈蚀的可靠度指标，与目标可靠度指标比较来确定时间。钢筋开始锈蚀目标可靠度指标按照混凝土碳化引起的钢筋开始锈蚀目标可靠指标［27］取为 0.5。

2.2 混凝土保护层开裂时间

钢筋锈蚀深度模型是通过大量的实验统计数据，着眼于主要影响因素，建立简单的方便工程应用的模型，选取锈蚀深度模型作为混凝土保护层开裂模型。当混凝土结构锈胀开裂的极限状态方程可以表示为

式中：δcr混凝土保护层锈胀开裂时钢筋的锈蚀深度，mm；δ（t）为锈胀开裂前钢筋锈蚀深度随时间的发展过程，mm；t为以保护层初始开裂时为起点单位为，a。

锈胀开裂模型选择耐久性评定标准模型［23］，所以由规范和式（9）即可得出δcr和δ（t）模型。根据文献［28］随机变量δcr服从对数正态分布，随机过程δ（t）转化为确定时刻的随机变量，认为其服从正态分布，由误差传递原理计算δcr和δ（t）的统计参数，以式（11）为功能函数，采用JC法计算保护层开裂的可靠度指标，与目标可靠度指标比较来确定开裂时间。其目标可靠度指标根据统一标准要求范围［27］，基于使用评估准则，取为1.0。

2.3 钢筋混凝土表面出现最大外观损伤时间

正常使用极限状态下，结构的耐久性寿命是混凝土表面的裂缝宽度超过规定的限值，其极限状态方程可以表示为

式中：δd为混凝土表面裂缝达到限定最大值时的锈蚀深度，mm；δ′（t）为钢筋混凝土表面裂缝达到限定最大值之前的锈蚀深度，mm；t为时间，单位为a，从保护层开裂开始算起。

根据文献［28］随机变量δd服从对数正态分布，随机过程δ′（t）转化为确定时刻的随机变量，认为其服从对数正态分布，由误差传递原理计算δd和δ′（t）的统计参数，以式（12）为功能函数，采用JC法计算表面出现最大外观损伤的可靠度指标，与目标可靠度指标比较来确定出现最大损伤的时间。其目标可靠度指标根据统一标准要求范围［27］，基于使用评估准则取为1.0。

3 承载力可靠度分析方法

在设计使用期T年内结构的失效概率可表示为Pf（T）=P｛Z（t）=R（t）-S（t）＜0，t∈［0，T］｝，式中R（t）和S（t）分别为结构抗力和荷载作用效应随机过程，直接由上式通过复杂的积分求出结构的失效概率比较难。将设计使用基准期T等分为N个时间段，结构和抗力离散为N个时间段上的随机变量，则上式变成求串联体系的可靠度问题，并假设每个时间段上结构抗力和荷载的随机变量服从某种分布形式，于是就可得到某种形式的极限状态的功能函数，便可采用JC法求解其可靠度，并与目标可靠度指标比较求得结构的承载力使用寿命。根据文献［1］承载力极限状态的目标可靠度指标可根据建筑物安全级别和破坏形式确定，当破坏形式是延性破坏时，可取为3.5；破坏形式是脆性破坏时，取为4.0。

3.1 荷载

结构在服役过程中承受着各种形式的荷载，各部门颁布的可靠度设计统一标准，采用的是校准法，只考虑永久荷载和可变荷载作用，如果考虑多种可变荷载效应，则通过可变荷载的概率组合的方式。只考虑永久荷载效应和一种可变荷载效应组合如下

式中：Q（t）为可变荷载作用；G为恒载作用；CQ、CG分别为可变作用和永久作用的作用效应系数。

3.1.1 永久荷载作用效应

结构的恒载效应（如自重）不随时间变化，一般视为服从正态分布的随机变量［1］。其概率分布函数

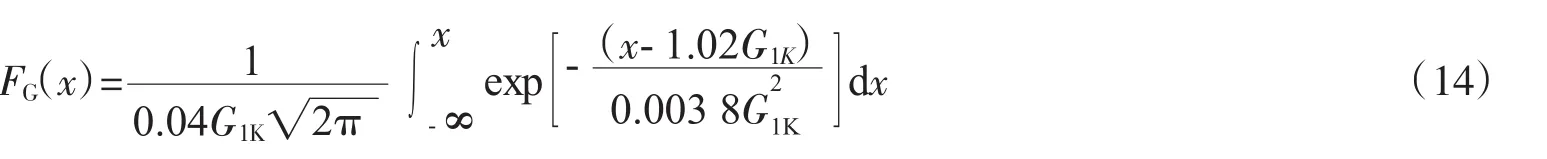
式中：G1K为恒载设计值；永久荷载的均值μG=1.02G1K，标准差σG=0.04G1K。

3.1.2 可变荷载

可变荷载作用效应QT随时间变化，是随机过程，将设计基准期等分为N个时间段，每个时间段为τ=T/N，每个时间段的最大可变荷载为Qτ，其分布函数为Fτ（x），假设各个时间段Qτ相互独立，则QT分布为

认为可变荷载Qτ服从极值I型分布

则设计基准期，随机变量QT也服从极值I型概率分布，其概率分布函数中的参数为μT=μτ+lnN/α；αT=ατ。

3.2 结构抗力

现行的可靠度设计统一标准都将结构抗力视为不随时间变化的，但是实际上结构构件在整个服役期内受到环境侵蚀以及外部荷载作用等影响，是逐渐随时间降低的过程。将1节所述的结构劣化的随机过程代入到规范中所述的结构构件抗力计算公式当中，就得到了结构抗力的随机过程模型，高桩码头结构构件的抗力计算模型参考王军［13］的研究。与可变荷载随机过程的处理方式相似，将结构抗力在设计基准期T年内，也等分为N个相等时段，取每个时间段抗力的均值Rτ，并假设其服从某种分布。

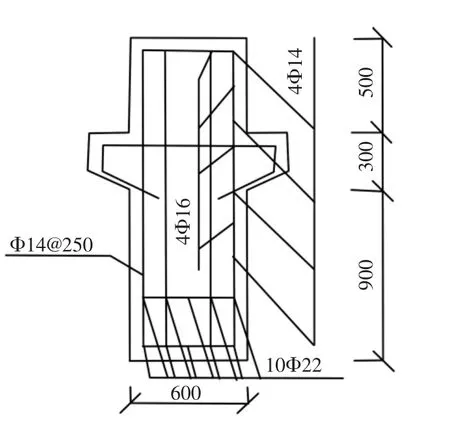
图1 横梁配筋截面Fig.1 Reinforced drawing of beam

4 工程算例

4.1 结构系统的主要参数

某钢筋混凝土高桩梁板结构码头，码头前沿水深为-14.0 m，码头顶面高程为4.5 m，码头结构由前桩台，后桩台和接岸结构组成，排架间距7 m。

面板：采用空心板，6 340 mm×4 460 mm×500 mm，圆形开孔直径300 mm，共8个孔，在横梁上的搁置宽度180 mm，纵梁上的搁置宽度30 mm，板断面情况；面板采用C35混凝土，水灰比0.45，主筋保护层厚度60 mm，底层配有26Φ22二级钢筋，顶层配有10Φ14二级钢筋，全板配6Φ6的I级箍筋，箍筋间距300 mm。

横梁：为混凝土叠合梁，面板以下部分为预制混凝土T型梁，其上部与面板连接部分为横梁的现浇叠合部分，结构断面特性见图1；横梁采用C35混凝土，水灰比0.45，主筋保护层厚度64 mm；底部配10Φ22的II级纵向受拉钢筋，上部配2Φ14@250的水平分布筋，10Φ16的短筋，竖向分布筋4Φ14@250。

基桩：650 mm×650 mm的预应力混凝土空心方桩，空心直径D=350 mm，采用C40混凝土，水灰比为0.40护层厚度60 mm。

该高桩码头的使用荷载主要为堆货荷载。

码头的面板处于大气区及浪溅区（但纵向受力钢筋处于浪溅区，所以面板按浪溅区考虑）；横梁处于浪溅区；基桩处于水位变动区和水下区。

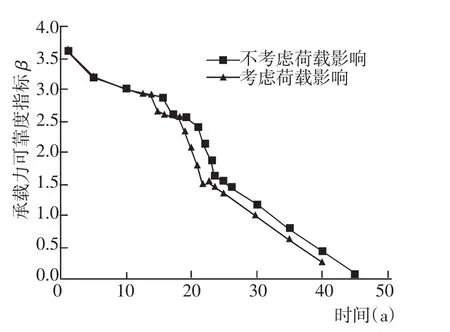
图2 荷载水平对面板承载力寿命影响（0.5倍荷载）Fig.2 Effect of loading lever on concrete face

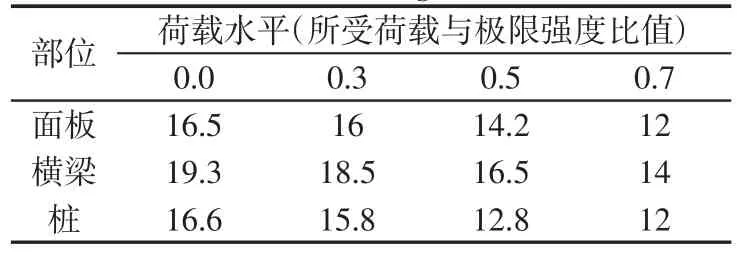
表6 荷载水平对钢筋开始锈蚀寿命影响Tab.6 Effect on initial corrosion of rebar under loading lever a

4.2 结构耐久性可靠度与承载力可靠度计算分析结果

采用2节和3节所述方法，计算码头面板、横梁以及桩的可靠度，并分析荷载水平对其耐久性寿命和承载力寿命影响。结果表明荷载水平对于耐久性寿命影响十分明显，对承载力寿命有一定的影响，表6是荷载水平对钢筋开始锈蚀寿命的影响，目标可靠度指标为0.5，图2为是否考虑荷载水平对面板承载力可靠度动态指标的影响（荷载水平为0.5倍荷载）。

5 结语

详细探讨了海洋环境下受荷载作用的结构物的劣化过程，以其为基础，建立了考虑荷载作用下抗力时变特性的钢筋混凝土结构的耐久性寿命和承载力寿命的分析方法，并以具体算例加以说明，对沿海钢筋混凝土建筑物的耐久性寿命和承载力寿命分析方法做了很有意义的探讨。

［1］港口工程结构可靠度设计统一标准编制组.港口工程结构可靠度［M］.北京：人民交通出版社，1992.

［2］Francois R，Maso J C.Effect of damage in reinforced concrete on carbonation or chloride penetration［J］.Cement Concrete Research，1988，18：961.

［3］YOON S C，WANG K J.Interaction between Loading，Corrosion，and Serviceability of Reinforced Concrete［J］.ACI Materials Journal，2000，97（6）：637-644.

［4］LI C Q.Corrosion initiation of reinforcing steel in concrete under natural salt spray and service loading—Results and analysis［J］.ACI Materials.Journal.，1997（6）：690-697.

［5］水金锋.海潮影响区钢筋混凝土桥梁的耐久性研究［D］.大连：大连理工大学，2005：5-6.

［6］何世钦.氯离子环境下钢筋混凝土构件耐久性能试验研究［D］.大连：大连理工大学，2004.

［7］张德锋.现代预应力混凝土结构耐久性研究［D］.南京：东南大学，2001.

［8］王元战，田双珠，王军，等.不同环境条件下考虑荷载影响的氯离子扩散模型［J］.水道港口，2010，31（2）：125-131.WANG Y Z，TIAN S Z，WANG J，et al.Chloride diffusion model of RC member in various marine environments considering loading effect［J］.Journal of Waterway and Harbor，2010，31（2）：125-131.

［9］王元战，黄东旭，王军.考虑荷载影响的钢筋混凝土构件钢筋锈蚀模型［J］.水道港口，2011，32（3）：202-206.WANG Y Z，HUANG D X，WANG J.Reinforcing bar corrosion model of RC member considering load effect［J］.Journal of Waterway and Harbor，2011，32（3）：202-206.

［10］赵国藩.结构可靠性理论［M］.北京：中国建筑工业出版社，2000.

［11］牛荻涛.混凝土结构耐久性与寿命预测［M］.北京：科学出版社，2003.

［12］王元战，田双珠，黄长虹，等.考虑抗力时变特性的高桩码头结构全寿命可靠度分析［J］.港工技术，2011，10（48）：21-25.WANG Y Z，TIAN S Z，HUANG C H，et al.Analysis on Full Life Reliability of Piled Wharf While Considering Resistance Time-varying Characteristic［J］.Port Engineering Technology，2011，10（48）：21-25.

［13］王军.荷载作用下钢筋混凝土结构耐久性分析方法研究［D］.天津：天津大学，2008.

［14］Atkinson A，Hearne J A.Mechanistic model for the durability of concrete barriers exposed to sulfate-bearing groundwater［J］.Materials Research Society Symposium Proceedings，1990，176：149-156.

［15］Mangat P S，Molloybt.Prediction of long term chloride concentration in concrete［J］.Materials and structures，1994，27（7）：338-345.

［16］Costa A，Appleton J.Chloride penetration into concrete in marine environment-Part II：Prediction of long term chloride penetration［J］.Materials and Structures，1999，32（6）：354-359.

［17］Dimitri V.Factors Affecting Life-Cycle Cost Analysis of RC Structures in Chloride Contaminated Environments［J］.Journal of Infrastructure Systems，ASCE，2007，13（2）：135-143.

［18］施惠生，王琼.海工混凝土使用寿命预测研究［J］.建筑材料学报，2004，7（2）：161-167.SHI H S，WANG Q.Research on Service Life Prediction of Marine Concrete［J］.Journal of Building Materials，2004，7（2）：161-167.

［19］Stephen L A，Dwayne A J，Matthew A M，et al.Predicting the service life of concrete structures：an environmental methodology［J］.ACI Structural Journal，1998，95（2）：205-214.

［20］COSTA A，Appleton J.Chloride penetration into concrete in marine environment-Part I：Main parameters affecting chloride penetration［J］.Materials and Structures，1999，32：252-259.

［21］吴相豪，李丽.海港码头混凝土构件氯离子浓度预测模型［J］.上海海事大学学报，2006，27（1）：17-20.WU J H，LI L.Prediction model of chloride ion concentration at concrete element in harbor dock［J］.Journal of Shanghai Maritime University，2006，27（1）：17-20.

［22］LIU Y P.Modeling the Time-to-Corrosion Cracking of the Cover Concrete in Chloride Contaminated Reinforced Concrete Structures［D］.USA：the Virginia Polytechnic Institute and State University，1996.

［23］CECS 220：2007，钢筋混凝土结构耐久性评定标准［S］.

［24］沈德建，吴胜兴.海水浪溅下混凝土中锈蚀钢筋性能试验研究及仿真分析［J］.工业建筑，2005，35（3）：58-62.SHEN D J，WU J X.Experimental study and simulation analysis on corroded bars in concrete at the marine cycle［J］.Industrial Construction，2005，35（3）：58-62.

［25］牛荻涛.海洋环境下混凝土强度的经时变化模型［J］.西安建筑科技大学学报，1995，27（1）：49-52.NIU D T.Changing models of concrete strength along with time in marine environment［J］.Journal of Xi′an University of Architecture&Technology，1995，27（1）：49-52.

［26］GB 50068-2001，建筑结构可靠度设计统一标准［S］.

［27］牛荻涛.混凝土结构耐久性与寿命预测［M］.北京：科学出版社，2003.

［28］孙艺.海洋环境下高桩码头耐久性分析方法研究［D］.天津：天津大学，2005.