树木枝干点云数据的等值线提取

高士增，张怀清，刘 闽，何清平，罗立平

（1.中国林业科学研究院 资源信息研究所，北京 100091；2.湖南省攸县黄丰桥林场 广黄分场，湖南攸县 412306）

随着森林可视化和林业测绘技术的不断发展和深入，中国数字化森林的建设进程不断向前推进［1］。地面三维激光扫描作为一种新型的可以自动、连续、快速地获取目标物的三维点云数据的测绘技术，已在林业资源调查［2］、 林分结构研究［3］以及单木三维重建［4］等方面得到了初步应用［5］。与传统森林资源调查方法作业周期长、工作效率低、劳动强度大、数据单一相比，应用地面三维激光扫描技术获取测树因子速度更快、精度更高，而且不会对林木造成损害，有利于保护生态环境［6］。利用三维激光扫描的点云数据绘制树木枝干的等值线图，不仅可以对点云数据进行精简和压缩，得到的树木枝干等值线模型还可用于单木的三维重建和树木的形态结构研究，对于树木的可视化模拟具有非常重要的意义。传统的离散矢量点云数据的等值线提取方法可以分为规则数据场的等值线提取和不规则数据场的等值线提取［7－11］。对于树木枝干点云，不适合采用这些方法，因为对树木枝干点云数据进行表面建模，构建真三维的Delauney三角网的技术还不成熟。当点云数量过多时，构建的树木三角网格模型数据太大；而当点云数量过少时，构建的模型在细节上又不能令人满意。本研究首先根据树木的分枝特征将点云数据分割成不同的部分，并分析了点云的空间分布情况，然后将点云数据按照y坐标分层，对于树木各部分不同层次的点云利用迭代的凸包算法分别提取等值线。本方法解决的关键问题在于，针对由激光扫描得到的点云数据多、无拓扑信息、低采样间隔、高采样细节的特点，在未构建树木三维模型的前提下，直接提取树木枝干的等值线模型。

1 数据获取和分析

采用FARO Laser Scanner Photon地面三维激光扫描仪，在湖南省株洲市黄丰桥林场进行数据采集实验。扫描样木为落叶后的鹅掌楸Liriodendron chinensis。根据样木周边环境和样木自身特点，选取3个角度，设立3站对样木进行扫描。由于要建立样木精密的三维模型，每站首先采用了较低密度的采样精度扫描全局，然后使用较高密度的采样精度对样木所在的区域进行局部扫描。利用扫描软件配准不同站点的扫描数据。手动删除树木周围物体的扫描点，去除噪声点，分离出树木的点云数据。

在对每一层点云进行凸包计算时，需要对树木不同部位的枝干分别计算，因此，需要把树木枝干的点云数据分割成不同的部分。对此，在利用扫描软件导出点云数据时，首先通过坐标变换将点云数据的坐标原点设置为树木的根部，且树木的主干大致平行于y轴，然后依据树木的分枝特征，将树木不同部位的点云数据分别导出，编号后合并。

2 点云数据的等值线提取

2.1 提取等值线折线

采用凸包算法提取每层点云数据的等值线折线。每层数据中，假设同一编号枝干的点集P={P0，…，Pn-1}，n为点的数量，其凸包是一个最小的凸多边形Q，并且满足P中的所有点或者在Q上，或者在Q的内部。使用不同编号枝干上的点云可以构建不同的凸包，凸包的数量等于点云层中枝条的数量。凸包算法在计算机图形学、模式识别、图像处理等领域有着广泛的应用。常用的构建凸包的算法是Graham扫描法和Jarvis步进法。

当点集P有3个或3个以上的点时，凸包算法的过程如下：①计算点集最左边的点为凸包的顶点的起点，如图中的P0。②遍历P中其他所有点，计算有向向量P0Pi。③如果P中的其他点全部在向量P0Pi的同一侧，则Pi为凸包的下一个顶点，如图1。

此过程执行后，按照任意2点的顺序把点按极角自动顺时针或逆时针排序，而左侧或右侧的判断则可以用矢量点积性质来实现。

2.2 内部离散点的归类

利用凸包算法得到的凸多边形边界上的点是点集P的一个子集，可以认为P代表任一枝条在某一高度范围内的等值线的一个近似。在此高度范围内，树枝的表面仍有离散点没有包括在该折线上，利用该折线代表其等值线过于简单。因此，为了更加精确地表达等值线，需要进一步将这些离散点归类到当前的折线上。

如图2所示：QiQi+1是当前折线上连接凸包中相邻2点的一条线段，Pj为凸包内部尚未加入到折线上的一个离散点。对于点Pj，应该归类于其最近的折线线段，并且该点在线段的投影Pj0应该在线段上。连接 QiPj和 Qi+1Pj这2条线段，组成三角形QiQi+1Pj。

三角形QiQi+1Pj的2个内角α和β，依据平面几何的知识，可以得到以下的判别条件：假如α和β中有一个角度大于90°，那么投影点Pj0在线段QiQi+1外。假如α和β中有一个角度等于90°，那么投影点Pj0位于Qi或 Qi+1点上。假如α和β全部小于90°，那么投影点Pj0在QiQi+1内部。

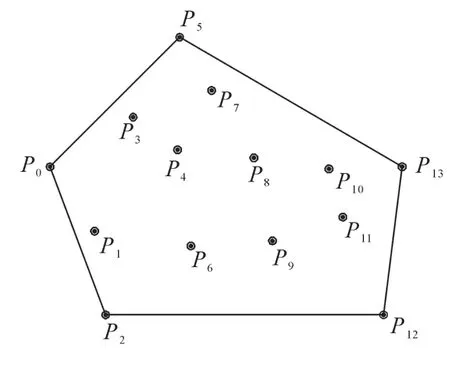
图1 凸包算法Figure 1 Convex hull algorithm

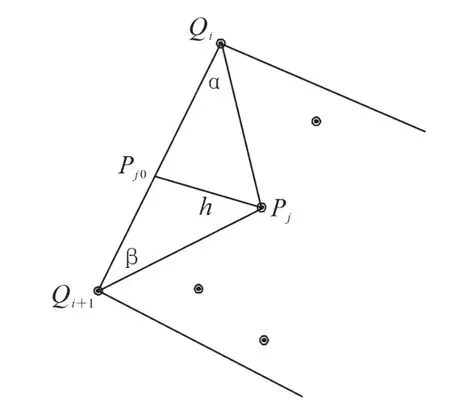
图2 离散点的归类Figure 2 Classify discrete points

对每个尚未归类的点Pj，计算该点到当前等值线各线段的投影点，利用上述方法判断投影点是否在其对应的线段上，然后利用该点到各线段的距离，对Pj归类。每个待定点只能归类于α和β均小于90°并且距离最近的线段。

采用上述方法对当前的等值线和待定点进行归类后，对于凸包折线的每条线段，重新计算其和归类到该线段的待定点的凸包，由此得到局部区域的凸包。然后将所有的局部凸包在原凸包折线的线段处断开，得到不闭合的折线段。按顺序将前后折线段进行连接，即得到下一级折线。该过程如图3所示。

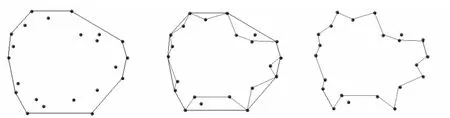
图3 迭代的凸包算法Figure 3 Iterative convex hull algorithm

整个算法的流程如图4所示。

运用此方法可以保证每次迭代完成后的相邻层之间的等值线不会产生边缘交叉的问题，可以满足等值线的基本特点。

第一次调用凸包算法得到的是一个凸多边形，对此凸多边形继续使用凸包算法得到的局部区域也是凸多边形，但是合并一系列的局部凸多边形之后得到的等值线却是凹多边形。对凹多边形再次进行剩余点的归类和调用凸包算法，得到的仍旧是凹多边形。除第一次调用凸包算法的到的是凸多边形，以后每次迭代后的合并结果都是凹多边形。调用凸包算法完成后，剩下的每个待定点和当前折线的拓扑关系是一致的，在折线的内部或者外部。可以知道，奇数次迭代之后的待定点都在折线的外部；偶数次迭代之后的待定点都在折线的内部。

3 研究实例

3.1 点云数据的空间分布

选取1株3年生的鹅掌楸，树高为 2.26 m。设全部点云为［Pi（xi，yi，zi），i＝0，…，n－1，n为点的总数］。坐标范围为（xmin，ymin，zmin）～（xmax，ymax，zmax）。按照坐标 y方向，且按照一定的高度范围，对数据进行分层，得出任意一点 Pi（xi，yi，zi）的层序号为：

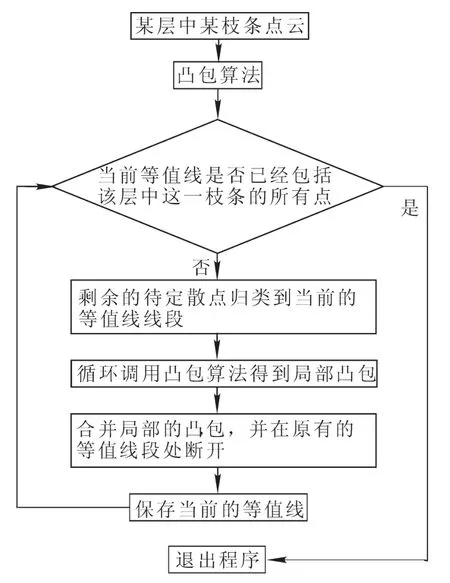
图4 算法流程图Figure 4 Algorithm flowchart

式（1）中：dz表示层的厚度，ki表示Pi点的层号。

分析合并后样木点云数据，其坐标范围结果如下：xmin=－0.364 9，xmax=0.322 7，ymin=0，ymax=2.259 4，zmin=－0.266 5，zmax=0.462 8。该批点云的总共点数为104 808个，根据扫描精度，取dz=2.5 mm，则计算可知总共分为904层，平均每层点云数量为116个，所有层的点云数量分布以及和枝条数量的关系如图5A所示。取y坐标为1.000 m（即取1.008 5≤y＜1.001 0）的层数据，该层总共点数为117个，其空间分布如图5B所示。

图5 点云的空间分布Figure 5 Spatial distribution of points cloud

由图5可以看出：使用地面激光扫描仪扫描的点云数据，沿树高方向每层的数据量都很大。每层点云的数量随枝条个数的增加有增大的趋势。并且从点的分布图中基本可以看出该层点云的等值线形状。

3.2 等值线模型的提取

使用集成开发工具Visual Studio.Net，运用C#语言结合多媒体编程接口DirectX，编程实现树木枝干等值线的提取。

点云数据分层后，每层数据中都至少包括一条枝干。当点云层的厚度较小时，可以认为此层中的点云具有同一高度值。图6A为提取的整棵树木的等值线图。图6B为当高度等于0.80 m（0.798 5≤y＜0.801 0）时相应的点云层，此层数据中共包括5个树木枝干，编号分别为①③④⑤⑥。对不同的枝干调用上述迭代的凸包算法，分别提取出其凸包折线，图6C为提取出的树木枝条编号为③的凸包折线。由图6可以看出在没有先验等值线知识和建立点云对象模型的条件下，利用迭代的凸包算法可以有效的对离散点数据进行连接，形成点云的等值线模型。

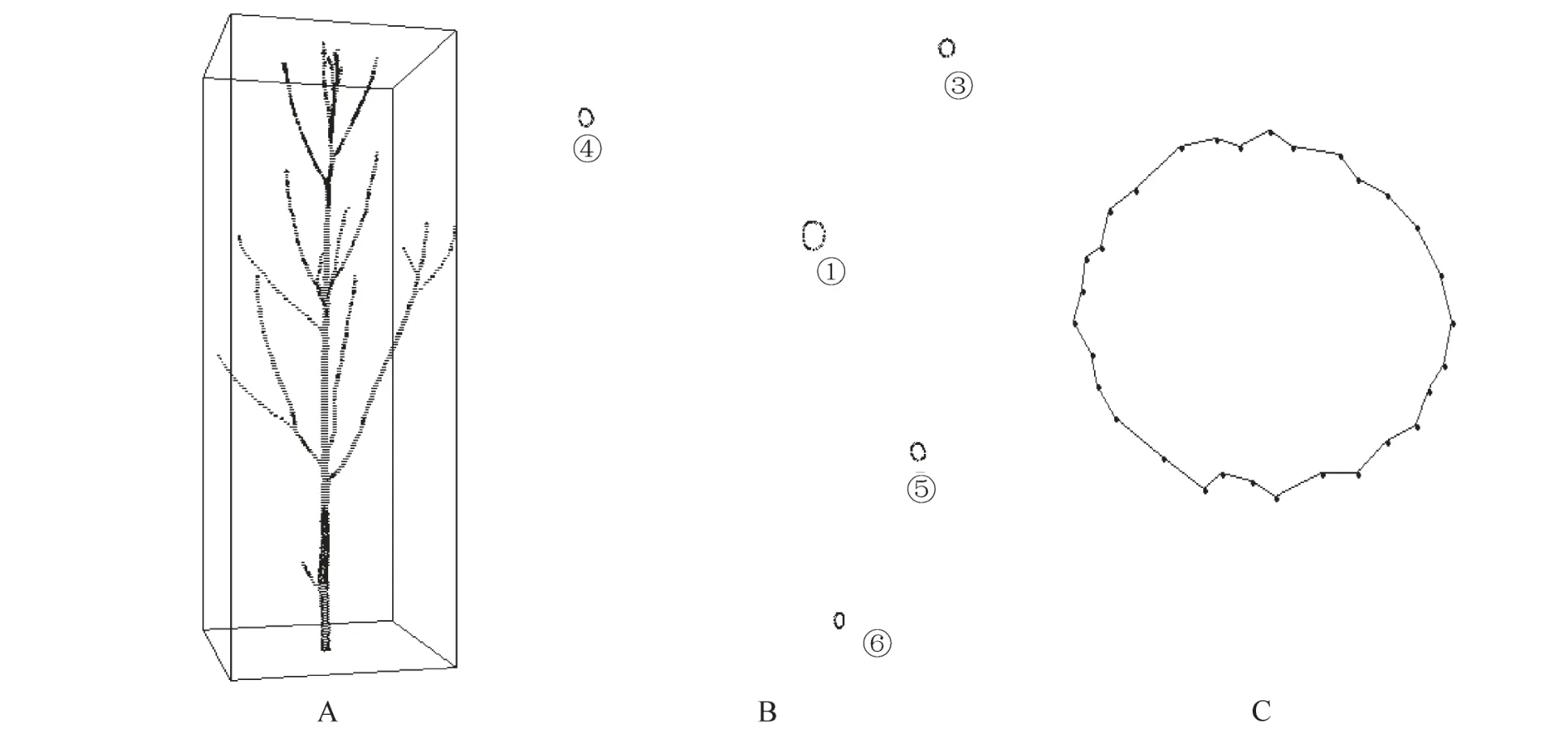
图6 等值线模型实例Figure 6 Contour model instance

3.3 等值线精度验证

利用提取出的凸包折线的长度计算不同高度树木枝干的直径，与实际测量树木枝干的直径相对比验证等值线的精度。其中，因树干方向大致和凸包折线所在的平面垂直，凸包折线的长度可以当作树干的圆周长，以此计算树干直径。但是，枝条的方向和凸包折线所在的平面有一定的夹角，矫正后才可用来计算枝条的直径。矫正过程如图7所示。

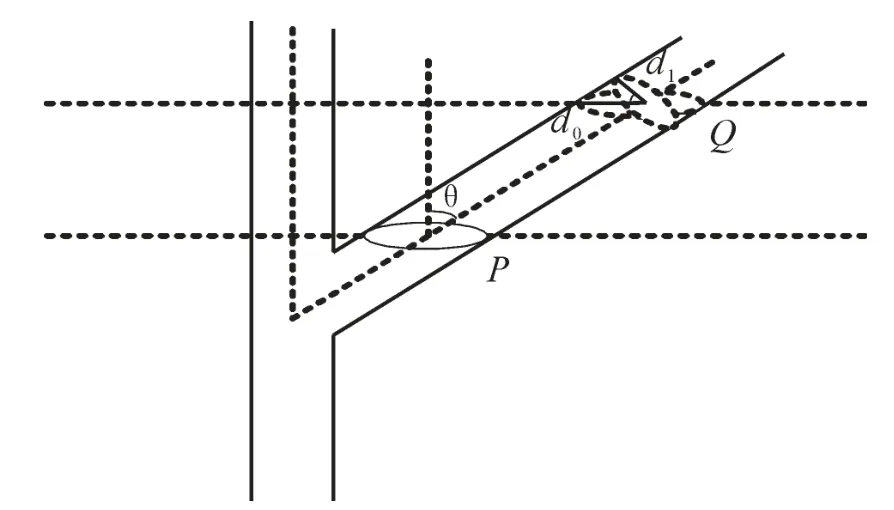
图7 直径矫正图Figure 7 Diameter correction

图7中：P为枝条最低端的凸包折线，Q为待矫正凸包折线，以凸包折线中距离最远的2点的中点为凸包折线的中心，连接PQ的中心与树干方向的夹角为θ，d0为矫正前枝条的半径，d1为矫正后枝条的半径，由式（2）可求出 d1。

利用上述方法可以提取出树木不同高度枝干的直径，部分数据和实际测量数据对比如表1所示。其中，通过等值线模型计算出的数据记为扫描数据，编号1～15为不同高度树干直径，编号16～30为矫正后的样木不同部位的枝条直径。

由表1可以看出：扫描数据比实测数据整体偏大，主要原因是绝大多数凸包折线的长度大于树木枝干实际的圆周长，因此，计算得出的直径会偏大。以扫描数据为自变量x，实际测量的数据为因变量y，做出样木枝干直径的散点图，并进行线性回归拟合，得到回归方程。由图8中的回归方程可以看出：R2达到0.996 4，置信度为95%，说明计算数据和实测数据紧密相关。

图8 直径散点图Figure 8 Scatter diagram of diameter

表1 扫描数据和测量数据对比Table 1 Comparison of scan data and actual data

利用扫描数据，通过回归方程计算直径的理论值，根据公式（理论值－实测值）/实测值，得到误差为3.4%，误差数值满足林业测树的要求，说明利用此种方法提取的等值线模型可以用于树木枝干任何高度处的直径的测量。

4 结语

针对利用地面三维激光扫描技术得到的树木枝干点云数据建模困难的问题，提出了采用分层提取等值线的方法建立树木枝干的等值线模型，所建立的模型包含树木枝干的原始信息，可以用于树木基本测树因子的测量。

使用凸包算法提取每层点云中树木不同枝干的等值线，然后将剩余的离散点归类到当前的等值线线段，迭代掉用凸包算法，得到该层的等值线模型。此方法不仅算法简单，而且提取的等值线不存在边缘交叉问题，提取的等值线的精度可以满足林业测树的要求。

应该指出的是，使用此方法提取树木枝干的等值线对原始数据的要求很高，点云采样密度不能过大，而且必须严格去噪。如何在此等值线模型的基础上构建树木枝干的Delauney网格结构将是今后进一步研究的重要内容。

［1］赵阳，余新晓，信忠保，等.地面三维激光扫描技术在林业中的应用与展望［J］.世界林业研究，2010，23（4）：41－45.ZHAO Yang，YU Xinxiao，XIN Zhongbao，et al.Application and outlook of terrestrial 3D laser scanning technology in forestry［J］.World For Res，2010，23（4）∶41－45.

［2］JAKOB W.Application and statistical analysis of terrestrial laser scanning and forest growth simulations to determine selected characteristics of Douglas-fir stands［J］.Folia For Polon Ser A，2009，51（2）∶123－137.

［3］GABOR B，GEZA K.Algorithms for stem mapping by means of terrestrial laser scanning［J］.Acta Silv Lign Hung，2009，5（1）∶119－130.

［4］TANSEY K,SELMES N.Estimating tree and stand variables in a corsican pine woodland from terrestrial laser scanner data［J］.Int J Rem Sens，2009，30（19）∶5195－5209.

［5］宋宏.地面三维激光扫描测量技术及其应用分析［J］.测绘技术装备，2008，10（2）：40－43.SONG Hong.Analysis and utilization of terrain 3D laser scanning survey technique［J］.Geom Technol Equ，2008，10（2）∶40－43.

［6］王剑，周国民.基于激光扫描仪的树干三维重建方法研究［J］.微计算机信息，2009，25（8－3）：228－230 WANG Jian，ZHOU Guomin.3D Reconstruction of tree stems based on laser scanning of standing［J］.Microcomput Info，2009，25（8－3）：228－230.

［7］蒋瑜，杜斌，卢军，等.基于Delaunay三角网的等值线绘制算法［J］.计算机应用研究，2010，27（1）：101－103.JIANG Yu，DU Bin，LU Jun，et al.Algorithm of drawing isoline based on Delaunay triangle net［J］.Appl Res Comput，2010，27（1）∶101－103.

［8］LORENSEN W，CLINE H.Marching cubes∶A high resolution 3D surface construction algorithm［J］.Computer Graph，1987，21（4）∶163－169.

［9］吴杭彬，刘春.激光扫描数据的等值线分层提取和多细节表达［J］.同济大学学报，2009，37（2）：267－271.WU Hangbin，LIU Chun.Point cloud-based stratified contour extraction and its multi-lod expression with ground laser range scanning［J］.J Tongji Univ，2009，37（2）∶267－271.

［10］赵夫来，郝向阳.根据地性线绘制等高线的研究［J］.测绘学报，1999，28（4）：345－349.ZHAO Fulai，HAO Xiangyang.A research on contour plotting based on bone lines［J］.Acta Geod Cartograph Sin，1999，28（4）∶345－349.

［11］龚有亮，何玉华，付予傲，等.一种实用的等高线内插算法［J］.测绘学院学报，2002（3）：36－39.GONG Youliang，HE Yuhua，FU Yu’ao，et al.A practical contour interpolation algorithm［J］.J Inst Survey Map，2002（3）∶36－39.