超导-介质型Fibonacci光子晶体的透射谱与滤波特性分析
刘晚果,潘风明
(南京航空航天大学应用物理系,江苏南京 211100)
1 引 言
在现代光纤通信系统中,波分复用技术是实现信息高速、大容量传输的最佳方式。作为波分复用技术的核心部件,可调谐光滤波器的设计在其应用中占有重要地位。目前得以广泛应用的可调谐光滤波器大多基于Fabry-Perot干涉仪原理,利用光的干涉相长或相消来实现滤波的效果。现在可调谐光滤波器大多由干涉腔长度决定半高宽和调谐范围,通过驱动悬浮的高反射膜运动进行调谐。虽然其在精度和成本等方面有着较大的相对优势,但由于微机械器件的特点,悬浮膜表面与标准样板之间的偏差不得超过1/50~1/20个波长,其制备工艺精密而又复杂,且驱动电压增大会限制其运动范围。再者,由于其透射峰半高宽与调谐范围均与干涉腔长度成反比,调谐范围越大则半高宽也越大,二者不可兼得,这在一定程度上影响了滤波器性能的提高。考虑到现有可调谐光滤波器在尺寸调节上的诸多不便,对固定几何参数的滤波器设计方案的探索具有非常重要的意义。
近年来,基于光子晶体(Photonic Crystal)的滤波器研究报道层出不穷。光子晶体的概念最早由 S.John[1]和 E.Yablonovitch[2]于 1987 年分别独立提出,是一类介电常数在空间上呈周期分布多层人工电磁介质。由于它在光学和光电子领域有广泛的应用前景,其性质于近十几年来得到广泛的研究[3-5]。与处于晶体周期势场中的电子类似,在光子晶体中会形成电磁禁带,也称光子带隙,频率处于禁带的电磁波不能在光子晶体中传播。另一方面,对于准周期结构的Fibonacci光子晶体,其相关领域的研究也在迅速开展[6-8]。Fibonacci光子晶体的准周期结构基于Fibonacci迭代序列,其结构递推关系为 Sj=Sj-1Sj-2,S0=B,S1=A。该结构的透射谱呈现出准周期性,在光学定位领域有着广泛的应用,且结构对于不同频率的电磁波具有选择透过性,亦可实现滤波的效果[9]。若光子晶体中存在某种形式的缺陷,则光子带隙将发生结构上的变化,在原来光子带隙中出现缺陷带。文献[10]中提出了一种利用真空耦合层调节缺陷,实现光子晶体可调谐滤波性质的方法,其结构表示为(H1L1)15LC(H2L2)n,其中真空耦合层以及覆盖层可视为光子晶体的缺陷,通过调节耦合层LC的厚度实现对电磁波的透射率控制,得到了1.46~1.61 μm 的调谐范围,半高宽在2 nm以下。此结构虽然解决了驱动电压对滤波器性能的影响,但其对缺陷结构的控制也依赖于耦合层尺寸的变化。
带有金属层及超导层结构的光子晶体是最近讨论较多的课题[11-16]。文献[14]中提出了一种介质-金属的一维光子晶体结构,较传统光子晶体而言可有效减少介质对电磁波的吸收,增大透射率。文献[15-16]讨论了温度对超导结构光子晶体能带的影响。由于超导体的介电常数受到温度的影响,光子带隙会随温度变化,透射率亦会随光子带隙的变化发生相应的改变。考虑到超导体折射率随温度的变化相当敏感,这使得脱离微机械技术的温控可调谐光滤波器的设计成为可能。本文将光子晶体中的一种介质以超导材料取而代之,基于超导理论,利用传输矩阵法对超导-介质型Fibonacci光子晶体的透射谱进行计算,并分析各种几何与物理参数对透射峰位置及半高宽的影响。最后,在透射谱分析的基础上加入覆盖层,讨论结构的滤波特性,提出一种通过调节温度实现可调谐光滤波的理论新模型。
2 理论模型与计算方法
图1给出了 Fibonacci光子晶体S5的原理图。其中介质层B的折射率nB=保持不变。根据超导理论,超导层 A的介电常数 εrA可表示为[12]

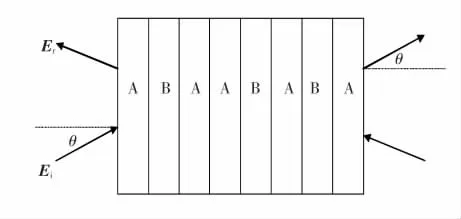
图1 带有超导层的一维Fibonacci光子晶体的原理图。其中A代表超导层,B代表介质层,Fibonacci等级j=5,θ为入射角,Ei,Er分别代表沿正向与负向传播的两个线性独立本征模式波。Fig.1 Schematic diagram of 1D Fibonacci photonic crystal with superconductor layer.A represents superconductor layer while B represents medium layer.Fibonacci level j=5.θ is incident angle.Ei,Er represent the two linear independent eigenmodes of waves propagating along the positive and negative directions separately.

其中Tc为超导临界温度,λL(0)为T=0 K时的London穿透深度e分别为电子的有效质量、0 K时的电子浓度与电子的有效电荷。
任意层n的电矢量均可表示为沿正向与负向传播的两本征模式波的线性叠加:

根据电磁场的边界条件可得到下列关系:

为了降低传输矩阵法的计算代价,在计算过程中尽量保证矩阵的稀疏性是必要的。因此在这里不打算直接运用传统意义上的传输矩阵,而作如下正交变换:

作此变换是为了保证透射系数计算式在不同本征模式选取下保持不变,并同时将传输矩阵对角化。在该变换下,式(4)变为

TAB与TBA分别反映了电磁波从B到A与从A到B传播过程中电矢量的变化。同样我们可以推导出在A层中的传输矩阵如下:

根据Fibonacci光子晶体的结构递推式,可给出全空间传输矩阵Mj的递推式

我们导出的全空间传输矩阵与文献[9]中的形式稍有不同。这是因为,若Fibonacci等级j为偶数,则最后一个B与A之间的分界面不存在,需要去掉最左端的矩阵TAB(即左乘其逆矩阵TBA)以作修正。
在得到全空间传输矩阵Mj后,其透射系数Tj可依照下式计算

其中‖Mj‖F代表矩阵的Frobenius范数,透射率Γj=可以看出式(5)的变换保证了Frobenius范数的保范性,因而对任意本征模式的叠加,式(11)均适用。
3 结果与讨论
作为一个例子,我们在正入射情况下,将超导层材料选作钇钡铜氧(YBCO),对其透射谱及滤波特性进行讨论。YBCO的超导临界温度Tc=93 K,0 K时的 London穿透深度 λL(0)=150 nm。其不同参数下的透射谱分别描绘于图2~6中。

图2 带有超导层的一维Fibonacci光子晶体在不同Fibonacci等级 j下的透射谱。j=7,9,11,13。dA=10 nm,dB=40 nm,nB=3,T=30 K。Fig.2 The transmission spectra of 1D Fibonacci photonic crystalwith superconductor layer at different Fibonacci levels j.j=7,9,11,13.dA=10 nm,dB=40 nm,nB=3,T=30 K.
图2给出了光子晶体在不同Fibonacci等级下的透射谱,dA=10 nm,dB=40 nm,nB=3,T=30 K。从图中可看出Fibonacci光子晶体较为明显的准周期性。在同一Fibonacci等级下,透射峰强度大多相等,而透射峰出现的周期却时长时短,因而各个透射峰的半高宽不尽相同,相比之下,第一透射峰半高宽最小。此外,Fibonacci等级对于透射峰半高宽有非常大的影响,随着Fibonacci等级的增加,透射峰越尖锐,半高宽越窄,其滤波特性也就越好。对于较高的Fibonacci等级,可以更加明显地看出在光子晶体中传播的电磁波存在一个截止频率。而事实上,超导体本身存在着一个频率禁带。根据式(1),当超导层的介电常数为0时(理想导体),电磁波不能在其中传播,超导截止频率fc可表示为

可以计算出T=30 K时YBCO的截止频率fc=320 THz,小于fc的即是超导的频率禁带。但由于光子晶体结构中介质的存在,使得实际截止频率受光子带隙的影响,在原超导频率禁带处出现通带,导致实际截止频率f'c远比fc要小。当j=11时,第一透射峰位于 f=69.26 THz≈f'c< fc,半高宽,能得到较理想的透射峰。因此以下的讨论均针对S11(144层)。我们将S11在不同介质层厚度与介质层折射率下的透射谱分别描绘于图3与图4中。

图3 带有超导层的一维Fibonacci光子晶体在不同介质层折射率 nB 下的透射谱。nB=2,3,4,5,dA=10 nm,dB=40 nm,T=30 K,j=11。Fig.3 The transmission spectra of 1D Fibonacci photonic crystal with superconductor layer at different refractive indices of ordinary medium layer nB.nB=2,3,4,5,dA=10 nm,dB=40 nm,T=30 K,j=11.

图4 带有超导层的一维Fibonacci光子晶体在不同介质层厚度 dB下的透射谱。dB=30,40,50,60 nm,dA=10 nm,nB=2,T=30 K,j=11。Fig.4 The transmission spectra of 1D Fibonacci photonic crystal with superconductor layer at different thicknesses of medium layer dB.dB=30,40,50,60 nm,dA=10 nm,nB=2,T=30 K,j=11.
从图3与图4中可以看出,增大介质层折射率与介质层厚度均能使透射峰向长波方向移动,截止频率降低。因为折射率的变化与厚度的变化对光学厚度的影响是等效的,可以认为介质层的光学厚度增加,透射峰向长波方向移动。还可进一步看出,当介质层的厚度或是折射率增大到一定程度的时候会出现第一透射峰透射率减小的现象,这与介质对电磁波的吸收有关。为了获得较好的滤波特性,透射峰半高宽与透射率需要同时兼顾。由于第一透射峰具有最小的半高宽,将其作为通频带是合适的,因而必须保证其透射率。
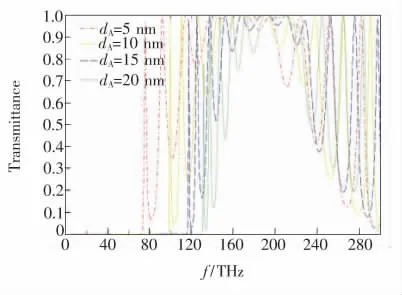
图5 带有超导层的一维Fibonacci光子晶体在不同超导层厚度 dA下的透射谱。dA=5,10,15,20 nm。dB=40 nm,nB=2,T=30 K,j=11。Fig.5 The transmission spectra of 1D Fibonacci photonic crystal with superconductor layer at different thicknesses of superconductor layer dA.dA=5,10,15,20 nm.dB=40 nm,nB=2,T=30 K,j=11.
图5给出了不同超导层厚度下的透射谱曲线,可以看出超导层厚度减小,透射峰向长波方向移动,亦可推知超导层光学厚度的减小会导致透射峰向长波方向移动,且超导层厚度对于透射率的影响程度不及介质层厚度。结合图4与图5的结论,若定义厚度比ρ,则当ρ0时,整个结→构近似普通电介质,截止频率fc'→0,禁带消失;当ρ→∞时,整个结构近似为超导体,则截止频率fc'≈fc与(12)式给出的一致。通过调节厚度比可以使截止频率fc'在0到fc之间任意变化,从而调整第一透射峰的位置。
从图3~5还可以看出,较改变介质层光学厚度而言,改变超导层光学厚度使透射谱变化更为显著,且介质层和超导层厚度的变化也会影响到第一透射峰的透射率。可以看出,当dA=10 nm,dB=40 nm,nB=2时,第一透射峰的透射率几乎等于1,明显优于其它参数。由于温度可以通过改变超导层折射率来改变光学厚度达到与改变厚度等效的影响,超导层的折射率也比介质层要低,所以较介质层折射率而言其对透射率的影响并不是很大,而且温度的调节比几何参数的调节容易得多。从透射谱得到的这些结论都说明在滤波器设计中将温度作为调节透射峰位置的参数是合理的,亦即温控调谐是可以实现的。

图6 带有超导层的一维Fibonacci光子晶体在不同温度T 下的透射谱。T=22,44,66,88 K.dA=10 nm,dB=40 nm,nB=2,j=11。Fig.6 The transmission spectra of 1D Fibonacci photonic crystal with superconductor layer at different temperatures T.T=22,44,66,88 K.dA=10 nm,dB=40 nm,nB=2,j=11.
图6给出了温度 T=22,44,66,88 K 时的透射谱曲线。可以看出当T=22 K时透射率偏小,而T=88 K时半高宽太大,在后面讨论滤波特性时,这个问题可通过限制调节温度范围来解决。随着温度的升高,透射峰向长波方向移动。特别是当温度接近超导临界温度时,透射峰随温度的变化非常敏感。这也表明光子带隙可以通过温度进行调节。由于透射峰随温度变化的灵敏度较高,所以据此可设计新型的温控调谐滤波器。
有了对透射谱的讨论作为基础,我们可以讨论加上覆盖层后光子晶体的滤波特性。覆盖层的作用是将第一透射峰之外的其余透射峰屏蔽。经过测试,我们将结构选为S11(S5)n,其中(S5)n为覆盖层,指数n代表周期数,一个周期的结构为CACCACAC,与图1的不同是超导层与介质层互换。其中 C为不同于 B的另一种介质,nC=3.95,覆盖层 dA=9.5nm,dC=40 nm,该参数的选择依据是保证在光子晶体第一透射峰的频率处的电磁波于覆盖层有接近1的透射率,而在其它频率处则透射率急剧减小。在此覆盖层参数下,保持S11参数不变,不同周期覆盖层下的滤波特性已描绘于图7中。
从图7可以看出,较图6而言,加入覆盖层后保留了T=22,44,66 K时的第一透射峰,3个温度在15周期覆盖层下的透射率分别为0.872 7、0.983 4、0.958 5,在60 周期覆盖层下的透射率分别为0.840 1、0.959 5、0.934 6,没有太大的影响。而其余的透射峰皆有不同程度的衰减,且覆盖层周期数越大衰减越厉害,大部分透射峰几乎完全消失。当覆盖层周期数n=60时,第一透射峰以外的相当一部分波段透射率几乎可以忽略不计。而T=88 K时的透射峰并不理想,这只需要在调谐范围确定的温度范围内去掉相关区域即可。
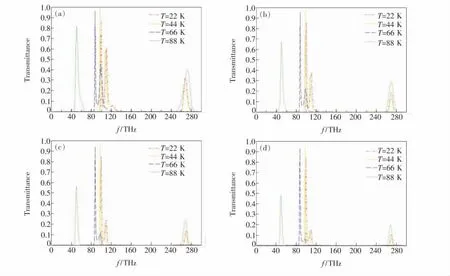
图7 不同周期覆盖层下S11(S5)n的滤波特性。nC=3.95,覆盖层dA=9.5nm,dC=40 nm,S11部分的参数与图6相同。(a)n=15;(b)n=30;(c)n=45;(d)n=60。Fig.7 The filter property of S11(S5)nat different periods of covering layer.nC=3.95,on the covering layer dA=9.5 nm,dC=40 nm,the parameters of S11are the same as Fig.6.(a)n=15.(b)n=30.(c)n=45.(d)n=60.
根据图7的结论,可推知在某个温度区间内必然存在一个连续的可调谐波段。为了便于观察,我们将覆盖层周期数n取为60,将透射率与频率以及相对温度(温度与超导临界温度的比值)的关系描绘于图8中。

图8 透射率随频率和相对温度的变化。覆盖层周期数n=60,其余参数均与图7相同。Fig.8 Dependence of transmittance on frequency and relative temperature.The periods of covering layer n=60.The other parameters are all same as Fig.7.
从图8可以定性地看出,每一个温度都唯一地对应着某个频率的透射峰,随着温度的升高,透射峰半高宽先减小,然后几乎保持不变,再往后略有增大;透射峰强度则是先有较大幅度的波动(在此过程中虽然透射率有时会高于0.9,但并不稳定),然后稳定在0.9以上,最后减小;透射峰处的频率随温度的变化始终是单调减少的,这从图6与图7中给出的4个温度下的半高宽也可以大致看出这个趋势。当T>0.824 8Tc时,透射率降至0.9 以下;当 T=0.824 8Tc=76.706 4 K 时,透射峰位于 75.94 THz 处,半高宽 0.162 THz,可作为可调谐频率的下限。当T<0.382 0Tc时,透射率不能稳定在0.9以上;当 T=0.382 0Tc=35.526 0 K时,透射峰位于 99.10 THz处,半高宽0.121 THz,可作为可调谐频率的上限。综上所述,若以透射率大于0.9为滤波器的技术指标,则当温度T在35.526 0~76.706 4 K 变化时,能得到99.10~75.94 THz的可调谐范围,其对应的波长范围为3.027 ~3.950 μm,较文献[10]中给出的可调谐范围要大,且在此波段内透射峰半高宽不会大于调谐范围边界处的半高宽(0.162 THz),始终被稳定控制在理想的范围内,兼顾了较窄的透射峰与较大的调谐范围。
由于采用了超导层结构,较之以传统的滤波器,该模型无需改变光学层的尺寸结构,而仅通过调节温度即可实现波段的调谐,与F-P结构的滤波器相比,省却了在平板上镀高反射膜的复杂工艺。而且,温控调谐的优点在于分离了半高宽与调谐范围的决定因素,即无需以牺牲调谐范围作为代价来使透射峰具有较小的半高宽。在参数选择合理的情况下,透射峰的半高宽将完全交予Fibonacci等级来决定,只要 Fibonacci等级足够高,就能得到理想的透射峰。调谐范围则可根据前文对透射谱的分析,通过选择合适的介质层或超导层材料、改变厚度比等参数来确定,与此同时,覆盖层的参数也会作相应变化。
4 结 论
基于应用于一般光子晶体计算的传输矩阵方法,根据超导理论,导出了一类新型结构—超导-介质型Fibonacci光子晶体的传输矩阵及透射系数的计算式。以超导层选作YBCO为例,计算得出了光子晶体的透射谱,并讨论了Fibonacci光子晶体结构对超导频率禁带的影响,以及介质层厚度、介质层折射率、超导层厚度、温度等参数对透射峰位置、透射率及半高宽的影响。在透射谱分析的基础上,给出了结构为可温控调谐的超导-介质型Fibonacci光子晶体滤波器的理论模型,分析了其滤波特性。这种结构的滤波器脱离了微机械技术,无需改变几何参数,仅需调节温度即可实现调谐,简化了制造工艺,且同时获得了较大的调谐范围与较小的半高宽,对新型可调谐光滤波器的设计有一定的借鉴意义。若将透射曲线改为反射曲线,本文的结果还可用于高反射镜的理论模型分析。
[1]John S.Strong localization of photonics in certain disordered lattices[J].Phys.Rev.Lett.,1987,58(23):2486-2489.
[2]Yablonovitch E.Inhibited spontaneous emission in solid state physics and electronics[J].Phys.Rev.Lett.,1987,58(20):2059-2061.
[3]Zhou P,You H Y,Wang S Y,et al.Effect of the inserted metal layer on the characteristic of light transmission of onedimensional photonic crystals[J].Acta Phys.Sinica(物理学报),2002,51(10):2776-2780(in Chinese).
[4]Qiu G X,Lin F L,Li Y P.Implementation of complete two-dimensional bandgap in photonic crystals of square Bravais lattice using complex unit cell[J].Acta Phys.Sinica(物理学报),2003,52(3):600-603(in Chinese).
[5]Liu N H,Fu J W.Effects of Kerr nonlinearity on the band-gap structure of one-dimensional photonic crystals[J].Acta Phys.Sinica(物理学报),2003,52(6):1418-1421(in Chinese).
[6]Liu X,Zhou J,Zhu B Q,et al.Electro-optical tunable filter with symmetric generalized Fibonacci photonic crystal[J].Acta Photon.Sinica(光子学报),2011,40(11):1723-1728(in English).
[7]Rostami A.Generalized Fibonacci quasi photonic crystals and generation of superimposed Bragg gratings for optical communication[J].Microelect.J.,2006,37(9):897-903.
[8]Mauriz P W,Vasconcelos M S,Albuquerque E L.Optical transmission spectra in symmetrical Fibonacci photonic multilayers[J].Phys.Lett.A,2009,373(4):496-500.
[9]Kohmoto M,Sutherland B,Iguchi K.Localization in optics:Quasiperiodic media[J].Phys.Rev.Lett.,1987,58(23):2436-2438.
[10]Mao H B,Yang C L,Lai Z S.Theoretical study of the tunable optical filter properties based on photonic crystals[J].Acta Phys.Sinica(物理学报),2004,53:2201-2204(in Chinese).
[11]Ooi C H R,Yeung T C A,Kam C H,et al.Photonic band gap in a superconductor–dielectric superlattice[J].Phys.Rev.B,2000,61(9):5920-5923.
[12]Wu C J,Chen M S,Yang T J.Photonic band structure for a superconductor-dielectric superlattice[J].Physica C,2005,432(1):133-139.
[13]Aly A H,Ryu S W,Hsu H T,et al.THz transmittance in one-dimensional superconducting nanomaterial-dielectric superlattice[J].Mater.Chem.Phys.,2009,113(1):382-384.
[14]Luo Y H,Wang Y S,Wang D D,et al.Optical properties of one-dimensional metallodielectric photonic crystals[J].Spectrosc.Spect.Anal.(光谱学与光谱分析),2008,28(12):256-259(in Chinese).
[15]Cheng C,Xu C,Zhou T,et al.Temperature dependent complex photonic band structures in two-dimensional photonic crystals composed of high-temperature superconductors[J].J.Phys.,2008,20(27):275203-1-8.
[16]Wu C J,Liu C L,Yang T J.Investigation of photonic band structure in a one dimensional superconducting photonic crystal[J].J.Opt.Soc.Am.B,2009,26(11):2089-2094.

