定时截尾下具有缺失数据两个Rayleigh分布总体参数的估计和检验

赵志文,M.S.Abdalroof,盛丹姝

(1.吉林大学 数学学院,长春 130012;2.吉林师范大学 数学学院,吉林 四平 136000)

数据缺失问题是统计学中的常见问题,如在产品的寿命实验中,由于观测方法、实验设备或其他原因常会导致某些实验观测数据缺失,因此对不完全数据的处理是统计学的一个重要研究领域[1].此外,在可靠性寿命实验中,为减少人力、物力及财力的浪费,实验者常会采用定时或定数截尾实验[2-4].当产品的寿命分布为Rayleigh分布时,文献[5]讨论了具有缺失数据的两个Rayleigh分布总体参数的估计问题及两总体参数相等的假设检验问题.对于定数截尾数据,Harter等[6]给出了未知参数的极大似然估计;Howlader等[7]进一步讨论了未知参数的Bayes估计及未来观测值的预测问题.对于步进删失样本,Wu等[8]考虑了未知参数的Bayes估计及未来观测值的预测区间问题.本文在此基础上进一步讨论定时截尾下,具有缺失数据的两个Rayleigh总体参数的极大似然估计及两个总体参数相等的假设检验问题,给出了参数的极大似然估计量,并证明了估计量的强相合性、渐近正态性及检验统计量和检验统计量的极限分布.

1 极大似然估计及其渐近性质

下面考虑参数λ1的极大似然估计.在得到观测值(Zi,δi,αi)(i=1,2,…,n)后,相应的似然函数为

其中:Ai=αiδi(αiδi+1)/2;Bi=αiδi(αiδi-1)/2;i=1,2,…,n.进一步,取对数有

同理,基于样本观测值(Mj,ηj,βj)(j=1,2,…,n),可得参数λ2的极大似然估计

(1)

其中:Cj=βjηj(βjηj+1)/2;Dj=βjηj(βjηj-1)/2;j=1,2,…,n.

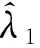
证明:由于{αiδi,1≤i≤n}为独立同分布的随机变量序列,故由强大数定律知

由Slusky定理可知

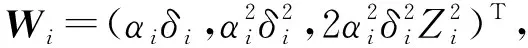
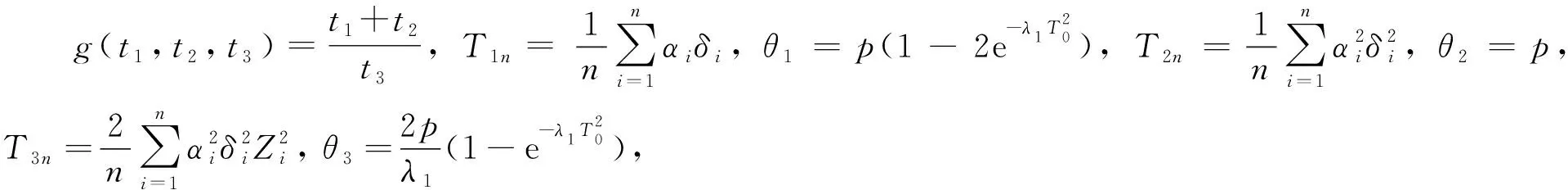
由引理1可知

其中

2 两个总体参数相等的检验及两个总体参数之差的渐近置信区间

在实际问题中,人们通常关心两组样本是否来自同一个总体,该问题可以归结为假设检验:H0:λ1-λ2=0 ↔H1:λ1-λ2≠0.

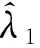
(2)

特别地,在原假设H0下,有

(3)

证明：由命题1和命题2可知

由Slutsky定理可知式(2)成立.证毕.

因此,对于给定的置信水平α,Δλ的置信区间为

3 随机模拟

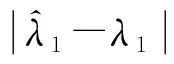
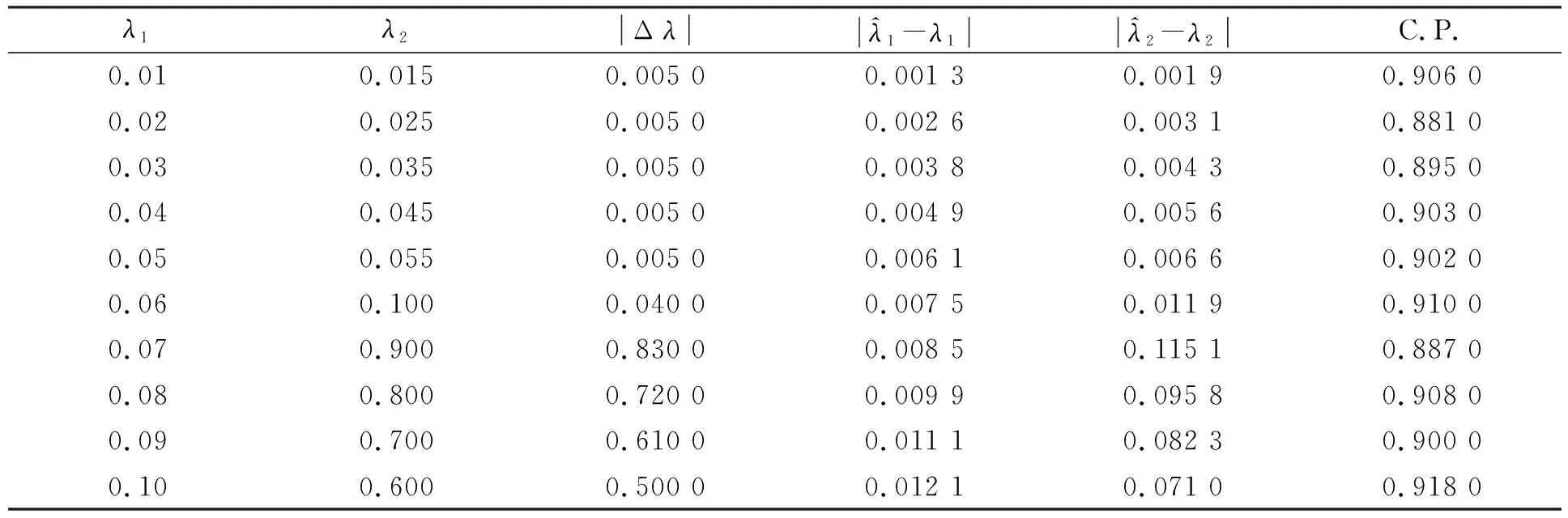
表1 n=50时估计的偏差和覆盖率Table 1 Estimate bias and coverage probability when n=50

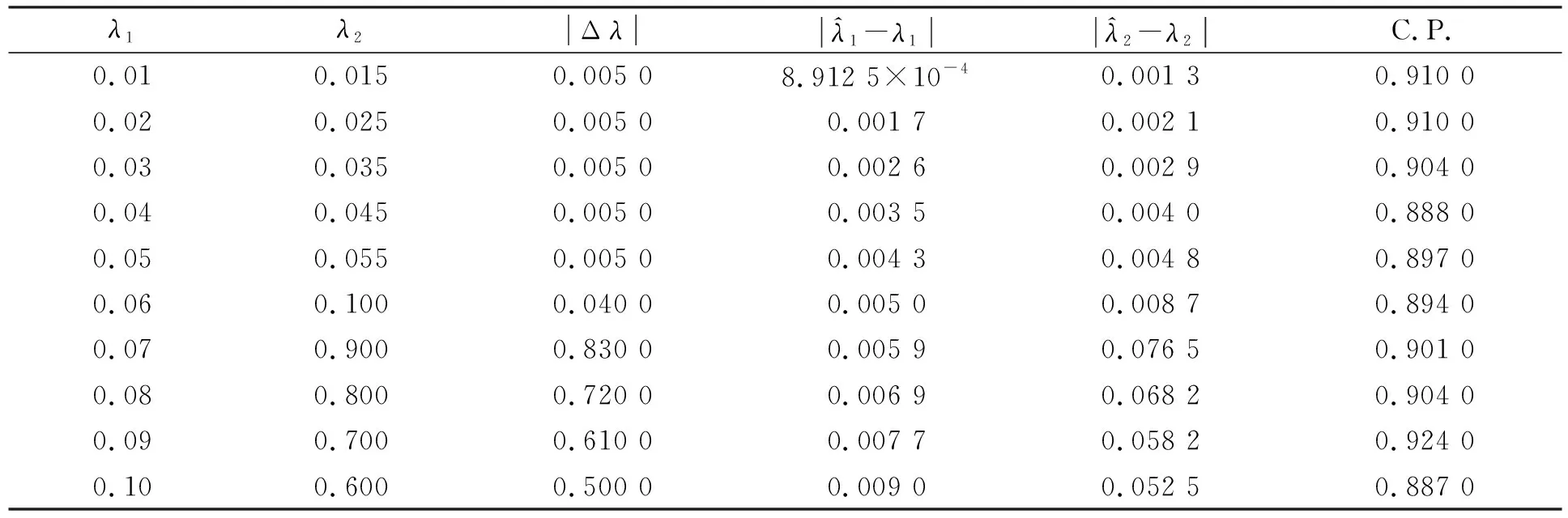
表2 n=100时估计的偏差和覆盖率Table 2 Estimate bias and coverage probability when n=100

表3 n=300时估计的偏差和覆盖率Table 3 Estimate bias and coverage probability when n=300

由表1～表3可见,无论对于较小的样本量还是较大的样本量,本文的估计方法都有较小的误差,并且|Δλ|的置信区间覆盖率非常接近置信水平0.90,表明本文方法具有较高的精度.

[1] Little R J A,Rubin D B.Statistical Analysis with Missing Data [M].New York:John Wiley &Sons,2002.

[2] SUN Xiao-qian,ZHOU Xian,WANG Jing-long.Confidence Intervals for the Scale Parameter of Exponential Distribution Based on Type Ⅱ Doubly Censored Sample [J].Journal of Statistical Planning and Inference,2008,138(7):2045-2058.

[3] ZHAI Wei-li,MAO Shi-song.Parameter Estimation of Exponential Distribution with Two Parameters under Type Ⅰ Censoring Sample [J].Chinese Journal of Applied Probability and Statistics,2002,18(2):197-204.(翟伟丽,茆诗松.定时截尾场合下双参数指数分布的参数估计 [J].应用概率统计,2002,18(2):197-204.)

[4] ZHANG Zhi-hua.Comparison of Optimum Design of Accelerated Life Tests [J].Chinese Journal of Applied Probability and Statistics,2001,17(3):303-307.(张志华.定时截尾情况下简单加速寿命实验优化设计的比较 [J].应用概率统计,2001,17(3):303-307.)

[5] ZHAO Zhi-wen,FU Zhi-hui.Parameter Estimation and Hypothesis Testing of Two Rayleigh Populations with Missing Date [J].Journal of Beihua University:Natural Science,2008,9(3):202-204.(赵志文,付志慧.具有部分缺失数据的两个瑞利分布总体参数的估计与检验 [J].北华大学学报:自然科学版,2008,9(3):202-204.)

[6] Harter H L,Moore A H.Point and Interval Estimators,Based onmOrder Statistics,for the Scale Parameter of a Weibull Population with Known Shape Parameter [J].Technometrics,1965,7(3):405-422.

[7] Howlader H A,Hossain A.On Bayesian Estimation and Prediction from Rayleigh Based on Type Ⅱ Censored Data [J].Communications in Statistics:Theory and Methods,1995,24(9):2251-2259.

[8] Wu S J,Chen D H,Chen S T.Bayesian Inference for Rayleigh Distribution under Progressive Censored Sample [J].Applied Stochastic Models in Business and Industry,2006,22(3):269-279.

[9] 茆诗松,王静龙,濮小龙.高等数理统计学 [M].北京：高等教育出版社,2000:116-118.

(责任编辑：赵立芹)

研究简报