计算软件Maple在线性代数教学中的应用*

刘转玲

(兰州商学院 信息工程学院,甘肃 兰州730020)

计算软件Maple在线性代数教学中的应用*

刘转玲

(兰州商学院 信息工程学院,甘肃 兰州730020)

线性代数教学面临计算量大且繁琐、内容抽象的困扰，借助于计算软件Maple可以使问题很方便地得以解决，使学生有更多时间掌握数学原理和思想，并能够激发学生的学习兴趣，提高课堂教学质量．通过举例，说明了Maple在演示矩阵的初等变换、求解线性方程组、计算矩阵的特征值和特征向量以及作图等方面的应用．

矩阵；初等变换；线性方程组；Maple.

引言

Maple是一种偏于逻辑运算的计算软件[1]，覆盖几乎所有的数学领域，如：微积分，线性代数，方程求解，积分和离散变换，概率论和数理统计，物理，图论等．它高精度的数值计算及强有力的符号计算，高效的编程功能及灵活的图形显示，都有助于学生对于微积分、解析几何、线性代数及概率统计中的常见计算问题的理解，为解决上述问题提供有效的途径．

数学课，被大多学生认为理论性强 、枯燥乏味，一直以来学生只是被动地接受老师所讲，从而长期以来失去对数学的主观能动性学习和兴趣．通过在课堂中渗透Maple知识，包括特定主题的计算方法信息和求解步骤，插入图形或三维动画，使得学生逐渐喜欢数学，从而变被动学习为主动学习．以下就几个例子来说明Maple在线性代数教学中的应用．

1 Maple在线性代数教学中的应用

1.1用Maple演示矩阵的初等变换

在线性代数中，矩阵A的初等变换对于求矩阵A的秩、判定向量组的线性关系、解线性方程组等问题都非常重要，而矩阵的初等变换相对也比较灵活且繁琐，故老师在教学中一般省略掉好多步骤，而用Maple解决此类问题就非常方便．

在Maple系统中可以如下输入：

gt; with(linalg);

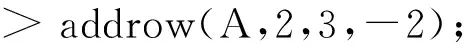
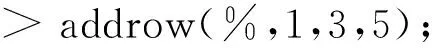
由上面的结果，很容易得A的秩为3．而判定向量组的线性关系、解线性方程组等问题都可转化成相对应矩阵的初等变换，所以此类问题也就很容易在图片的演示中掌握其中的数学原理．

1.2运用Maple求解线性方程组

通过调用命令LinearSolve可以选择合适的算法求解线性方程组．

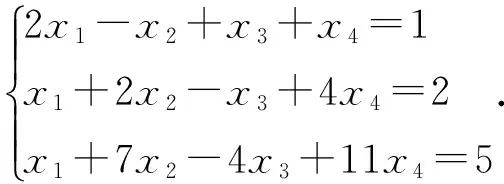
在Maple系统中可以如下输入：

gt; with(LinearAlgebra);

gt; A,B:=lt;lt;2|-1|1|1gt;,lt;1|2|-1|4gt;,lt;1|7|-4|11gt;gt;,lt;1,2,5gt;;

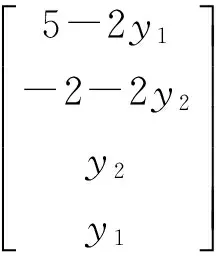
上面的演示，更加清楚地说明：当线性方程组有无穷组解时，自由未知量选择的“自由”性．

1.3计算矩阵的特征值和特征向量

求解一个方阵的特征值和特征向量时，许多同学解不出特征值，这显然影响到求解和理解特征向量，但课堂上借助于Maple就非常容易，从而可以节省更多时间来加深对特征值和特征向量的理解．

在Maple系统中可以如下输入：

gt; with(LinearAlgebra);

gt; CharacteristicPolynomial(A,x); -2+x3-4x2+5x

gt; factor(%); (x-2)(x-1)2

gt; Eigenvalues(A,output=list); [2,1,1]

gt; Trace(A); 4

上面的结果清楚反映了特征向量与特征值的“匹配性”，而这一点在一般课堂教学中最容易被忽略．

1.4Maple作图

例4 用Maple作出偏微分方程(x2+y2+z2)zx-2xyzy-2xz=0的解曲面的图像．

在Maple系统中可以如下输入：

gt;pde:=(x^2+y^2+z(x,y)^2)*diff(z(x,y),x)-2*x*y*diff(z(x,y),y)-2*x*z(x,y)=0;

gt; PDEtools[PDEplot](pde,[t,t,sin(Pi*t/0.1)/10],t=0..0.1);

通过上述命令可以作出偏微分方程(x2+y2+z2)zx-2xyzy-2xz=0的解曲面的图像，见图1．

图1：(x2+y2+z2)zx-2xyzy-2xz=0的解曲面的图像

2 结论

总之，Maple为线性代数教学提供了一个非常好的平台，它的最大优点就是符号功能强大，便于操作，更有利于在教学中突出重点，吸引学生的注意力，使学生由被动学习数学转变为主动学习数学，充分调动学生学习数学的积极性，从而提高课堂学习效率．

[1]张韵华，王新茂．符号计算系统Maple教程[M]．合肥：中国科学技术大学出版社，2007．

[2]李振东，李金林．线性代数[M]．北京：科学出版社，2010．

TheApplicationofMapleinLinearAlgebraTeaching

LIU Zhuan-ling

(Information Engineering College of Lanzhou University of Finance and Economics, Lanzhou Gansu 730020,China)

Linear algebra teaching is facing a large amount of calculation and cumbersome, abstract puzzle,with the help of Maple software, can make the problem easy to solve, help students to have more time to master the mathematical principles and ideas, and can stimulate students’ interest in learning, and improve teaching quality. By way of example, has explained the application characteristics of Maple elementary transformation, in the presentation matrix of solving linear equations, the calculation of matrix eigenvalue and eigenvector and mapping etc.

matrix; elementary transformation; linear equations; Maple.

1673-2103(2013)05-0075-04

2013-09-15

兰州商学院2012年度教学改革研究一般资助项目(20120213)

刘转玲(1977-),女,陕西渭南人,讲师,硕士,研究方向：数学物理方程．

O151.2;G642.0

A