不同时间戳的地图差异匹配改进算法

杜庆峰，赵亚男

（同济大学 软件学院，上海201804）

可升伸缩矢量图形（SVG）是一种使用XML 来描述二维图形及其应用的语言.一个SVG 文档可以被解析成一棵倒立的树形结构，与XML文档的差异匹配算法类似.XML文档的差异匹配算法可以分为3类：第1类是针对有序节点树的差异匹配算法，第2类是针对无序节点树的差异匹配算法，第3类算法不是将XML结构树中所有节点看作有序节点或者全部看作无序节点.

针对有序节点树，Cobena等［1］提出了一种检测XML文档变化算法XyDiff.该算法首先采用自底向上的方式计算每个结点的签名（hash值）和权重（子树的大小），然后从2个文档的根结点开始比较2个结点的签名.由于在算法中使用了贪婪规则，XyDiff不能保证任何形式的最优和近似最优的匹配检测.该算法的时间复杂度为O（nh），其中n为节点个数，h为树的高度.

针对无序节点树，Wang 等［2］提出了X－Diff算法，该算法采用自顶向下的匹配机制，对XML 结构树进行“最小修改代价”搜索匹配，该算法是针对无序节点树的匹配检测最快的算法.该算法的时间复杂度为O（n2dlgd），其中d为最大深度.

第3种算法是由Al－Ekram 等［3］提出 的DiffX算法，该算法根据节点的不同类型将其分为元素节点、属性节点和文本节点，DiffX 算法将元素节点看成有序节点而将属性节点看成无序节点，这样的数据模型更符合XML文档的性质.该算法的时间复杂度为O（n2）.

现有的DiffS［4］算法是在DiffX 算法的基础上定义宏元素节点，以元素节点或宏元素节点作为最小匹配 元 素，创 建2 个 以｛id：String，et：String，e：Element｝为元素的数组E1，E2.该算法的时间复杂度降低至O（nlgn）.

在现有的DiffS算法中，数组E1，E2 中的元素个数太多，导致数组排序和查找的时间太长.另外，对于数组中的每个元素节点，它们的属性字符串太长，导致属性排序的时间也太长.

考虑到现有研究存在的不足，可以重新定义宏元素节点，提出一种新的元素节点：节点集元素，达到减少数组元素个数、降低数组排序和查找时间的目的.另外，通过一种标号定义规则来重新标识SVG结构树，使得属性字符串的长度大大缩短，达到减少属性排序时间的目的.

1 改进算法I－DiffS的思想及实现

1.1 I－DiffS算法思想

1.1.1 相关定义

（1）节点集元素.在某时间戳的SVG 格式地图对应的倒状解析［5］结构树中，从根节点开始将某特定的分支中的元素节点、属性节点和值节点看成一个整体，称为节点集元素.如某id为c2的节点集元素，它的元素节点集合为｛I，J，J，C｝，属性节点为“SY”，值节点为“rgb（0，255，255）60”.

（2）倒状解析结构树标号规则.在SVG 格式地图中主要包括基本图形元素集｛line，rect，circle，eclipse，polyine，polygon，path，text｝，常见框架元素集｛SVG，g，defs，use，symbol，desc，title，image｝，常用属性元素集｛x，y，r，rx，ry，width，height，stroke／style，fill，tspan｝.共有26个主要基本元素，可以用1位大写字母标识，在这26个主要基本元素之外的元素可用1位小写字母标识，如果1位字母标识完毕，可采用2位或多位字母标识，以此类推.

按照倒装解析结构树的标号定义规则，主要基本元素的标号定义如表1.

1.1.2 算法思路和实现

（1）优化后的解析结构树.将原SVG 文件通过节点集元素的定义来得到一棵SVG［6］节点集元素结构树，之后再根据倒装解析树的标号定义规则将SVG 节点集元素结构树转化成优化后的标号节点集元素结构树.

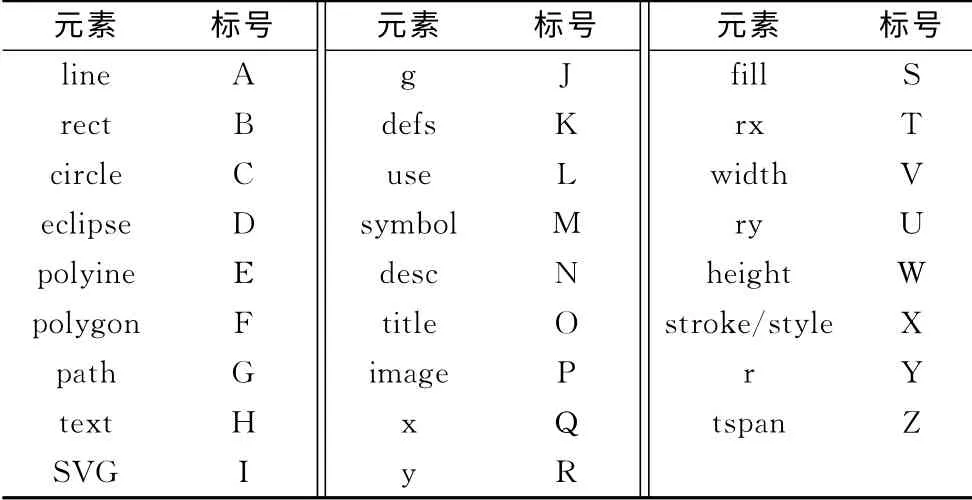
表1 SVG 格式地图主要基本元素的标号定义Tab.1 Labeling rule of major basic labeling rule of major basic element on SVG map

（2）生成匹配节点集元素集合M.首先对SVG［7］格式地图文档对应的结构树中的属性元素节点（除id属性外）按字典顺序排列，该属性元素节点对应的值节点按照排序好的属性元素节点顺序排列.如，一个属性元素节点排序前为“SWV”，排序后为“SVW”，则值元素节点为“none100100”.

接着创建2个以节点集元素为元素的数组E1，E2；E1 中数组个数等于第1 个版本SVG 格式地图［8］对应的树结构中节点集元素的个数m1，同理E2中数组个数等于第2个版本SVG 格式地图对应的树结构中节点集元素的个数m2.

数组E1和E2 中元素的属性由以下6 部分构成：第1个字符串是节点集元素的id值；第2个字符串是节点集元素的元素节点所组成的字符串path；第3个字符串是节点集元素的属性节点所组成的字符串et；第4个字符串是节点集元素的值节点所组成的字符串value；第5个指针用来记录所对应的节点集元素的指针e；第6个是用来记录所对应节点集元素的头指针h，指向一个由元素节点指针所组成的链表；第7个是一个数组flag，用来记录节点集元素的元素节点使用次数，数组flag中的元素初始值为零.

如某节点集元素在数组E1中的表示为：该节点集元素的id值为c2，元素节点所组成的字符串path为“IJJC”，属性节点所组成的字符串et为“SY”，值节点所组成的字符串value为“rgb（0，255，255）60”，该节点集元素的指针e为A11，指向元素节点指针所组成的链表的头指针h为→A1→A4→A8→A11，用来记录各元素节点使用次数的数组flag的长度为4，其中flag［A1］的值为9，flag［A4］的值为2，flag［A8］的值为2，flag［A11］的值1.

对数组E2 中数组元素依据id值进行排序，这样无id值的数组元素被全部排在数组元素的前面，接着对前面无id值的数组元素依据path值进行排序.

依次遍历E1数组元素，如果当前数组元素s对应的树结构的节点集元素已经在匹配节点集元素集合M当中（即s.e∈Array（M.X）），则结束本次循环进入下一次循环，否则继续；当s的id不为空时根据id对数组E2进行折半查找得到数组元素d，其中元素d和s的id值、path值、et值和value值均相等；当s的id为空时根据path折半查找得到元素，其中元素d和s的path值、et值和value值均相等；同时遍历d.h和s.h所对应的2个链表，如果2个链表中对应的每一项都相同，则将（s.e，d.e）合并入匹配节点集元素集合M.该子算法的具体实现（伪代码）如下，其中序号为数值标号.

（3）依据匹配节点集元素集合M生成差异脚本.该算法是以子算法I－SVG－Match得到的匹配节点集元素集合M为基础，首先，对SVG1对应的结构树进行遍历，如果被遍历的节点集元素在SVG2中不能找到对应的节点集元素对在匹配节点集元素集合M中，则对于SVG1中被遍历的节点集元素s，顺序遍历节点集元素头指针s.h所指向的链表，每当遍历到链表中一个指针对应的元素节点时，如果该元素节点的flag 值为1，则在DiffXml中加入delete操作，同时对SVG1 的副本SVG0 所对应的结构树执行delete操作，并对链表中的每个元素节点的flag值做减1操作；否则，不执行任何操作.不断循环此过程，直到遍历到null停止.其中对于与属性节点相邻的元素节点执行delete操作时，除了删除该元素节点之外，还要将与其相邻的属性节点和值节点也一并删除.

接着，对SVG2对应的结构树进行遍历，如果被遍历的节点集元素在SVG1没有对应的节点集元素构成的节点集元素对在匹配节点集元素集合M中，则对于SVG2中被遍历的节点集元素d，顺序遍历节点集元素头指针d.h所指向的链表，每当遍历到链表中一个指针对应的元素节点时，如果该元素节点的flag值为零，则在DiffXml中加入insert操作，同时对SVG1 的副本SVG0 所对应的结构树执行insert操作，并对链表中的每个元素节点的flag值做加1操作.不断循环此过程，直到遍历到null停止.其中对于与属性节点相邻的元素节点执行insert操作时，除了添加该元素节点之外，还要将与其相邻的属性节点和值节点也一起添加进去.

算法执行后生成差异脚本文件DiffXml算法对SVG0的操作结果就是SVG2格式地图对应的结构树，这说明可通过对SVG1 的结点树施加DiffXml脚本中的操作可以再现第2版本地图SVG2.该子算法的具体实现（伪代码）如下.

1.2 I－DiffS算法复杂度

1.2.1 时间复杂度

在算法I－DiffS中，假设SVG1中的元素个数为n1，节点集元素个数为m1；SVG2 中的元素个数为n2，节点集元素个数为m2.并假设SVG1 中每个节点集元素的最大属性个数为ta，SVG2中每个节点集元素的最大属性个数为tb；SVG1的最大深度为d1，SVG2的最大深度为d2.

在I－DiffS的子算法I－SVG－Match中的第5行，对SVG1和SVG2中节点集元素的属性节点排序，时间复杂度近似为m1O（talgta）＋m2O（tblgtb）.第10～19行，深度遍历SVG1和SVG2，并将SVG1和SVG2中的节点集元素添加到SVG1对应的数组E1和SVG2中的数组E2 中，时间复杂度为O（n1）＋O（n2）.第20～21行，依据id值对数组E2进行排序，时间复杂度为O（m2lgm2）.第24～43 行，遍历E1，对于E1中的每一个元素在E2中查找与之匹配的元素，由于E2已经排好序，每次查找时间复杂度为O（lgm2），循环的总的时间复杂度为O（m1lgm2）.因此，子算法I－SVG－Match的总的时间复杂度为

I－DiffS的子算法I－SVG－DiffScript中，第6～21行，遍历SVG1，如果被遍历的节点集元素在SVG2中不能找到对应的节点集元素对在匹配节点集元素集M中，再顺序遍历该节点集元素头指针所对应的链表，时间复杂度近似为O（m1d1）≈O（m1）；第22～37行，遍历SVG2，对于每一个在匹配节点集元素集合M中找不到配对的节点集元素，再顺序遍历该节点集元素头指针所对应的链表，时间复杂度近似为O（m2d2）≈O（m2）.因此子算法I－SVG－DiffScript的总的时间复杂度为O（m1＋m2）.

基于以上分析，算法I－DiffS的总的时间复杂度为O（n）＋O（m1＋m2）≈O（n）.

1.2.2 空间复杂度

数组E1，E2对应SVG1和SVG2，所需的空间复杂度为O（m1＋m2）.SVG0为SVG1对应的副本，所需空间为O（m1）.最坏情况下，E1中的所有元素能在E2中找到匹配节点集元素，因此得到的匹配节点集元素集合M所需的空间复杂度为O（m1）.因此算法I－DiffS 最坏情况下的空间复杂度为O（m1＋

2 I－DiffS算法的验证

2.1 算法验证SVG 原文件

这里验证的是一幅2个不同时间戳的SVG 格式的地图文件，文件名分别为FirstTimestamp.SVG和SecondTimestamp.SVG.

2.2 通过定义节点集元素得到的结构树

图1是文件SVG1和SVG2在定义了节点集元素之后得到的解析结构树，其中椭圆表示元素节点，矩形表示属性节点和其对应的值节点，虚线标出的是文件SVG1和SVG2存在的差异.

2.3 通过标号的定义规则得到的优化后的结构树

图2使用了倒装解析结构树标号定义规则对图1的解析结构树进行了优化，并将图1中属性节点和值节点组成的矩形进行了分离，使用圆形表示元素节点和属性节点，使用矩形表示值节点，每个与矩形相邻的圆形即为属性节点，其余圆形为元素节点.其中属性元素节点中属性顺序按字典顺序排序，值节点中值的顺序按属性节点顺序对应排列.每个元素节点旁边由An（n＝1，2，…，13）和Bn（n＝1，2，…，13）标出该元素节点的指针（如A1，A2等和B1，B2等），用虚线标出文件SVG1和SVG2的差异.

2.4 生成的节点集元素数组

表2和表3中的E1和E2是由优化后的SVG1和SVG2解析结构树生成的数组，数组的元素为节点集元素，每个元素由7种属性构成，分别是节点集元素id、节点集元素的元素节点所组成的字符串path、节点集元素的属性节点所组的字符串et、节点集元素的值节点所组成的字符串value、节点集元素的指针e、节点集元素的元素节点指针所构成的链表的头指针h以及记录了节点集元素的各元素节点使用次数的数组flag.其中数组E2是通过id值按字典顺序排序后生成的.

图1 SVG1和SVG2对应的解析结构树Fig.1 Structural tree corresponding to SVG1and SVG2

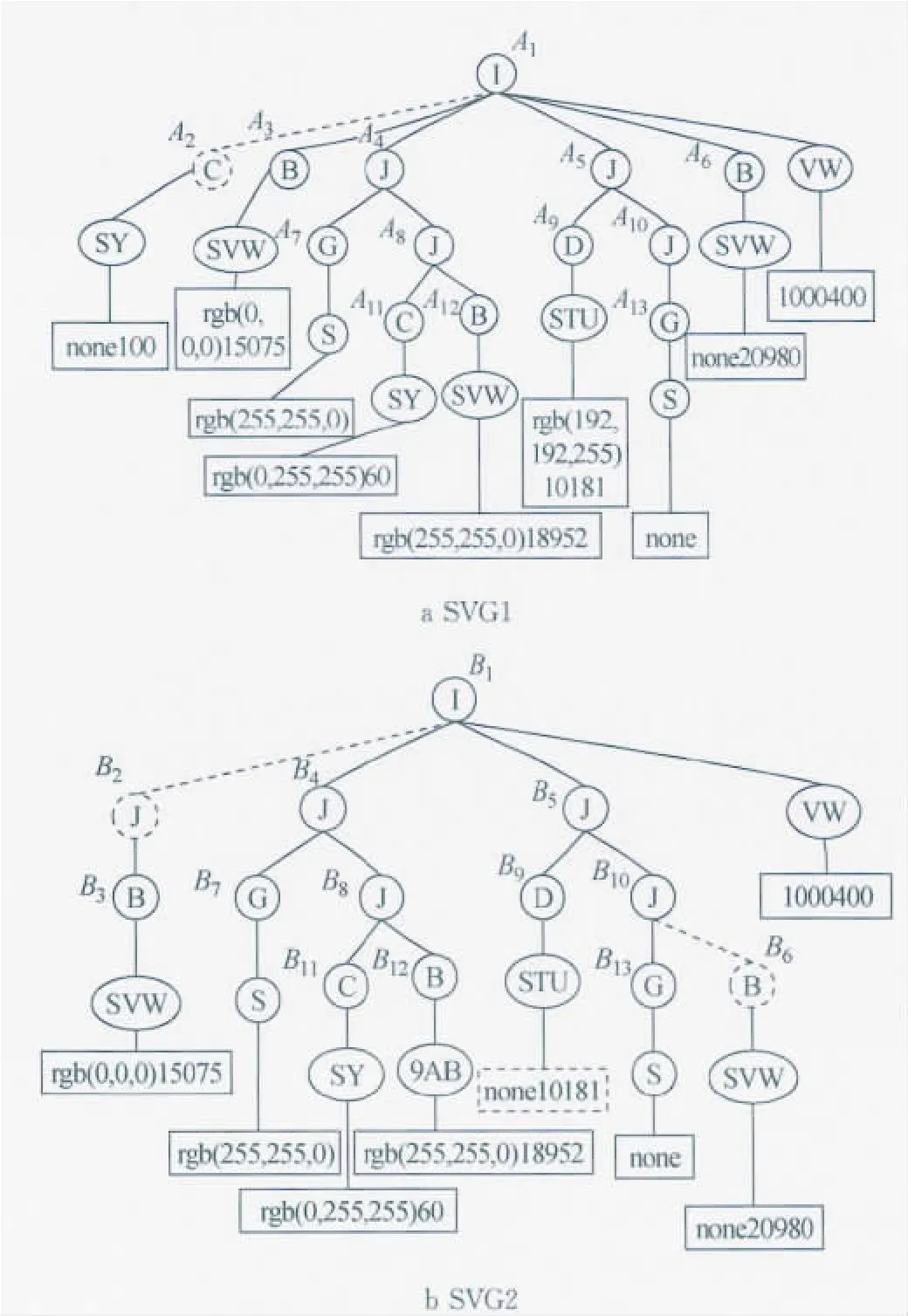
图2 基于SVG1和SVG2优化后的定义了节点集元素的结构树Fig.2 Structural tree corresponding to SVG1and SVG2including node set elements

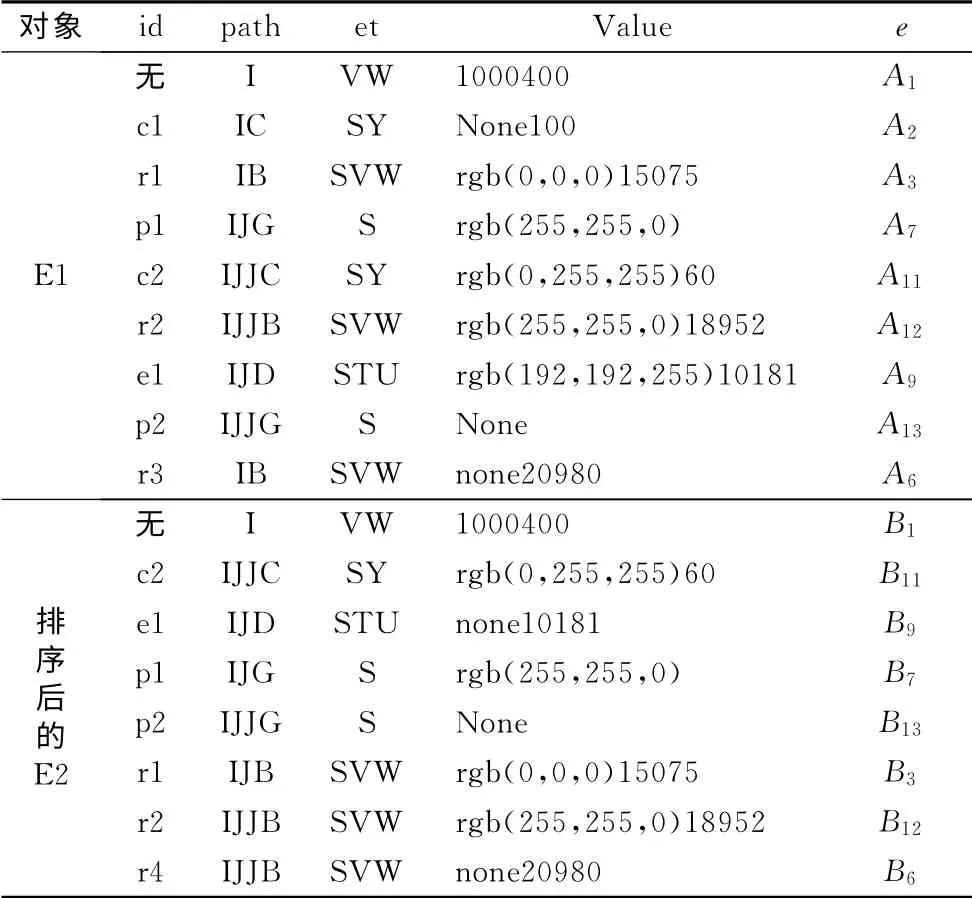
表2 依据节点集元素的属性节点排序后SVG1对应的结构树生成的数组E1和E2Tab.2 Array E1 and E2 corresponding to SVG1 and SVG2including sorted attribute nodes in node set elements

2.5 生成的匹配节点集元素集合M

I－SVG－Match执行匹配过程：当遍历到E1［0］时，M＝｛（A1，B1）｝；当遍历到E1［1］时，M＝｛（A1，B1）｝；当遍历到E1［2］时，M＝｛（A1，B1）｝；当遍历到E1［3］时，M＝｛（A1，B1），（A7，B7）｝；当遍历到E1［4］时，M＝｛（A1，B1），（A7，B7），（A11，B11）｝；当遍历到E1［5］时，M＝｛（A1，B1），（A7，B7），（A11，B11），（A12，B12）｝；当遍历到E1［6］时，M＝｛（A1，B1），（A7，B7），（A11，B11），（A12，B12）｝；当 遍 历 到E1［7］时，M＝｛（A1，B1），（A7，B7），（A11，B11），（A12，B12），（A13，

B13）｝；当遍历到E1［8］时，M＝｛（A1，B1），（A7，B7），（A11，B11），（A12，B12），（A13，B13）｝.以上是执行子算法I－SVG－Match第24～43行的循环过程，最终得到匹配节点集元素集合M.

表3 依据节点集元素的属性节点排序后SVG2对应的结构树生成的数组E1和E2Tab.3 Array E1 and E2 corresponding to SVG1 and SVG2including sorted attribute nodes in node set elements

2.6 生成的差异脚本I－DiffXml

子算法I－SVG－DiffScript依据匹配节点集元素集合M对SVG1对应的结构树进行遍历，其中节点集元素A2，A3，A9，A6不在集合M中，则首先访问A2.h指向的元素节点指针链表，由于flag［A2］的值为1，则在I－DiffXml脚本中加入了对SVG1中的A2执行delete的操作，并对flag［A1］和flag［A2］做减1操作，flag［A1］的值为8，flag［A2］的值为零；接着顺次访问A3.h，A9.h和A6.h指向的元素节点指针链表，执行的操作步骤同理；此时在I－DiffXml中已加入了对SVG1中的A2，A3，A9，A6执行delete的操作，即在SVG1 对应的结构树中删除了A2，A3，A9和A6，并且flag［A1］的值为6，flag［A2］的值为零，flag［A3］的值为零，flag［A5］的值为1，flag［A9］的值为零，flag［A6］的值为零.

接着，对SVG2对应的结构树进行遍历，其中节点集元素B3，B9，B6不在集合M中，则首先访问B3.h指向的元素节点指针链表，由于flag［B2］初值为零，则在I－DiffXml脚本中加入了SVG2中的B2，由于flag［B3］初值为零，则在I－DiffXml脚本中加入了SVG2中的B3；接着顺次访问B9.h和B6.h指向的元素节点指针链表，执行的操作步骤同理，即在IDiffXml脚本中加入了SVG2中的B2，B3，B9和B6.I－DiffXml差异脚本的具体实现如下.

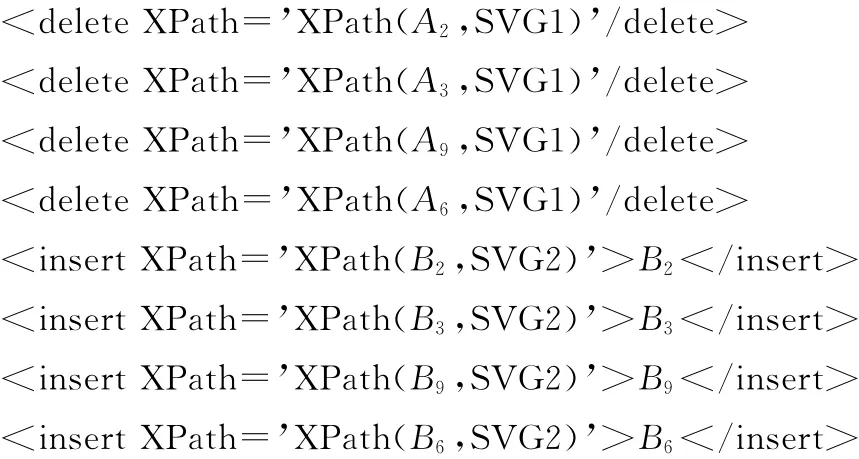
3 结论

在现有的SVG（XML）差异算法的基础上着重分析了目前最新的DiffS算法，并提出了一种改进算法I－DiffS.该算法主要对以下几方面进行了改进：①定义了节点集元素，减少了结构树对应数组的元素个数，缩短了匹配过程；②使用了基于结构树的标号定义规则，使得原本的结构树得到了进一步的优化，减少了排序时间；③算法复杂度为O（n），低于现有的最优匹配算法DiffS的时间复杂度O（nlgn），适合对大规模SVG 格式地图进行差异匹配；④由于定义了节点集元素，差异脚本中的操作由原本的insert，move和delete 3种操作转变成insert和delete 2种操作.该算法为今后基于SVG 的相关研究提供了理论基础.

［1］ Cobena G，Abiteboul S，Marian A.Detecting changes in XML documents［C］／／Proceedings of the 18th International Conference on Data Engineering.San Jose：IEEE，2002：1－3.

［2］ Wang Y，DeWitt D，Cai J.X－Diff：an effective change detection algorithm for XML documents［C］／／Proceedings of the 19th International Conference on Data Engineering.Bangalore：IEEE，2003：2－4.

［3］ Al－Ekram R，Adma A，Baysal O.diffX：an algorithm to detect changes in multi－version XML documents［C］／／Proceedings of the 2005 conference of the Centre for Advanced Studies on Collaborative Research.Markham：IBM，2005：5－10.

［4］ Du Q，Guo ZC，Tang X.DiffSvg－matching algorithm of different timestamp maps based on SVG ［C］／／IEEE International Conference on Computer Science and Service System，Nanjing：［s.n.］，2012：1－5.

［5］ DU Q，TANG X.The Improvement of VTD－XML processing model［C］／／IEEE International Conference on Computer Science and Service System.Nanjing：IEEE，2011：2－4.

［6］ Tomokazu Fujino.SVG＋Ajax＋R：a new framework for WebGIS［J］.Computational Statistics，2007，22（4）：511.

［7］ YUAN Man，CHEN Xiuhong，YANG Chunling，et al.A practical and light integrated WebGIS based on SVG［C］／／CMC’09 Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing.Kunming：CMC，2009：142－146.

［8］ DONG Xuemin， LI Yan. Standardization of SVG in implementing WebGIS［J］.ESIAT’09 Proceedings of the 2009 International Conference on Environmental Science and Information Application Technology.Wuhan：ESIAT，2009：534－537.