SPATIAL REGULARIZATION OF CANONICAL CORRELATION ANALYSIS FOR LOW-RESOLUTION FACE RECOGNITION

ZhouXudong（周旭东），Chen Xiaohong（陈晓红），Qian Qiang（钱强）

（1.College of Computer Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China；2.Information Engineering College，Yangzhou University，Yangzhou，225127，P.R.China；3.College of Science，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China）

INTRODUCTION

Low-Resolution （LR）faces are common in real world applications，like faces captured in surveillance circumstances.Compared with high-resolution（HR）faces，LR ones lose much facial information（e.g.skin texture）which is crucial for high recognition accuracy.As a result，LR face recognition is a highly challenging problem.To deal with it，there have been a number of methods developed in recent years［1－5］.Canonical correlation analysis（CCA）based method is an important one among these works［2－3］.

CCA［6－7］is a classical but useful multivariate statistical analysis method.It aims to find maximally correlated projections between two sets of variables，which can be considered as two views or representations of the same set of objects.Recently，CCA based methods have been developed for dealing with LR face recognition problem［2－3］.In the realization of these methods，HR faces are incorporated to improve the recognition accuracy of LR faces.Li，et al［2］developed a CCA based approach named coupled mappings（CM）for LR face recognition.CM projected the face images with different solutions（LR and HR）into a unified feature space，in which promising recognition rate was obtained.Further，Huang，et al［3］performed a nonlinear mapping between HR／LR face images via radial basis function（RBFs）in the coherent space obtained by CCA.

Therefore，CCA based methods for LR face recognition involve face images with different res-olutions（or multi-resolutions），i.e.LR and HR.For single-resolution face recognition，researchers have shown that utilizing spatial information as regularization term is beneficial to improving the recognition accuracy，mainly because the pixels of each face are not independent but spatially correlated［8－9］.However，for a multi-resolution scenario，there are no related works.Therefore，a method named spatial regularization of canonical correlation analysis（SRCCA）is developed for LR face recognition to improve the performance of CCA by regularization utilizing spatial information of different resolution faces.It is necessary to mention that SRCCA can be applied to the CCA based methods to improve their performance in LR face recognition，since SRCCA is an elementary algorithm similar to CCA.On the other hand，SRCCA has two spatial regularization terms corresponding to LR and HR respectively，different from single-resolution face recognition research works［8－9］.with only one spatial regularization term.As a result，we empirically analyze the impact of LR and HR spatial regularization terms on LR face recognition，respectively.

1 CANONICAL CORRELATION ANALYSIS

CCA，proposed by Hotelling［6－7］，is a wellknown technique for finding pairs of vectors that maximize the correlation between two sets of paired variables.

To be specific，X＝［x1，…，xn］∈Rdx×nand Y＝［y1，…，yn］∈Rdy×nare the two sets of variables of the same objects，where xi∈Rdxand yi∈Rdy（both with zero mean）corresponding to the ith object.CCA can be defined as the problem of finding apair of canonical basis vectors：wxof dx×1size and wyof dy×1size，such that the projected variables wTxXand wTyY are maximally correlated.The two projection vectors can be acquired by maximizing the following correlation coefficient

Sinceρis invariant to the scaling of wxand wy，CCA can be expressed equivalently as the fol-lowing constrained optimization problem

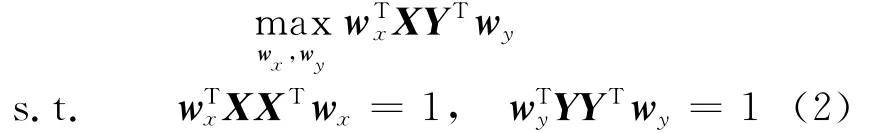
2 SPATIAL REGULARIZATION OF CANONICAL CORRELATION ANALYSIS

In this section，we will first propose SRCCA for LR face recognition and formulate specific learning algorithm by incorporating the spatial information of different resolution faces into CCA framework.And we also show how to solve this problem in a closed form.

2.1 Formulation of SRCCA

For LR face recognition，we use Xand Yto denote LR and HR face training sets，respectively.Each LR face image havepixels（dx＝）and each HR face image have）.

In order to utilize spatial information of face image effectively，we choose the two-dimensional discretized Laplacian smoothing method to measure the smoothness of the basis vectors of the face space along horizontal and vertical directions，which has been successfully used in Refs.［8-9］for single-resolution face recognition.For a function fdefined on a regionΩ，the Laplacian penalty function Jis defined by J（f）＝∫Ω［Lf］2dt，where Lis the Laplacian operator.Thus，J（f）can be used to measure the smoothness of fover the regionΩ.As for images，we utilize the discrete approximation for two-dimensional Laplacian L［8］.For LR face images，it is a dx×dxmatrix

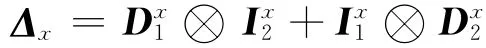
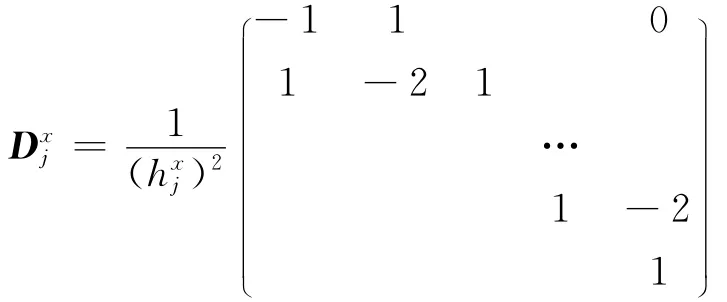
Thus，SRCCA gets developed through incorporating the spatial structure information of different resolution faces as regularization terms into the CCA′s object function Eq.（2）.Its object function is defined as

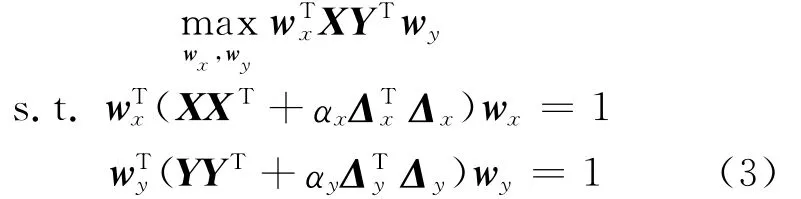
whereαxandαyare balance parameters，which control the smoothness of wxand wy，respectively.Whenαx＝0，SRCCA totally ignores the spatial relationship between pixels of a LR image；Whenαx→∞，SRCCA chooses a spatially smoothest basis vector wxand totally ignores the structure of the LR face data.Similarly for parameter αy.

2.2 Solution of SRCCA

We will solve optimization problem Eq.（3）through Lagrange multiplier method，and its Lagrangian function is defined as

Taking derivatives with respect to wxand wy，respectively，we obtain

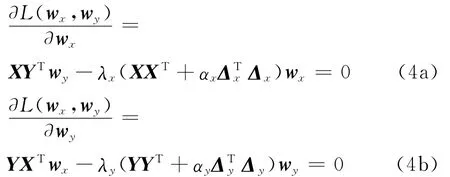
Subtracting Eq.（4a）premultiplied by wTyfrom Eq.（4b）premultiplied by wTx，we have

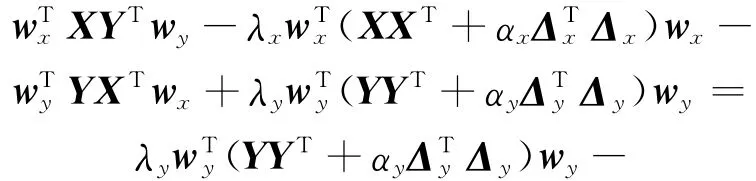
which together with the constraints in Eq.（3）leads toλy－λx＝0.Now letλy＝λx＝λ，we have

Finally，we can recast the optimization problem Eq.（3）as the following generalized eigenvalue problem

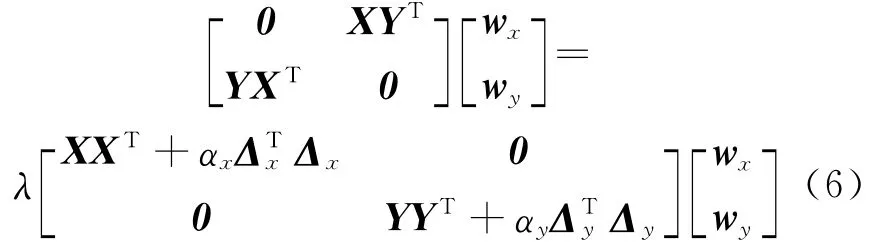
whereλis the generalized eigenvalue corresponding to the generalized eigenvector（wx，wy）.Now taking the top r≤min（dx，dy）generalized eigenvectors，we obtain r-dimensional mappings（Wx∈Rdx×r，Wy∈Rdy×r）.

2.3 Two special cases of SRCCA

Note that SRCCA involves two regularization terms corresponding to HR and LR face spatial information，respectively.In order to analyze the impact of the two regularization terms of SRCCA on LR face recognition，we give two special cases：SRCCA-X and SRCCA-Y.In detail，SRCCA-X only considers LR spatial information regularization term，therefore，its object functions is defined as

And SRCCA-Y only considers HR spatial information regularization term，therefore，its object function is defined as

3 EXPERIMENTAL RESULT AND ANALYSIS

In this section，we evaluate the effectiveness of the proposed SRCCA on three popular face databases including Yale，AR and Extended Yale B.In the experiments，we use the cropped face images with the resolution of 32pixel×32pixel as HR face images and their down-sampling to 12 pixel×12pixel as LR face images.Further，we empirically analyze the impact of LR and HR spatial regularization terms on LR face recognition，respectively.It is necessary to mention that SRCCA can be applied to the CCA based methods to improve their performance in LR face recognition，since SRCCA is an elementary algorithm similar to CCA.As a result，we only compare the proposed SRCCA with CCA in the following experiments.

3.1 Evaluation metric and parameter selection

Evaluation metric：For any test LR sample xi，we firstly extract its features WTxxi，then organize its classification based on WTxXand WTyY，where Xand Yare LR and HR face training sets，respectively.In this paper，the nearest neighbor classifier is employed to estimate the classification accuracies of different methods.

Parameter selection in SRCCA：Parameters αxandαyare both searched from｛2－10，2－8，…210｝.

3.2 Database description

Yale［10］database contains 165face images of 15individuals.There are 11images per subject，and these images are respectively under the following different facial expression or configuration：center-light，wearing glasses，happy，leftlight，wearing no glasses，normal，right-light，sad，sleepy，surprised，and wink.AR database consists of over 4 000color face images of 126 people，including frontal view faces with different facial expressions，illumination，and occlusions.In this experiment，we choose a subset of AR database provided and preprocessed by Martinez［11］.This subset contains 100persons（50men and 50 women）and each person has 14different images taken in two sessions（separated by two weeks）.Each session contains seven images with different illumination and expressions.Extended Yale B［12］database contains 2 414front-view face images of 38individuals.For each individual，about 64pictures are taken under various laboratory-controlled lighting conditions.

3.3 Experimental result

We partition the face images into different training and test sets.Concretely，we conduct three group experiments on each database.For Yale，l（l＝3，4and 5，respectively）images of each individual are randomly selected for training and the rest for testing.For AR，l＝3，5，7.For Extended Yale B，l＝10，15，20.Table 1reports the accuracies averaged over 10independent trials.We provide the highest accuracy under different dimension subspaces.In Table 1，ARR means average recognition accuracy and Std standard deviations.

From Table 1，we can see SRCCA outperforms CCA with different numbers of training samples per individual in all databases.The reason is that SRCCA explicitly takes into accountthe spatial relationship between the pixels in the HR and the LR face image.The use of spatial information significantly reduces the number of degrees of freedom.Therefore，SRCCA can have good performance even when there is only a small number of training samples available.

Table 1 Average recognition accuracy across 10runs and corresponding standard deviations %

3.4 Discussion

In this section，we empirically discuss the impact of LR and HR spatial regularization terms on LR face recognition，respectively.From Table 1，we can obtain the following observations：

（1）SRCCA- X and SRCCA- Y both performs better than CCA in all cases，indicating that spatial information of HR and LR face image are both beneficial to improving the LR recognition accuracy.

（2）SRCCA-Y outperforms SRCCA-X in all cases，which shows that the spatial information description of HR faces is superior to that of LR faces.

（3）The performance of SRCCA-Y is similar to that of SRCCA.This implies that spatial information of LR face in SRCCA is redundancy to some extent.

4 CONCLUSION

In this paper，we propose a novel variant of CCA named SRCCA for LR face recognition.SRCCA can take the advantage of the spatial information of different resolution face images by utilizing the regularization technique.Experimental results on three face datasets show that SRCCA performs better than CCA.As an elementary algorithm similar to CCA，SRCCA can be applied to the CCA based methods to improve their performance in LR face recognition.Through experimental results，we further empirically analyze the impact of LR and HR spatial regularization terms on LR face recognition，respectively.

［1］ Hennings-Yeomans P H，Baker S，Kumar B V K V.Simultaneous superresolution and feature extraction for recognition of low resolution faces［C］∥Proc of IEEE Conference on Computer Vision and Pattern Recognition.Los Alamitos，CA：IEEE Computer Society，2008：1-8.

［2］ Li B，Chang H，Shan S，et al.Low-resolution face recognition via coupled locality preserving mappings［J］.IEEE Signal Processing Letters，2010，17（1）：20-23.

［3］ Huang H，He H.Super-resolution method for face recognition using nonlinear mappings on coherent features［J］.IEEE Transactions on Neural Networks，2011，22（1）：121-130.

［4］ Zhou C，Zhang Z，Yi D，et al.Low-resolution face recognition via simultaneous discriminant analysis［C］∥Proc of International Joint Conference on Biometrics.Los Alamitos，CA：IEEE Computer Society，2011：1-6.

［5］ Zou W W W，Yuen P C.Very low resolution face recognition problem［J］.IEEE Transactions on Image Processing，2012，21（1）：327-340.

［6］ Hotelling H.Relations between two sets of variates［J］.Biometrika，1936，28（3／4）：321-377.

［7］ Hardoon D R，Szedmak S，Shawe-Taylor J.Canonical correlation analysis：An overview with application to learning method［J］.Neural Computation，2004，16（12）：2639-2664.

［8］ Cai D，He X，Hu Y，et al.Learning a spatially smooth subspace for face recognition［C］∥Proc of IEEE Conference on Computer Vision and Pattern Recognition.Los Alamitos，CA：IEEE Computer Society，2007：1-7.

［9］ Hou C，Nie F，Zhang C，et al.Learning an orthogonal and smooth subspace for image classification［J］.IEEE Signal Processing Letters，2009，16（4）：303-306.

［10］Belhumeur P N，Hespanha J O P，Kriegman D J.Eigenfaces vs.fisherfaces：Recognition using class specific linear projection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（7）：711-720.

［11］Martinez A M，Kak A C.PCA versus LDA［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23（2）：228-233.

［12］Lee K C，Ho J，Kriegman D.Acquiring linear subspaces for face recognition under variable lighting［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（5）：684-698.