含裂隙孔隙介质中纵波传播特征研究

杜 伟，邓继新，曲寿利，王世星

（1.成都理工大学地球物理学院，四川成都610059；2.四川省蜀通岩土工程公司，四川成都610000；3.油气藏地质及开发工程国家重点实验室（成都理工大学），四川成都610059；4.中国石油化工股份有限公司石油物探技术研究院，江苏南京211103）

利用地震属性进行裂隙预测需要对含裂隙孔隙介质中弹性波传播特征进行系统研究，并建立介质（裂隙）特征参数与地震波传播特征之间的联系。最常用的裂隙模型主要有Hudson裂隙模型和线性滑动模型两类。其中Hudson裂隙模型是基于散射理论来分析含币形裂隙弹性固体的平均波场特性，而线性滑动—界面裂隙模型是将裂隙看作无限薄的高柔度薄层或满足线性滑动边界条件的“弱”面［1－2］。Bakulin等将 Hudson裂隙模型与线性滑动裂隙模型有机的联系起来，并详细讨论了定向裂隙可能形成的各向异性介质类型及相应地震波传播的规律［3］。

由于含裂隙孔隙介质中孔隙和裂隙在尺度上的差异，在弹性波的作用下介质中会形成介观尺度上的孔隙流体流动，这种流体流动耗散机制可使岩石介质在地震频段也表现出较为明显的速度频散和衰减特征［4－8］。我们将周期性层状孔隙介质中厚度较薄的一层替换为具有高孔隙度的柔性层［9］，即裂隙在背景孔隙介质中呈定向等间距分布，给出含裂隙孔隙介质中纵波衰减和速度频散的理论计算模型，相对于Brajanovski等提出传播矩阵法一文中所介绍的方法［6］更为简洁且物理意义明确。同时，将这种效应与描述裂隙的重要参数联系起来，在一定程度上提高了含裂隙孔隙介质中弹性波传播的预测和模拟的能力，为更有效的利用地震或测井信息进行含裂隙孔隙储层的预测及评价提供依据。

1 含定向裂隙的孔隙介质简化模型

以裂隙型碳酸盐岩储层或碎屑砂岩储层为代表的裂隙孔隙介质通常具有两种孔隙系统。影响储层质量的裂隙为具有一定延展和张开度的介观尺度裂隙（裂隙长度在厘米级到分米级之间），可使用不同纵横比的币形裂隙或满足线性滑动边界条件的无限薄的高柔度“弱面”作为介质中裂隙的理想模型［9］。由于储层中的裂隙在后期地质流体作用下会逐渐在其中沉淀一些重结晶矿物颗粒，这使得裂隙面并非完全相互分离，而是在其延展范围内存在多个相互接触的部位，其形态更类似于具有很高孔隙度而厚度很小的孔隙介质层，因此可将含定向裂隙的孔隙介质等效为由孔隙介质层（背景介质）与高孔隙度软薄层所构成的层状介质。

图1为周期性层状孔隙介质模型，①层和②层的半厚度分别为a与b［9］。如果将该等效体元中较薄一层介质的厚度趋于零，即b→0，则可用该层来表征裂隙。取由①层与②层所构成的等效体元进行分析，在垂直于层面的稳态纵波作用下，外加应力亦与层面垂直，使孔隙介质整体表现为单轴应变状态，同时等效体元中的每一层均满足Biot方程。

图1 周期性层状孔隙介质模型

2 低频条件下裂隙孔隙介质的衰减和频散特征

在文献［1］中推导出的公式基础上，对本文的裂隙孔隙介质模型进行分析。Biot理论时间域弹性动力学方程组可以表示为［10－11］

式中：u为孔隙介质固体骨架位移向量，若定义U为平均流体位移向量，则孔隙流体相对位移向量w＝φ（U－u）；φ为介质孔隙度；ρb和ρf分别代表固体骨架组成物质密度与孔隙流体密度。

作用于孔隙介质上的总应力张量τij与平均孔隙压力p可分别表示为［12］

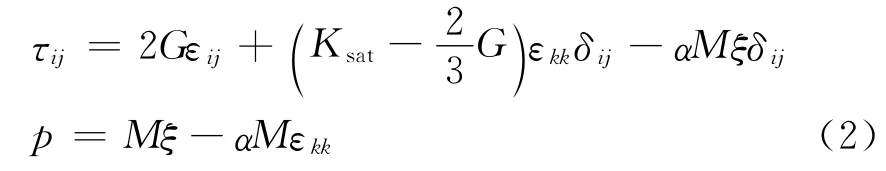
式中：εij为孔隙介质骨架应变张量；εkk＝为孔隙介质固体骨架的体应变；ξ＝Δ（u－U）表示孔隙流体增量。

分别在等效体元的顶、底面沿垂直于层面的z轴方向作用简谐正应力Pe＝－τ0exp （iωt），其中τ0为弹性波振幅。①，②层中的诱发孔压p～1与p～2可表示为

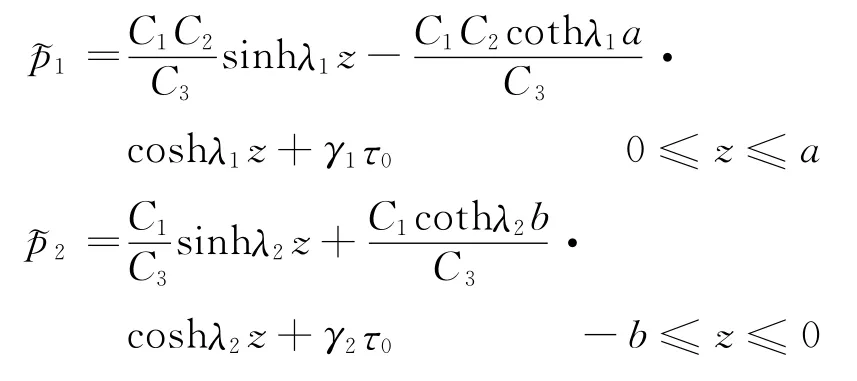
式中：coth为双曲余切函数；κ1和κ2分别为①层与②层孔隙介质的绝对渗透率；γ1和γ2分别为单轴应变条件下①层与②层的Skempton系数。

①，②层的固体骨架位移振幅～u（z），在模型单元边界z＝a处位移振幅（a）为

模型单元边界z＝－b处位移振幅～u（－b）为

式中：Esat2和cm2分别代表②层流体饱和孔隙介质在单轴应变条件下的非排水应变模量与Geertsma系数。公式（4）和公式（5）中的第一项为非排水条件下各层孔隙介质在外加正应力作用下的位移，第二项则为层间流体流动作用所引起的介质固体骨架位移。

定义复纵波模量H（）ω＝－Pe／ε，其中作用于等效体元上的外加应力Pe＝－τ0exp（iωt），可令等效体元的总长度为L，则等效体积模量H（ω）可表示为

利用复体积模量可计算出纵波相速度vp与纵波衰减的逆品质因子Q－1：

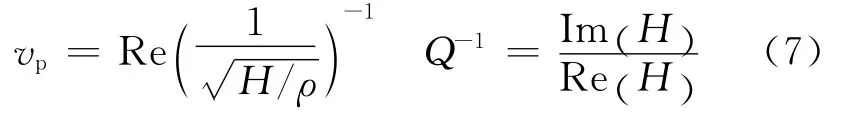
式中：ρ为等效体元的密度。

对周期性层状孔隙介质模型（图1）进行计算，其中①层代表具有较低孔隙度的硬砂层，②层为具有较高孔隙度软砂层或裂隙层，孔隙层均为水饱和。介质模型等效体元的总长度取定值L＝0.2m，其中①层厚度a＝0.18m，②层厚度b＝0.02m。孔隙介质层的骨架参数与饱和流体参数见表1。

图2中给出不同频率下介质模型中归一化孔隙压力（p／Pe）实部变化特征（虚部因其量值很小而未给出）。与参考文献［9］得出的结论一致，在①，②层分界面处（z＝0）形成明显的压力梯度。为平衡快纵波所形成的孔压梯度，孔隙流体以慢纵波的形式发生扩散，致使总孔隙压力（Ⅰ＋Ⅱ）在分界面处达到平衡（慢纵波孔压为公式（3）中前两项）。在相对低频条件下，①，②层中快纵波所形成的压力梯度可通过慢纵波扩散作用平衡，致使总孔隙压力在①，②层内相等且近于恒定，介质体系处于弛豫状态。随频率的增加慢纵波通过流体扩散作用对孔隙压力的影响范围减小，慢纵波所引起的孔隙压力变化仅局限在距离界面较近的范围内（图2c和图2d），在该范围内总孔隙压力迅速变化，而该范围之外总孔隙压力又与快纵波诱发孔隙压力一致，孔隙流体逐渐接近非弛豫状态，此时孔隙介质系统可简单看做是由弹性层叠置构成。

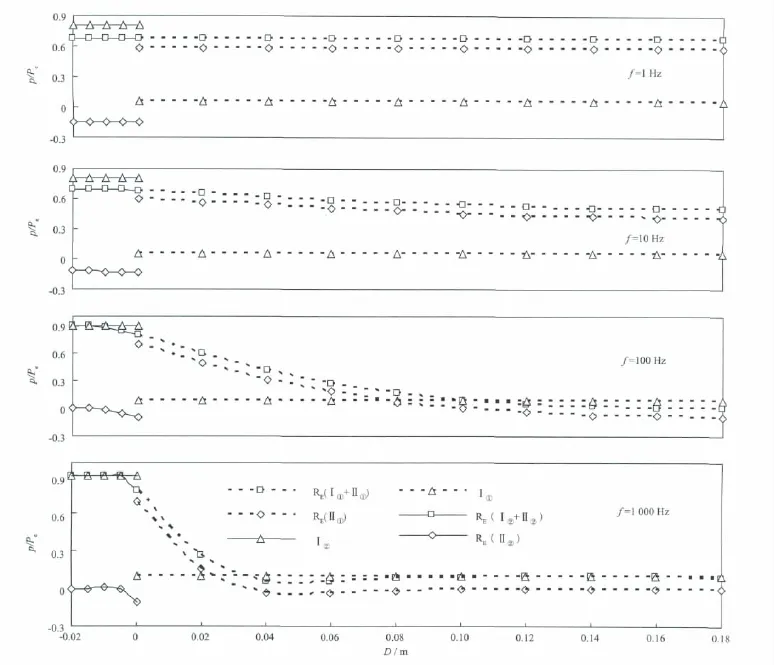
图2 孔隙介质层归一化孔隙压力（p／Pe）实部分布特征

根据公式（2）可知孔隙流体相对运动速度应与孔隙压力的变化率一致。我们所得出的结论与参考文献［9］的结论一致，在此就不再赘述。慢纵波所形成的流体相对流动起主导作用，模型介质中传播弹性波的衰减主要表现为慢纵波的耗散作用。

3 低频条件下裂隙孔隙介质的频散方程

3.1 干燥条件下周期性层状孔隙介质顺度矩阵表示

如果干燥条件下①，②层孔隙介质的体积模量分别为Kb1与Kb2，剪切模量分别为Gb1与Gb2，则在长波长假设下（传播弹性波波长远大于单位体元的长度）周期性层状孔隙介质的等效弹性性质具有横向各项同性介质特征，其顺度矩阵sdry可表示为［14］

式中：参数A＝G／Ksat，B＝3〈G〉－4〈AG〉，“〈〉”代表对应弹性参数的体积加权平均值，如对所研究单位体元〈G〉可表示为

如果用厚度相对较薄的B层来代表裂隙，则其厚度b→0，同时干燥条件下该层介质的体积模量与剪切模量也应趋于零值，即Kb2→0，Gb2→0。利用上述关系可得到如下表达式：

利用公式（10）顺度矩阵sdry可简化为

式中：等号右边第1项为干燥条件下①层孔隙介质顺度矩阵表示形式，其中Yb1与νb1为①层孔隙介质在干燥条件下的杨氏模量与泊松比；等号右边第2项在②层厚度趋于零时可视为因裂隙的存在而形成的附加裂隙顺度。同样，根据线性滑动—界面裂隙模型，对于含周期性定向裂隙的弹性固体其顺度矩阵s亦可以表示为s＝sb＋sc的形式，其中sb为含裂隙背景介质的顺度，其与①层孔隙介质的顺度矩阵在表示形式上相同；sc为裂隙附加顺度，其矩阵形式为［15］

式中：ZN与ZT分别为裂隙法向与切向附加柔度。因此当公式（11）与公式（12）完全对等时，两式中表示裂隙附加顺度的矩阵必须相等，则下列条件成立

3.2 流体饱和裂隙孔隙介质刚度系数C33表示

如果用单位体元中②层孔隙介质代表裂隙，则该层应同时满足层厚b→0及孔隙度φ→1，在孔隙度φ→1时该层的体积模量与剪切模量Kb2和Gb2趋近于0。对于裂隙层则有Biot系数α2→1，孔弹性参数M2＝Kf（Kf为②层裂隙饱和流体的体积模量），裂隙层在非排水条件下的体积模量Ks2at＝M2＝Kf。对于双曲余切函数（cothx）存在关系cothx＝1／x，则有

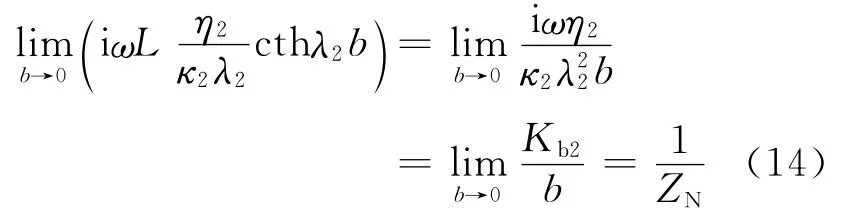
将（14）式代入（6）式中可得到流体饱和条件下裂隙孔隙介质中法向入射纵波的刚度系数C33的计算公式（表示为单轴应变条件：Edry1＝Kb1＋4Gb1／3，Esat1＝Ksat1＋4Gb1／3）：

（15）式与Brajanovski等利用传播矩阵法所推导的计算结果一致［9］。

在公式（15）中垂直裂隙传播纵波的频率ω应满足关系ω＜0.15ωc，此时公式（15）中的刚度系数C33处于频散关系的低频域，在低频极限下有

则在低频极限下刚度系数C33可表示为

当传播纵波的频率ω足够大（但仍满足关系ω＜0.15ωc），即ω≫D2／L2，孔隙压力差异不能够在波传播的半周期内达到平衡，此时刚度系数C33处于频散关系的高频域，高频下双曲余切函数（cothx）存在关系＝－i，则（17）式在高频极限下可表示为

4 数值计算结果及分析

可利用Krief公式计算作为背景层的①层孔隙介质在干燥条件下的体积模量Kb1与剪切模量Gb1，Krief公式表示为［16］：

若分析含周期性定向裂隙的碳酸盐岩储层纵波传播特征，则可取背景孔隙介质组成颗粒为方解石，其体积模量Ks与剪切模量为Gs分别为76.8和32.0GPa［17］。法向与切向附加柔度ZN与ZT的值难以准确给出，因此采用无单位裂隙弱度来表征裂隙的影响，其值变化范围为0～1，该值越高表明所含裂隙越多，其中法向裂隙弱度ΔN可表示为［18］

图3中给出了背景层孔隙度变化对垂直裂隙传播纵波速度及逆品质因子的影响，其中，①层孔隙 介 质 的 渗 透 率 κ1＝0.1μm2，粘 度 η1＝1g／（m·s－1），孔隙流体体积模量Kf＝2.25GPa，流体密度ρf＝1g／cm3。对于给定的裂隙弱度ΔN＝0.2，随背景层孔隙度从0.1%变至1.0%时纵波速度频散和衰减表现出迅速的增加，当背景层孔隙度在1%～10%时速度频散和衰减特征差异很小，而当孔隙度大于10%时纵波速度频散和衰减又明显减小，所给出的裂隙孔隙介质在背景孔隙度为1%～10%时具有最强的速度频散和衰减。当背景层的孔隙度接近零值时仅能容纳很少量的从裂隙层中排除出的流体，孔隙流体流动相对较弱而处于非弛豫状态，此时介质的速度频散及衰减均会表现的较小；当背景层的孔隙度增高时能容纳的孔隙流体量也在增加，因此介质的速度频散及衰减会表现出随孔隙度增大的特征；但裂隙层中所排出的孔隙流体的多少取决于背景层与裂隙层的孔隙压力差异，孔隙度增大时弹性波所形成的孔压是减少的，而同时由于裂隙的弱度为定值，因此孔隙压差也会随背景层的孔隙度增大而减少。正是背景层孔隙度变化时存在上述两种作用，使得介质在孔隙度为1%～10%时具有最强的速度频散和衰减。

图4中给出了裂隙弱度变化时对垂直于裂隙传播纵波速度及逆品质因子的影响。在给定背景层孔隙度为20%的情况下，裂隙弱度越高则表明其抵抗外加压力的作用越弱，也即在相同的弹性波作用下所诱发的孔隙压力越大，因此孔压差随裂隙弱度的增加而增大，会造成更多的孔隙流体从裂隙流入背景孔隙介质中，使得介质中传播纵波的速度频散及逆品质因子均会随裂隙弱度的增大而增大。

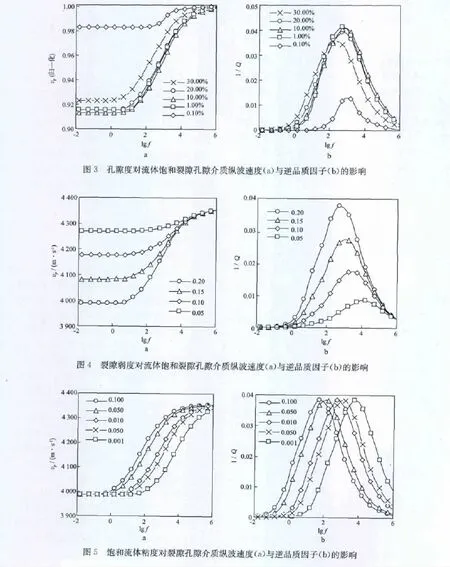
图6 背景层渗透率变化对裂隙孔隙介质纵波速度（a）与逆品质因子（b）的影响

图5与图6中分别给出孔隙流体粘度及背景孔隙介质渗透率变化对垂直于裂隙传播纵波速度及逆品质因子的影响。在裂隙弱度ΔN及孔隙度一定的情况下，弹性波作用下所形成的孔隙压力是一定的，即在裂隙层与背景层的分界面处所形成的孔隙压差一定，该孔压梯度下形成裂隙层与背景孔隙层之间的流体流动以使界面处孔隙压力平衡。那么孔隙流体的粘度越高或者介质渗透率越低则流体流动越不易发生，孔压平衡所需要时间也越长，则需要传播纵波的频率较低以使孔压能在波传播的半周期内平衡。表现出随渗透率的降低以及孔隙流体粘度的增加特征频率（衰减峰值）频率向低频移动，而渗透率与孔隙流体粘度的变化对纵波频散值以及逆品质因子值并无影响，这与传统的Biot理论相异而和喷射流作用类似。

5 结束语

干燥裂隙孔隙介质的等效弹性性质具有横向各项同性介质特征并与线性滑动裂隙模型一致。当纵波通过含流体裂隙孔隙介质时，介质的不同部分由于孔压不均引起孔隙流体在介观尺度上的流动，表现为慢纵波流体扩散作用。裂隙孔隙介质中传播纵波的速度频散及逆品质因子值依赖于背景介质的孔隙度及裂隙弱度ΔN，均会随裂隙弱度的增大而增大；饱和流体粘度以及介质渗透率的变化不改变速度频散或品质因子的大小，但会使特征频率发生移动；特征频率的大小依赖于背景孔隙介质的渗透率与粘度，同时也与裂隙的间隔及密度（裂隙弱度表示）有关。我们导出了含定向裂隙孔隙介质中垂直于裂隙传播纵波的频散方程，它既能有效模拟裂隙对弹性波传播的影响，又同时建立了该类介质速度特征、衰减特征与裂隙特征、裂隙所嵌入的多孔岩石特征、充填流体特征之间的准确关系，可为利用地震及测井资料进行相关裂隙参数的估算提供理论依据，在裂隙、孔隙型油气储层的地震与测井识别方面有一定的应用前景。

［1］Hudson J A.Wave speed attenuation of elastic waves in materials containing cracks［J］.Geophysical Journal of the Royal Astronomical Society，1981，64（1）：133－150

［2］Schoenberg M，Douma J.Elastic wave propagation in media with parallel fractures and aligned cracks［J］.Geophysical Prospecting，1988，36（2）：571－590

［3］Bakulin A，Tsvankin I，Grechka V.Estimation of fracture parameters from reflection seismic data－part I：HTI model due to a single fracture set［J］.Geophysics，2000，65（6）：1788－1802

［4］Dutta N C，Odé H.Attenuation and dispersion of compressional waves in fluid－filled porous rocks with partial gas saturation（White model）－partⅠ：Biot theory，part II：results［J］.Geophysics，1979，44（6）：1777－1805

［5］Norris A N.Low－frequency dispersion and attenuation in partially saturated rocks［J］.Journal of A－coustical Society of America，1993，94（2）：359－369

［6］Brajanovski M，Gurevich B，Schoenberg M.A model for P－wave attenuation and dispersion in a porous medium permeated by aligned fractures［J］.Geophysical Journal International，2005，163（2）：372－384

［7］Ba J，Cao H，Yao P N，et al.Double－porosity rock model and squirt flow in the laboratory frequency band［J］.Applied Geophysics，2008，5（4）：261－276

［8］Yang D H，Zhang Z J.Poroelastic wave equation including the Biot／squirt mechanism and the solid／fluid coupling anisotropy［J］.Wave Motion，2002，35（1）：223－245

［9］邓继新，王尚旭，杜伟.介观尺度孔隙流体流动作用对纵波传播特征的影响研究——以周期性层状孔隙介质为例［J］.地球物理学报，2012，55（8）：2716－2727 Deng J X，Wang S X，Du W.A study of the influence of mesoscopic pore fluid flow on the propagation properties of compressional wave—a case of periodic layered porous media［J］.Chinese Journal of Geophysics（in Chinese），2012，55（8）：2716－2727

［10］Biot M A.Theory of propagation of elastic waves in fluid saturated－porous solid，I：low frequency range，Ⅱ：high frequency range［J］.Journal of the Acoustical Society of America，1956，28（2）：168－191

［11］He T，Zou C，Pei F，et al.Laboratory study on fluid viscosity induced ultrasonic velocity dispersion in reservoir sandstones［J］.Applied Geophysics，2010，7（2）：114－126

［12］Carcione J M.Wave fields in real media wave propagation in anisotropic，anelastic，porous and electromagnetic media［M］.Amsterdam：Elsevier Science，2007：1－538

［13］Müller T B，Rother E.Seismic attenuation due to wave－induced flow：why Q in random structures scales differently［J］.Geophysical Research Letters，2006，33：L16305

［14］Backus G E.Long－wave elastic anisotropy produced by horizontal layering［J］.Journal of Geophysical Research，1962，67（11）：4427－4441

［15］Schoenberg M，Sayers C M.Seismic anisotropy of fractured rock［J］.Geophysics，1994，60（6）：1777－1805

［16］Krief M，Garat J J，Stellingwerff J，et al.A petrophysical interpretation using the velocities of P and S waves （full－waveform sonic）［J］.Log Analyst，1990，31（1）：355－369

［17］Mavko G，Mukerji T，Dvorkin J.The rock physics handbook：tools for seismic analysis of porous media［M］.New York：Cambridge University Press，2009：370－376

［18］Lambert G，Gurevich B，Brajanovski M.Attenuation and dispersion of P－waves in porous rocks with planar fractures：comparison of theory and numerical simulations［J］.Geophysics，2006，71（1）：N41－N45