一种优化组合的GM(1,N)模型

苏海军，邵 艺

(西华师范大学 数学与信息学院，四川 南充 637009)

一种优化组合的GM(1,N)模型

苏海军，邵 艺

(西华师范大学 数学与信息学院，四川 南充 637009)

针对GM(1,N)模型在模拟与预测方面的不足，提出了GM(1,N)模型的一种优化组合方式.第一步是在原GM(1,N)模型灰微分方程上添加一个扰动因素，然后利用优化的背景值确定相应的新参数；第二步利用“最小二乘法”得到模型白化方程近似解中新的初始条件，进而得到一种新的GM(1,N)模型的模拟表达式.实例验证表明，新GM(1,N)模型的适用范围明显拓宽，而且模拟和预测精度均大大提高.

GM(1,N)；优化；预测

0 引言

由邓聚龙教授提出的GM(1,N)模型是灰色系统理论中的重要内容.[1]GM(1,N)模型的建模思路主要分为三步：第一步是确定GM(1,N)灰微分方程的相关参数，第二步是将第一步算出的参数代入白化方程得到GM(1,N)模型的模拟表达式(近似时间响应式)，第三步则是利用累减还原得到序列的模拟值.[2]但在实际建模过程中，往往存在扰动因素，所以本文首先给原灰微分方程添加一个扰动因素项.另外，建模第一步计算出的参数的合理性与背景值选取有直接关系，但现有GM(1,N)模型背景值均采用紧邻均值，不能客观反映系统特征数据序列的发展态势.[3]同时，在第二步的模拟表达式中，选取序列第一个值作为初始条件也缺乏依据.[4]针对上述不足，本文将优化的背景值和利用最小二乘法得到的初始条件同时作用于GM(1,N)模型，得到优化的模拟表达式.经过对数据的模拟和预测发现，本文优化组合的GM(1，N)模型明显优于原模型.

1 基本概念

定义1xj(0)(k)+ajzj(1)(k)=bj1x1(1)(k)+…+bj,j-1xj-1(1)(k)+bj,j+1(1)(k)+…+bjNxN(1)(k)称为GM(1,N)模型，

定理1 设Xj(0)为系统特征数据序列，Xi(0)(i=1,…,j-1,j+1,…,N)为相关因素数据序列，Xi(1)为诸Xi(0)的1-AGO序列，Zj(1)为Xj(1)的紧邻均值生成序列，

定理2 设Xj(0)，Xj(1)(j=1,2,…,N),Zj(1)(j=1,…,N)如定理1所述，则GM(1,N)模型的近似时间响应式(模拟表达式)为

2 优化的GM(1,N)模型

证明:(Ⅰ)

由于zj(1)(k)=λjxj(1)(k-1)+(1-λj)xj(1)(k)，

xj(1)(k)=xj(1)(k-1)+xj(0)(k)，

于是有：

xj(0)(k)+aj[xj(1)(k-1)+(1-λj)xj(0)(k)]

即 [1+(1-λj)aj]xj(0)(k)=

所以

则有

(1)

于是有

(2)

联立(1)，(2)得：

定理4xi(0)(k)+ajzj(1)(k)=bj1x1(1)(k)+

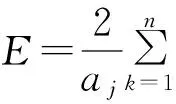
证明:令F(cj)=

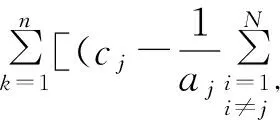
再令F′(cj)=0，有

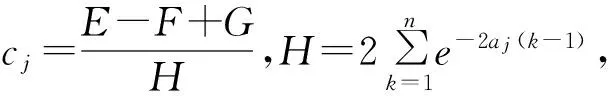
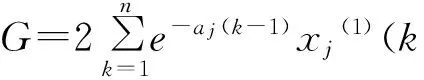
3 数据模拟与预测精度比较

取标准指数序列xi(0)(k+1)=e-ak(k=0,1,2,3,4),分别取-a=0.1，0.3，0.5.

(1)原始序列值：

x1(0)=(1，1.1052，1.2214，1.3499，1.4918),

x2(0)=(1，1.3499，1.8221，2.4596，3.3201),

x3(0)=(1，1.6487，2.7183，4.4817，7.3891).

(2)模拟与预测式：

模型Ⅰ(原GM(1,N)模型)：

模型Ⅱ(本文优化组合的GM(1,N)模型)：

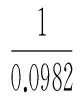
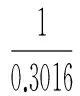
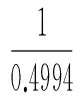
预测公式(预测公式见文献[5])：

模型Ⅰ(原GM(1，N)模型)：

模型Ⅱ(本文优化组合的GM(1，N)模型)：

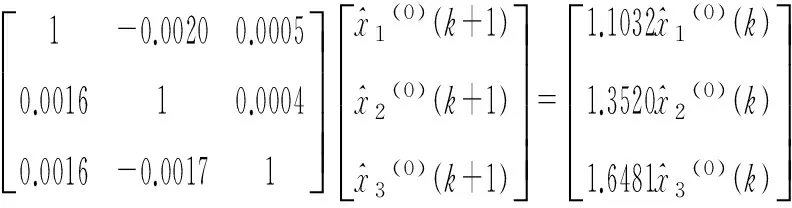
(3)模拟与预测精度比较(结果见表1，表2)

表1 模拟精度比较

表2 预测精度比较

说明：由于表1中的模型Ⅰ无法合理地对变化较急剧的序列X3(0)进行模拟，导致整个系统无法正常预测，因此表2中没有模型Ⅰ的预测值.

从本例的结果可以看出，当数据变化非常平缓时，原模型可以进行有效的模拟，但当数据变化较急剧时，原模型迅速失去其实用性，因此，当系统中一旦出现变化较急剧的数据序列，将严重影响整个系统的预测.而本文优化组合后的模型Ⅱ能在系统出现变化较急剧的数据序列时对系统各数据序列进行有效的模拟和预测，并能够保持较高的模拟和预测精度.

4 结束语

本文针对原GM(1，N)模型只能应用于变化非常平缓的系统数据这一不足，首先在灰微分方程后添加扰动因素项，然后，进一步将优化的背景值和初始条件应用于GM(1，N)模型，通过实例验证发现，经过优化组合的GM(1，N)模型能够保持较高的模拟和预测精度，因此具有重要的应用价值.

[1] 邓聚龙.灰预测与灰决策[M].武汉：华中科技大学出版社，2002:48-51.

[2] 刘思峰，党耀国，方志耕.灰色系统理论及其应用[M].北京：科学出版社，2004:186.

[3] 穆 勇，李 放.灰色优化模型[J].济南大学学报，2001(4)：341-343.

[4] 王义闹，李应川.一种逐步优化灰导数背景值的建模方法[J].系统工程与电子技，2001(7)：76-78.

[5] SHAO Yi,WEI Yong.TheOptimizationofGM(1,N)ModelAndNewMethodofForecasting[J].Journal of Grey System,2009(4):89-94.

[责任编辑邓杰]

OnApproximatingGreyModelGM(1,N)

SU Hai-jun,SHAO Yi

(Mathematics and Information College of China West Normal University, Nanchong Sichuan 637009, China)

In order to make up the defect of GM(1, N), optimizing GM(1, N) model by three steps. The first step is adding disturbance to grey differential equation, using a kind of optimized background value to get new parameters, the second step is using “least squares method” to get the initial value of the solution of white differential equation. Through accumulating example, we can see that the optimized GM(1, N) model has higher simulation and forecasting precision obviously.

GM(1, N);optimization;prediction

2013-02-18

四川省教育厅科研项目“灰色系统模型的优化及数据预处理应用研究”(13ZB0013)

苏海军(1980—)，男，四川广安人.讲师，硕士，主要从事灰色系统理论研究.

O141.4

A

1674-5248(2013)05-0007-04