基于信息熵的河床演变分析

徐国宾，赵丽娜

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

自克劳修斯 1854年提出熵这一概念以来，它已被广泛应用于社会、经济、生态等领域．作为一个状态函数，熵的含义非常丰富：在热力学中，它是不可用能量的量度；在统计物理学中，它是系统微观状态数目多少的量度；在信息论中，它是随机事件不确定性的量度[1]．

根据系统与外界相互作用程度，可将系统分为孤立系统、封闭系统和开放系统．随着热力学理论的发展，热力学分为经典热力学和非平衡态热力学．经典热力学主要研究孤立系统和封闭系统，1865年德国物理学家克劳修斯提出最大熵原理，即在孤立系统中，系统的熵服从最大熵原理．非平衡态热力学主要研究开放系统，对于河流系统这样的开放系统，系统应该服从最小熵产生原理．早期，经典热力学中孤立系统的熵在河流动力学领域得到广泛应用，Leopold等[2]根据孤立系统的熵，提出河流能量沿程均匀分布的最大统计熵理论；Yang[3]将河流系统与热力学系统进行对比，推导出最小能耗率理论；黄万里[4]根据热力学第二定律，提出最大能量耗散率理论；陈绪坚等[5]从能量和或然率的角度研究河流能量耗散和分配的规律，提出河流熵理论．徐国宾等[6]指出，上述学者采用最大熵原理在此领域中应用存在的具体问题，但是他们做出的贡献仍然不可磨灭．徐国宾等[7-8]在前人研究的基础上，基于非平衡态热力学的基本理论，推导出最小熵产生等价于最小能耗率．迄今为止，基于熵理论的河床演变研究多限于对现象的定性描述，较少提出定量的计算．本文对影响河床演变的各个因素进行分析，得出各个因素的客观权重，定量计算河段年份信息熵，并结合实际情况对计算结果进行验证．

1 信息熵的基本概念

熵是热力学中的一个基本概念[9]，用来表示系统的一个状态函数，一般用符号S表示．1948年，Shannon首次将熵的概念引入信息论，称其为信息熵，用以表示系统的不确定性、稳定程度和信息量．信息是系统有序程度的一个度量，信息熵是系统无序程度的一个度量，二者绝对值相等，符号相反．对于一个不确定性系统，若用随机变量X表示其状态特征，对于离散型随机变量，设x的取值为，每一取值对应的概率，且有

本文将信息熵分为两类：一类是指标信息熵，另一类是年份信息熵．指标信息熵是指同一个影响因素在若干年内对系统的效用值，效用值越高，其重要性越大；年份信息熵是表示系统在一年中所有影响因素产生的子熵加权和．

2 用熵值法确定影响因素的权重

影响冲积河流河床演变的外界因素主要有来水来沙条件和河床边界条件[10-11]．本文主要研究来水来沙条件(包括流量、含沙量、沉速)和河床边界条件，如比降、糙率、宽深比等影响因素对系统引起的子熵及其权重．

由于各个影响因素对河床演变的影响程度有一定差别，因此有必要对各个影响因素对河床演变的权重做定量计算．在信息论中，信息熵反映了信息无序化程度，信息熵越小，系统无序度越小，信息的效用值越大；信息熵越大，系统的无序度越高，其信息的效用值越小．对于n年m个影响因素的初始矩阵，可以利用熵值法计算各影响因素的权重[12-13]．其计算步骤如下所述．

(1) 构建n年m个影响因素的初始矩阵Xi×j=

(2) 影响因素的归一化处理．

由于各个因素所表征对象的量纲和数量级大小都不相同，因此为了排除由于量纲及数量级大小不同造成的影响，需要对原始数据进行归一化处理．将河段的影响因素进行归一化，归一化计算式为

式中：xi∗j为经过归一化后的值；xij为第i年第j个影响因子的实测值；xj,max和xj,min分别为第j个影响因子所有年中的最大值和最小值．

(3) 计算指标信息熵S．j

式中：Sj为第j个影响因素的信息熵；xj为第j个影响因素所有年之和．

(4) 计算影响因素的熵权重jλ．

式中jλ为第j个影响因素引起的子熵权重．

3 年份信息熵计算

由于各个影响因素对河床演变的影响程度有一定差别，因此河流系统的年份信息熵是系统在一年中所有影响因素产生的子熵的加权和，其计算式为

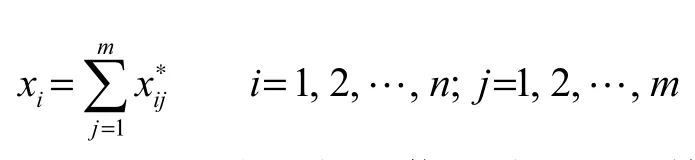
式中：S为河流系统的年份信息熵；Sij为第i年第 j个影响因素引起的河流年份信息子熵；xi为第i年所有影响因素之和．

4 应用实例

根据黄河下游花园口、夹河滩、高村、孙口、艾山、泺口和利津7个水文站的1972年、1973年、1975年、1976年、1978—1980年、1982年、1985年、1987年、1988年、1991—1996年和 1998—2000年水文年鉴及黄河水利委员会实测资料[14]，选取流量、含沙量、沉速、比降、糙率和宽深比 6个影响因素表示河流的状态特征，如表 1～表 6所示，用来计算各个影响因素对河床演变影响的权重和各个河段的年份信息熵．

表1 花—夹河段影响因素的实测值Tab.1 Values of influencing factors of Hua—Jia reach

表2 夹—高河段影响因素的实测值Tab.2 Values of influencing factors of Jia—Gao reach

表3 高—孙河段影响因素的实测值Tab.3 Values of influencing factors of Gao—Sun reach

表4 孙—艾河段影响因素的实测值Tab.4 Values of influencing factors of Sun—Ai reach

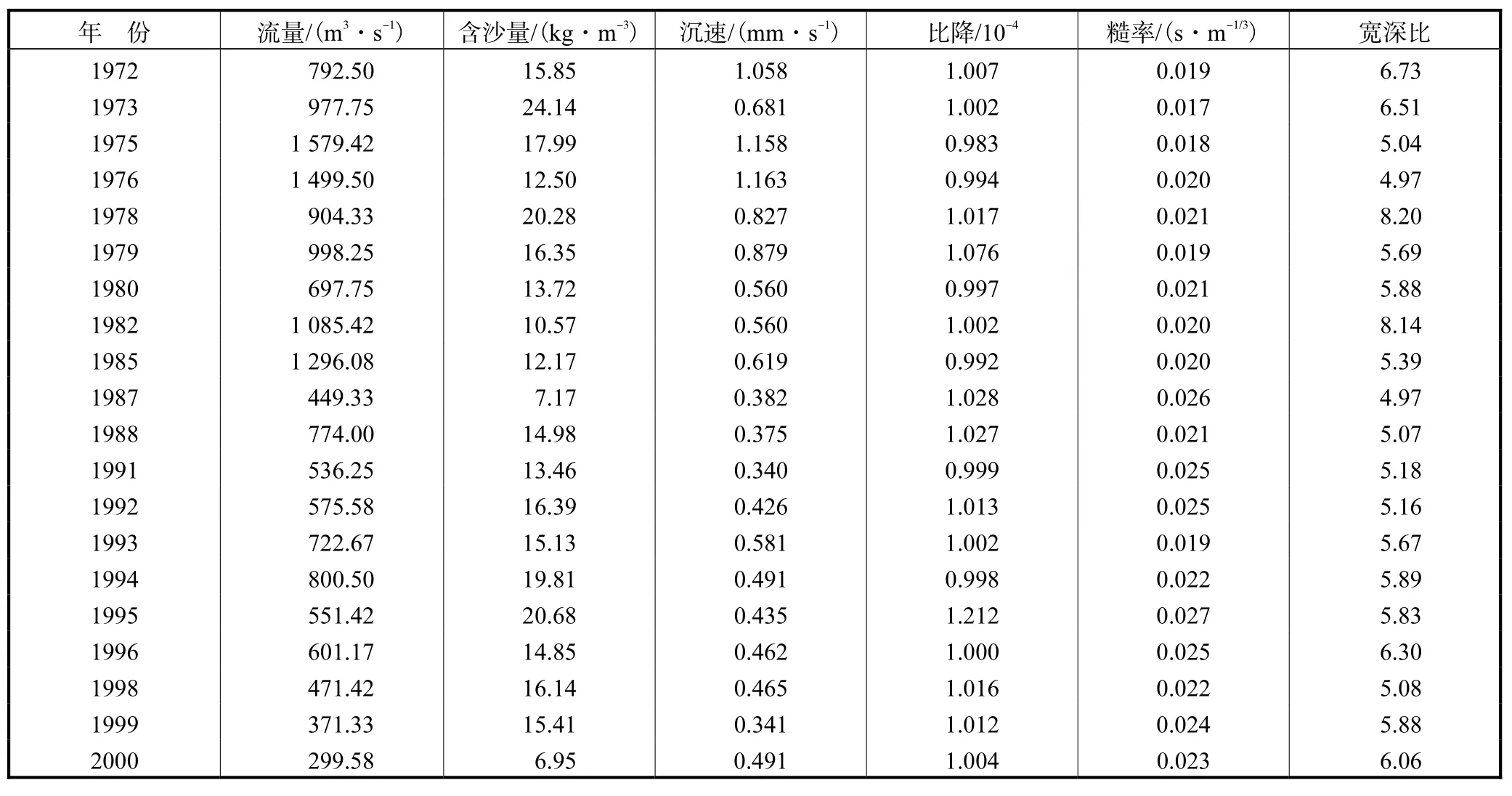
表5 艾—泺河段影响因素的实测值Tab.5 Values of influencing factors of Ai—Luo reach

表6 泺—利河段影响因素的实测值Tab.6 Values of influencing factors of Luo—Li reach

用熵值法计算各个影响因素对河床演变影响的权重，根据式(1)和式(2)计算得出流量、含沙量、沉速、比降、糙率和宽深比各影响因素的指标信息熵，指标信息熵的大小代表了 1个影响因素在若干年内对系统的效用值，指标信息熵越小，影响因素效用值越高，则其重要性越大；反之，指标信息熵越大，影响因素效用值越低，则其重要性越小．根据式(3)计算得出流量、含沙量、沉速、比降、糙率和宽深比的权重jλ=(0.135，0.104，0.188，0.184，0.060，0.329)．根据式(4)和式(5)计算河流系统的年份信息熵，即影响因素引起的河流年份信息子熵加权和，6个河段 20年的河流年份信息熵如图1所示．

由权重jλ的值可以看出，反映组成河岸与河床物质的相对可动性的宽深比对河床演变的权重最大，代表河床边界条件的比降、糙率和宽深比的权重总和为 0.573，代表来水来沙条件的流量、含沙量和沉速的权重总和为 0.427，因此可以认为河床边界条件对河床演变的影响大于来水来沙条件．

20世纪 70年代众多学者重点研究了不同地区来水来沙对黄河下游河道冲淤的影响，取得了突破性进展，明确了粗泥沙来源区的泥沙对黄河下游河道的危害最为严重，对黄河治理起到了重大指导作用[15].本文通过定量计算河床边界条件和来水来沙对河床演变的影响程度，得出了河床边界的控导工程对黄河河道治理更加重要的结论．

图1 6个河段20年信息熵变化Fig.1 Information entropy of 6 reaches in the range of 20 years

由图1可以看出，6个河段的年份信息熵的大小依次是花—夹河段、夹—高河段、高—孙河段、孙—艾河段、艾—泺河段和泺—利河段．信息熵是系统无序程度的一个度量，因此可以得出6个河段的无序程度大小依次是花—夹河段、夹—高河段、高—孙河段、孙—艾河段、艾—泺河段和泺—利河段，该计算结果与实际情况相符，花—夹河段和夹—高河段是典型的游荡河段，其特点是散乱；艾—泺河段和泺—利河段是典型的弯曲河段，其特点是有序稳定；高—孙河段和孙—艾河段是介于游荡河段与弯曲河段之间的过渡河段，其特点也是介于两者之间．

20世纪70年代以来，由于河道整治工程的建设，使陶城铺以下河段(艾—泺河段和泺—利河段)已经形成控制较好的弯曲型河道，高村至陶城铺过渡型河段(高—孙河段和孙—艾河段)的河势也基本得到控制，高村以上游荡型河段(花—夹河段和夹—高河段)布设了一部分控导护滩工程[16]．总体看来，河防工程的建设使河段的信息熵不会再有增大趋势．另外，通过修建一些控导护滩工程，游荡型河段的宽、浅、乱状态有所改善，主流趋于单一，摆动范围减小，致使花—夹河段和夹—高河段的信息熵具有减少趋势．

5 结 论

(1) 采用熵值法确定了不同影响因素对河床演变的影响权重，由权重值的大小可以看出能够反映组成河岸与河床物质的相对可动性的宽深比对河床演变的权重最大，河床边界条件对河床演变的影响大于来水来沙条件．

(2) 计算了6个河段各 20年的年份信息熵，通过对比得出 6个河段的年份信息熵的大小，依次是花—夹河段、夹—高河段、高—孙河段、孙—艾河段、艾—泺河段和泺—利河段，定量验证了信息熵越大系统越混乱、信息熵越小系统越有序的结论．

(3) 花—夹河段和夹—高河段游荡型河段的信息熵具有减少趋势，说明该游荡河段的游荡程度有所下降．

［1］ 任鲁川. 灾害熵：概念引入及应用案例[J]. 自然灾害学报，2000，9(2)：26-31.Ren Luchuan. Disaster entropy：Conception and application[J].Journal of Natural Disasters，2000，9(2)：26-31(in Chinese).

［2］ Leopold L B，Langbein W B. The Concept of Entropy in Landscape Evolution[EB/OL]. http://pubs.usgs.gov/pp/0500a/report.pdf，2012-11-26.

［3］ Yang C T. Potential energy and stream morphology[J].Water Resources Research，1971，7(2)：311-322.

［4］ 黄万里. 水动力——热动力学的极值定律[J]. 应用数学和力学，1983(4)：469-476.Huang Wanli. The extremity laws of hydrothermodynamics[J].Applied Mathematics and Mechanics，1983(4)：469-476(in Chinese).

［5］ 陈绪坚，胡春宏. 河流最小可用能耗率原理和统计熵理论研究[J]. 泥沙研究，2004(6)：10-15.Chen Xujian，Hu Chunhong. Research on the theory of minimum rate of available energy dissipation and statistic entropy in rivers[J].Journal of Sediment Research，2004(6)：10-15(in Chinese).

［6］ 徐国宾，练继建. 河流调整中的熵、熵产生和能耗率的变化[J]. 水科学进展，2004，15(1)：1-5.Xu Guobin，Lian Jijian. Changes of the entropy production and the rate of energy dissipation in river adjustment[J].Advances in Water Science，2004，15(1)：1-5(in Chinese).

［7］ 徐国宾，练继建. 流体最小熵产生原理与最小能耗率原理(Ⅰ)[J]. 水利学报，2003，34(5)：35-40.Xu Guobin，Lian Jijian. Theories of the minimum rate of energy dissipation and the minimum entropy production of flow(Ⅰ)[J].Journal of Hydraulic Engineering，2003，34(5)：35-40(in Chinese).

［8］ 徐国宾，练继建. 流体最小熵产生原理与最小能耗率原理(Ⅱ)[J]. 水利学报，2003，34(6)：43-47.Xu Guobin，Lian Jijian. Theories of the minimum rate of energy dissipation and the minimum entropy production of flow(Ⅱ)[J].Journal of Hydraulic Engineering，2003，34(6)：43-47(in Chinese).

［9］ 龚茂枝. 热力学[M]. 武汉：武汉大学出版社，1998.Gong Maozhi.Thermodynamics[M]. Wuhan：Wuhan University Press，1998(in Chinese).

［10］ 徐国宾，杨志达. 基于最小熵产生与耗散结构和混沌理论的河床演变分析[J]. 水利学报，2012，43(8)：948-956.Xu Guobin，Yang Chih Ted. Analysis of river bed changes based on the theories of minimum entropy production dissipative structure and chaos[J].Journal of Hydraulic Engineering，2012，43(8)：948-956(in Chinese).

［11］ 徐国宾. 河工学[M]. 北京：中国科学技术出版社，2011.Xu Guobin.River Engineering[M]. Beijing：China Science and Technology Press，2011(in Chinese).

［12］ 李 淼，夏 军，李福林，等. 基于熵权的属性识别模型在海水入侵现状评价中的应用[J]. 地理科学进展，2012，31(3)：324-329.Li Miao，Xia Jun，Li Fulin，et al. The application of attribute recognition model based on coefficient of entropy to the assessment of seawater intrusion[J].Progress in Geography，2012，31(3)：324-329(in Chinese).

［13］ Zhang Hong，Gu Chaolin，Gu Luwen，et al. Case study the evaluation of tourism destination competitiveness by OPSIS and information entropy—A case in the Yangtze River Delta of China[J].Tourism Management，2011，32：443-451.

［14］ 史传文. 河型模糊控制基础[M]. 郑州：黄河水利出版社，2009.Shi Chuanwen.Based on Fuzzy Control Method on the River Patterns[M]. Zhengzhou：Yellow River Water Conservancy Press，2009(in Chinese).

［15］ 赵业安，周文浩，费祥俊，等. 黄河下游河道演变基本规律[M]. 郑州：黄河水利出版社，1998.Zhao Ye′an，Zhou Wenhao，Fei Xiangjun，et al.The Basic Law of the Fluvial Process in the Lower Yellow River[M]. Zhengzhou：Yellow River Water Conservancy Press，1998(in Chinese).

［16］ 胡一三，张红武，刘贵芝，等. 黄河下游游荡性河段河道整治[M]. 郑州：黄河水利出版社，1998.Hu Yisan，Zhang Hongwu，Liu Guizhi，et al.River Training in the Wandering Reach in the Lower Yellow River[M]. Zhengzhou：Yellow River Water Conservancy Press，1998(in Chinese)．