基于时间序列方法的网络信号传输时延预测

郭诗朦，张严心，朱 淑

（北京交通大学 电子信息工程学院，北京 100044）

随着铁路信息化的逐步完善，网络化的信号传输变得越来越普及,网络化控制系统（NCS）在铁路控制信号的发送和接收过程中起着重要作用，网络控制系统是通过网络形成的反馈控制系统，这种控制模式具有资源共享、连线少、易扩展、易维护，高效率、高可靠性及高灵活性等优点，是未来控制系统的发展模式。但是由于网络的介入和传输距离的扩大，资源竞争网络拥塞等现象不可避免地造成数据传输时延，从而导致系统性能变差，甚至影响系统稳定性[1]。所以，对时延的准确估计可以有效提高控制算法的准确性、实时性和鲁棒性。文献[2]采用AR模型对时延进行在线估计，从而减小计算量，提高算法的实时性。但使用AR模型是一种被动的“黑盒子”方法，仅依据原始数据对模型不断逼近，而忽略了系统的先验信息产生的数据。从控制工程观点来看，状态空间模型较AR模型有更多的结构优点，但因网络的复杂性，可用来建模的状态量很少[3]。权衡两种方法的利弊，本文提出一种基于状态空间的时间序列分析方法，对时延进行有效的预测。首先对时延序列建立合适的ARMA模型，然后转换为状态空间模型表述，从而使预测更加准确，并使控制算法更有效率，根据时延的确定控制算法改变传输的信号来补偿网路时延，可以较好地提高控制的实时性和控制效果。

1 时间序列预测的状态空间算法

状态空间模型求解算法的核心是Kalman滤波，Kalman滤波是在时刻t基于所有可得到的信息计算状态向量的最理想的递推过程。当扰动项和初始状态向量服从正态分布时，Kalman滤波能够通过预测误差分解计算似然函数，从而可以对模型中的所有未知参数进行估计，并且当新的观测值一旦得到，就可以利用Kalman滤波连续地修正状态向量的估计。

1.1 时间序列的状态空间表述

1.1.1 ARMA模型的建立

ARMA模型的一般形式为：

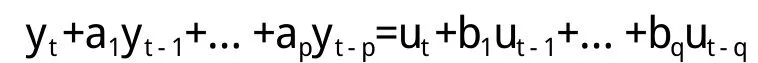
用Bk表示k步线性推移算子，即Bkyt=yt-k,BkUt=Ut-k, Bkc≡c，c为常数。并令bn：

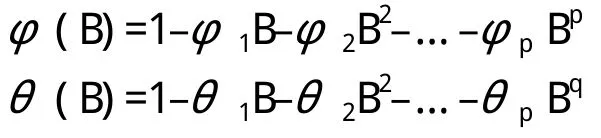
则可简记为：

这一模型称作p阶自回归-q阶滑动平均混合模型，记为ARMA(p, q)模型。

1.1.2 转换为状态空间模型

考虑如下ARMA模型系统：

yt+a1yt-1+…+apyt-p=b0ut+b1ut-1+…+bqut-q

其中，Ut为稳定的白噪声。

令 ap+1=ap+2=…=am=0，bq+1=bq+2=…=bm=0

其中，m=max{p，q}。从而利用状态空间标准型的转换方法，得到此ARMA系统状态空间描述的可观标准型为：

yt=[1 0 0…0]xt+b0ut

可控标准型为：

yt=[b1_a1b0b2_a2b0…bm_amb0]xt+b0ut

其中，若令b1=b2=…=bm=0，可得到AR系统模型的状态空间表述，反之令a1=a2=…=am=0，可得到MA系统模型的状态空间表述。

1.2 Kalman滤波估计

状态空间建模中，初期的目标是在有噪声的环境下估计信号值，即状态量xt，要解决此类问题，Kalman滤波是一个简单有效的方法。Kalman滤波过程分为预测和更新两个阶段，这样的方法允许当一个新的观测数据到来时，对状态xt的估计值进行更新，以保证预测数据的时效性。

状态空间模型可写为：

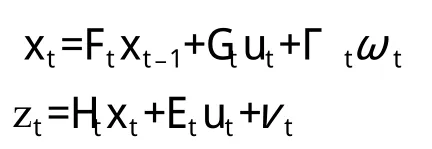
两式分别为系统的状态方程和观测方程，其中：Ft(nx×nx)为传递阵, Gt(nx×nu)为输入增益阵，Ht(nz×nx)为输出阵，Et(nz×nu)为输入-输出阵，Γt(nx×nω)为噪声增益阵，{vt}和{ωt}为均值为零的向量白噪声，它们相互正交并已知协方差，Σt=E[ωtωt']，Rt=[vtvt']。

考虑以上模型方程，状态x的最小均方差估计可以通过以下式子逐步算出：

预测：

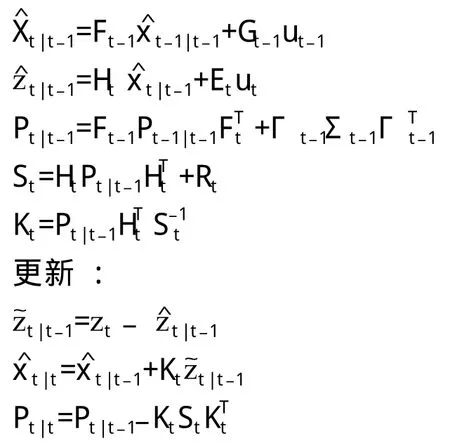
通过以上的递归算法，可以使当前的估计值始终基于全部过去时刻的测量值，并且不需要一个不断扩展的记忆空间，也从另一个方面减小了计算量。卡尔曼滤波方法的另外一个优点是当系统有一个潜在的模型时，可以很快收敛，并且可以跟踪随时间变化而变化的模型。

2 仿真实例

时延预估仿真如下：

在实验室环境下使用Matlab进行仿真，数据采取实验室到Google的RTT值，使用Pingtester软件进行测量，每分钟发送一次32 byte的数据包，并记录返回时间，得到该数据包传输的RTT值，截取其中的一段数据，每隔10个值采样一次，共取500组数据，以达到良好的时延变化趋势，用数据的前半部分进行建模，后半部分进行算法验证，使用Matlab对数据进行ARMA模型建模并建立状态空间模型，然后通过Kalman滤波方法给出预报值，用预报值与实际值对比，得到曲线如图1所示。

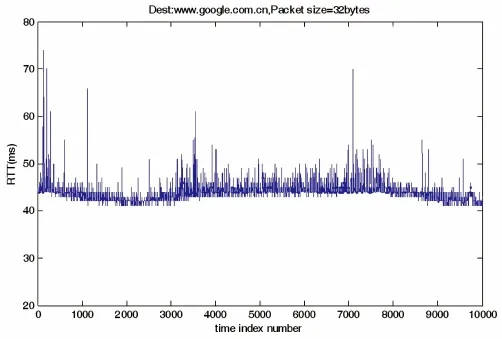
图1 测得时延值

图1 为通过软件测得的实际延时值，延时趋势呈现较为稳定的走向，在信号传输过程中会受到这些延时的影响，从图2可以看出，通过算法求得的预测曲线与实际的曲线趋势基本一致，表明该方法可以准确地对时延进行预测。

图2 时延预测轨迹

3 结束语

本文针对铁路信号的网络传输时延问题，提出了一种新型的延时预测方法,利用已测数据建立ARMA模型并转化为状态空间模型，通过Kalman滤波方法对未来的时延值进行估测，最后通过仿真验证了时延估测的准确性和实时性。该算法减小了控制过程的计算量，但对大量丢包的情况容易造成系统的不稳定，在今后值得进一步研究。

[1]岳 东，彭 晨，Qinglong Han.网络控制系统的分析与综合[M]. 北京：科学出版社，2007.

[2]时维国，邵 诚，孙正阳.基于AR模型时延预测的改进GPC网络控制算法[J].控制与决策，2012，27 ( 3).

[3]Ming Yang X. Rong Li. Predicting End-to-End Delay of the Internet Using Time Series Analysis[J]. Nov. 11, 2003.

[4]陈 虹，严法高，史旺旺. 网络控制系统中考虑动态延时的广义预测控制算法[J]. 信息与控制，2008, 37（2）：224-227.

[5]王 伟. 广义预测控制理论及其应用[M]. 北京：科学出版社，1998：28-34.

[6]梁晓明，刘福才，王 娟. 基于状态空间模型的广义预测控制快速算法[J].计算机仿真, 2009, 26（4）.

[7]Rudy Negenborn. Robot Localization and Kalman Filters On finding your position in a noisy world[M]. 2003.

[8]邓自立.卡尔曼滤波与维纳滤波—现代时间序列分析方法[M].哈尔滨：哈尔滨工业大学出版社，2001.

[9]X. Rong Li, Yunmin Zhu, Jie Wang, and Chongzhao Han.Optimal Linear Estimation Fusion—Part I: Unified Fusion Rules[J]. IEEE TRANSACTIONS ON INFORMATION THEORY，2003，49（9）.

[10]KunjieLi, G.P.Liu. A Simplified GPC Algorithm of Networked Control Systems[J]. Proceedings of the 2007 IEEE International Conference on Networking, Sensing and Control,London, UK, 2007.4.

[11]Wenshan Hu, G.P.Liu, David Rees. Networked Predictive Control Over the Internet Using Round-Trip Delay Measurement[J]. IEEE TRANSACTIONS ON INSTRUMENTATION AND MEASUREMENT, 2008, 57(10).

[12]Wenshan Hu, G. P. Liu, David Rees. Design and Implementation of Networked Predictive Control Systems Based on Round Trip Time Delay Measurement[J]. Proceedings of the 2006 American Control Conference Minneapolis, Minnesota,USA, June 14-16, 2006.

[13]王天堃，周黎辉， 韩 璞，徐大平. 网络化控制系统传输时延与丢包补偿[C]. Proceedings of the 26th Chinese Control Conference , Zhangjiajie, Hunan, China. 2007.

[14]韩路跃，杜行检. 基于MATLAB的时间序列建模与预测[J]. 计算机仿真，2005（4）.

[15]X. R. Li. Applied Estimation and Filtering[D]. University of New Orleans, New Orleans, LA, 2002.