改进的灰色模型在高速铁路沉降观测中的应用

边庆友 李夕明 陈宇扬

（1.宿州市土地勘测规划设计院 安徽 宿州 234000）

引言

为保证高速列车安全运行，要求列车运行轨道具有高度的平顺性，以确保高速列车运行的安全性及舒适性。相对于普通铁路而言，高铁对轨道的要求高得多，轨道的平顺性控制在毫米级，这就要严格对轨道下的构筑物做好设计和施工。我国幅员辽阔，地质条件复杂多样，因此控制不同构筑物的沉降是高铁修建的重中之重，高速铁路速度达300km/h 以上，相对于普通铁路的速度增加了许多，旅客对于速度的提高所带来的舒适度的要求也更高，因此，沉降监测是高铁技术的关键之一。

通常情况下，高铁线路的地基的稳定性及控制地基的强度的处理，都是相对较容易的，不是构成沉降的主要因素。而高铁的线下构筑物的沉降是设计和施工过程中相对较难的工作，也是沉降的主要影响因素。因此，在施工过程中实时对路基、桥梁等构筑物的沉降监测，结合沉降观测数据对不同构筑物的沉降趋势进行预测非常重要。所以，高速铁路的沉降预测是控制线下构筑物沉降、轨道稳定性和平顺性、确保高速列车安全运行的重要条件。目前，国内外高速铁路的沉降监测的方法分为两种，第一是根据固结理论通过室内土实验获取土的参数，然后选择相应的模型来计算沉降；第二是根据对实测数据进行处理，获取数据沉降的规律，从而预测沉降。影响高速铁路各种构筑物的沉降因素很多，单纯依靠理论计算预测效果并不理想，因此根据沉降量—时间曲线，结合预测模型获得沉降量预测的方法较为理想，这也对指导施工和保证工程进度提供科学的指导，并且同时对检验工程质量提供技术保障，在工程上得到广泛的应用。目前常用的几种沉降预测模型有规范双曲线法、固结度对数法、指数曲线法、Asaoka 法以及改进双曲线法。加上本篇阐述的灰色GM（1，1）预测方法，以及对灰色GM（1，1）法的光滑度进行改进的静态、动态预测模型。

1 传统的灰色模型

由于传统的静态灰色模型受到原点误差以及预测序列长度的不同的影响，预测结果精度较差。因此，有人提出预测维度不变的动态预测模型，即每次预测时预测序列的长度固定不变，预测结果只有一个，当进行下一次预测时，上次预测的序列中最前面的旧值除去一个，在序列的最后面增加一个新预测的值，这样保持预测序列长度固定不变，一直预测下去。该种方法将会减小原点误差的影响和序列长度的影响，使原始数据序列始终保持最新的状态和最佳的序列长度，因此，预测结果将会有明显的提高。其具体的建模步骤如下[18]：

设有原始数据序列：Y(0)={x(0)(1),x(0)(2),…x(0)(m)}，x(0)(k)≥0。取原始序列Y(0)中前n(n＜m)个数据作为灰色模型的初始预测序列，进行第一次灰色预测，X(0)={x(0)(1),x(0)(2),…x(0)(n)}，k=1,2,…n，利用X(0)数据序列建立GM(1,1)模型，建立模型的步骤和上面第三节相同，再对X(1)进行累减还原（1-IAGO）,得X(0)的预测公式为：

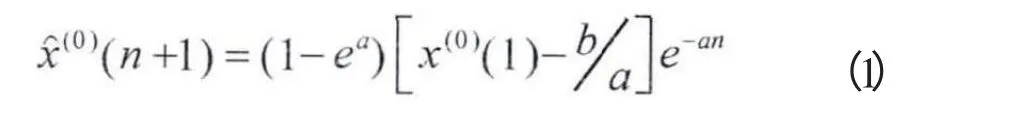
当n+1 小于或等于m时，取序列Y(0)中的部分数值X(0)={x(0)(1),x(0)(2),…x(0)(n+1)}作为初始的预测序列，再次进行预测，得预测值为x(0)(n+2)；当n+1 大于m时，取原始序列值为X(0)={x(0)(2),x(0)(3),…x(0)(n+1)}，得新的预测值x(0)(n+2)。如此递补预测下去，不断更新初始数据序列，直到得到所需的预测值为止。此方法更能体现动态，且切合实际的数据变化，有广泛的适用性。

2 改进的灰色模型

灰色GM(1,1)模型是对原始序列进行累加生成和累减还原的模型，而实际采集的沉降数据受各种客观条件的限制，如果直接应用于模型预测，预测的效果不理想。因此需要对原始序列进行光滑度的处理，提高原始序列的光滑度。经过国内外学者的研究表明，数据的光滑度越高，灰色模型的精度越高。因此，本文使用基于含参二次函数的光滑度提高方法，下面是对改进方法的证明：

设序列X0=[X0(1),X0(2)…，X0(n)][21]，

定理1 设{xi}i=1,2,…，n 为严格单调递增数列，且x1＞0，则，其中p＞0，q≥0，。

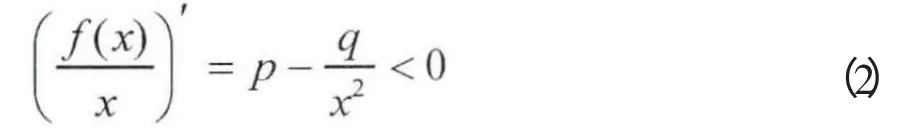
则有，

证毕。

由定理1的证明可以得出：经过二次函数的变换能够提高原始序列的光滑度。

3 京沪高铁某标段沉降变形的灰色模型预测

3.1 工程地质概况及数据选取

本文实验数据选取京沪高铁江苏丹阳至昆山特大桥常州西桥DK1135+667（356#墩）沉降变形观测工作自2008年7月20日起开展，至2010年1月8日架梁完毕，累计进行18个月的观测工作，昆山特大桥设计时速为380km/h，双线轨无砟道，实验工点所在的特大桥主梁形式为32m 简支梁。桥址位于长江冲击平原区，地势平坦，地面高程5m～7m，沿线多为农田、村庄、河流、道路众多，地表水系发育，属长江三角洲河塘相冲击平原地貌。所在地区属于第四系全新统冲击洪积相沉积层。实验地区地下水为第四系孔隙潜水，主要靠大气降水及地表径流补给，水位受季节及气候条件的影响较大，勘测期间测得地下水稳定水位埋深0.30m～3.5m。高速铁路桥梁在整个高铁线路中占的比例最大，为了保证桥梁使用的质量和安全性，就需要了解桥梁墩台的沉降变形特点，务必保证沉降监测有足够的时间。通过大量的沉降监测数据发现，桥梁墩台沉降在桥梁施工的各个阶段有如下规律：

（1）桥梁的沉降随着浇筑的进行，沉降曲线跟随荷载的增加呈线性变化；

（2）架梁期间，架梁车通过荷载突然增加导致沉降量突然增大，沉降出现拐点；

（3）架梁两个月以后沉降量趋于稳定。

3.2 模型算法设计

本文阐述的几种模型算法用MATLAB 实现，下面以某断面的七组数据：时间t时刻t ={0,8,15,23,30,39,47} 对应的沉降值 S ={2.54,3.17,3.63,4.19,4.53,4.98,5.28}为例，对每种算法用MATLAB的设计如下：

1.传统的灰色预测模型建模步骤：

Step1：以此断面数据为例，记X(0)(i)={2.54,3.17,3.63,4.19,4.53,4.98,5.28} 使用该组数据建立起的GM（1,1）模型，利用最小二乘估计。

得

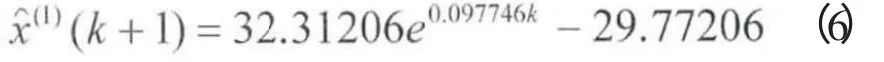
Step2：对X(1)进行累减还原（1-IAGO）,得X(0)的预测公式为：

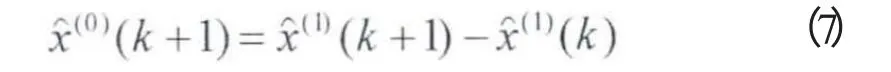
2 改进的灰色预测模型建模步骤：

Step1：对X(0)(i)={2.54,3.17,3.63,4.19,4.53,4.98,5.28}初始数据进行变换，由进行光滑度处理后得到的转化序列为：

Step2：对新生成的数据序列{y(0)(k)}(k=1,2,…，n)作为初始数据序列，使用GM(1,1)模型利用最小二乘估计，代入下式

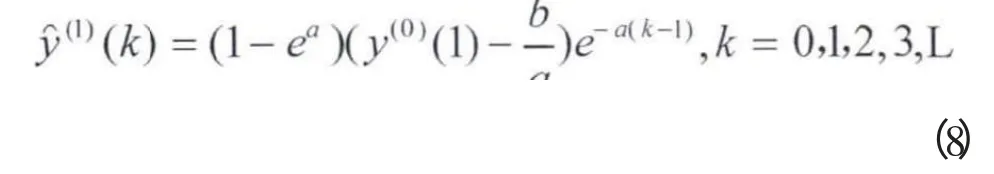
Step3：把预测结果y(0)(k)带入到函数变换式y=ln[p(x(0)(k)2+q)]中，进行一次逆变换处理求出式中的x(0)(k)，具体的含参函数的改进灰色模型预测公式为：

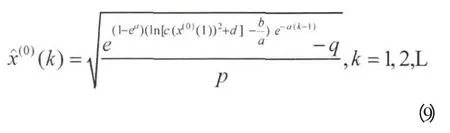
其中：x(0)(1)=x(0)(1)，再对参数p、q的值进行试探选择，获取精度和拟合值较高的预测值。

3.3 模型预测

由图1沉降曲线可以看出，桥梁墩台的沉降量随着荷载的增加而增加，运梁车通过时荷载量突然增加，沉降曲线出现拐点，随着荷载稳定时沉降量逐渐稳定。由于桥梁监测分为两个阶段，在第一阶段数据量较少，架梁产生的突然沉降量过大，对整个阶段的预测产生一定的影响。下面是对桥梁恒载期进行沉降分析，选取DK1135+667D1 实验工点为研究对象，分别采用灰色静态GM（1,1）、灰色静态改进GM（1,1）、灰色动态GM（1,1）（选取9 维数据）、灰色动态改进GM（1,1）模型（选取9 维数据）进行预测研究。在静态改进的预测模型中取参数p=1，q=1800，在动态改进的预测模型中取参数p=1，q=5000，预测结果见上页表1、表2所示。

表1 DK1135+667D1点灰色及改进灰色模型预测结果表

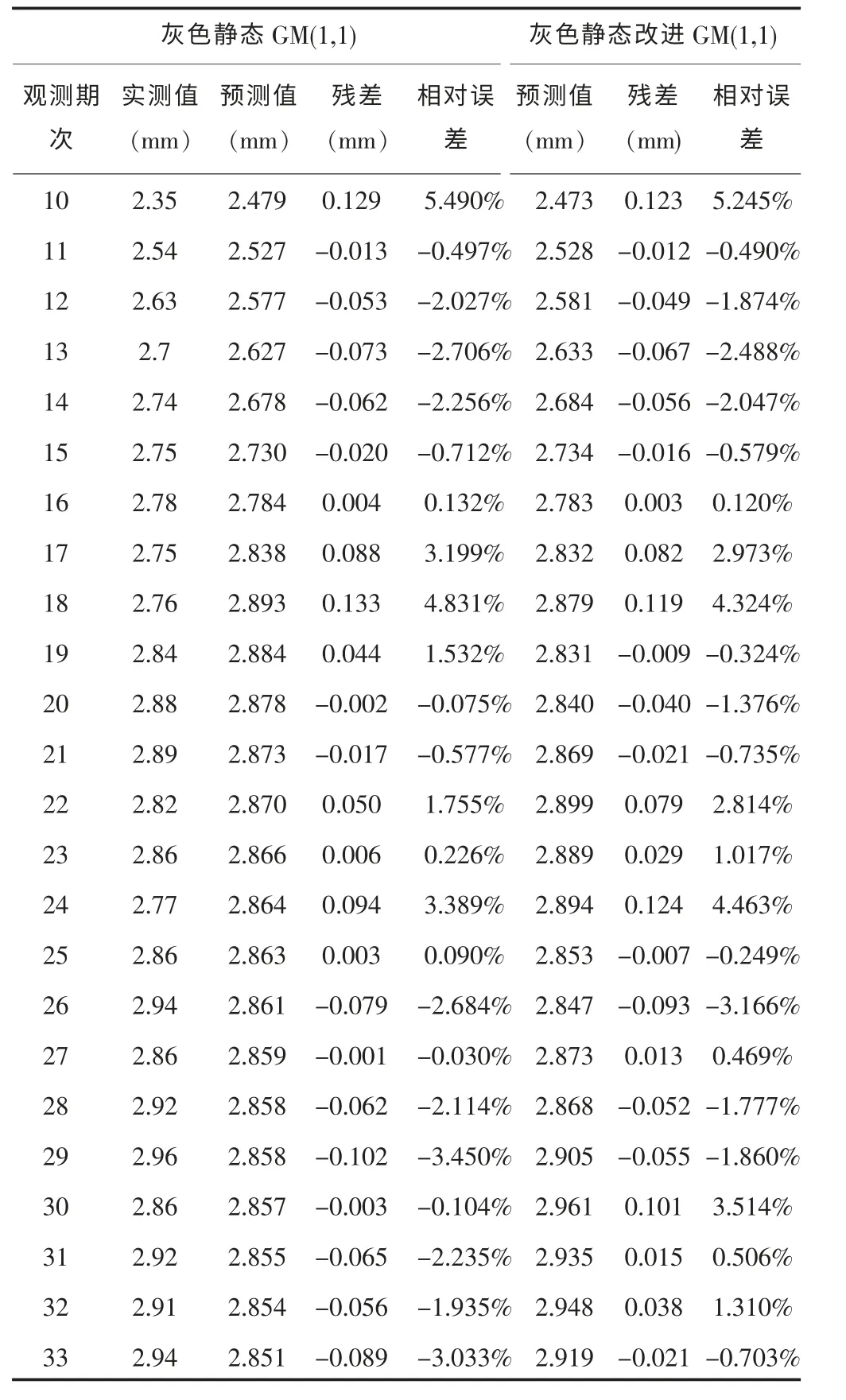
表2 DK1135+667D1点灰色及改进灰色模型预测结果表

由表1、2可以看出，采用灰色静态GM（1,1）预测模型，模型的平均相对误差为2.105%，模型精度为97.895%，后验差比值C= 0.44，小概率误差P=0.96；灰色静态改进GM（1,1）预测模型p=1，q=1800时模型的平均相对误差为2.000%，模型精度为98.000 %，后验差比值C= 0.43，模型的小概率误差P= 0.96。

灰色动态GM（1,1）预测模型，模型的平均相对误差为1.940%，模型精度为98.06 %，后验差比值C=0.51，小概率误差P=0.75；灰色动态改进GM（1,1）预测模型p=1，q=5000时模型的平均相对误差为1.777%，模型精度为98.223 %，后验差比值C=0.36，小概率误差P=1.00。右上图是实测值与灰色模型和本文改进的预测值的对比图。

4 结论与建议

（1）桥梁恒载期，静态灰色模型改进后的预测效果与改进前基本持平，后验差比值和小概率误差概率有所提高。

（2）桥梁恒载期，动态灰色模型改进后的比改进前的模型精度有所提高；灰色动态预测模型和灰色静态模型相比较，动态的在精度、后验差比值都要优于静态灰色模型。

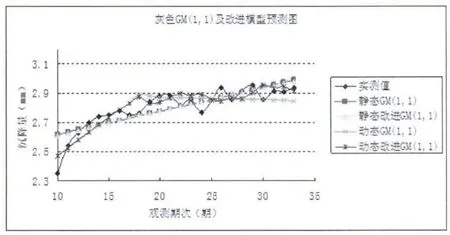
DK1135+667观测点预测图

（3）动态模型用固定维数数据建模，建模的数据预测序列用新预测的数据值充当建模的数据序列，所以动态的预测效果要优于静态模型。

[1]黄声享，尹晖，蒋征.变形监测数据处理[M].武汉:武汉大学出版社，2003.

[2]赵振海.沉降预测与分析的灰色系统预测[J].公路交通科技，应用技术版,2007.

[3]姜鹏，张德军.灰色理论在路基沉降预测中的应用及其改进[J].山西建筑，2007.

[4]李斌，朱健.非等间隔灰色GM(1，l)模型在沉降数据分析中的应用[J].测绘科学，2003.