Ta间隙固溶体中的耦合弛豫*

林国淙，刘 晖，丁喜冬，张进修

(中山大学光电材料与技术国家重点实验室∥物理科学与工程技术学院，广东广州 510275）

弛豫是在外力的作用下系统从一个平衡态过渡到另外一个平衡态时经历的过程，是自然界中普遍存在的现象。内耗和力学谱是研究弛豫过程的重要手段［1－5］。

弛豫过程是一个热激活过程，必须克服高度为ΔH的能垒 (ΔH又被称为激活焓，一般不随温度变化)，弛豫时间τ随温度T的变化满足以下关系

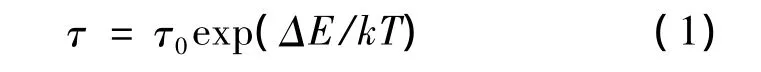
这就是Arrhenius方程，其中k为玻尔兹曼常数，元本身性质的物理量。

(3)式中激活焓ΔH与弛豫元本身的性质有关，弛豫元的耦合影响组态熵ΔS，从而影响表观激活自由能ΔG。当温度T趋近TC时，弛豫时间τ趋于无穷大，弛豫过程被冻结，故TC符合自发有序温度或冻结温度的定义。自发有序温度TC与弛豫元之间的耦合有关，耦合越强，TC越高，TCΔS对表观激活自由能ΔG的影响越大;对于低弛豫元浓度的材料，弛豫元间的耦合可以忽略，虽然熵变ΔS不为零，但TC=0，使TCΔS=0，对表观激活自由能ΔG的影响为0，广义Arrhenius方程 (3)式还原为Arrhenius方程 (1)式。

对ln τ－T实验数据作图，预设不同的T0代替TC，以广义Arrhenius方程进行曲线拟合，拟合参数为ln τ0和ΔG/k，得到不同的标准差SD;在标准差SD最小值附近，把自发有序温度TC也作为拟合参数，得到标准差SD最小值时的自发有序温度TC、指数前因子τ0和表观激活自由能ΔG;如果标准差SD没有最小值，则自发有序温度TC=0，广义Arrhenius方程 (3)式还原为Arrhenius方程(1)式，拟合可以得到指数前因子τ0和表观激活自由能ΔG=激活焓ΔH。

以TC附近的温度T0代替TC代入公式 (3)，得到不同的ΔG，由公式 (3)看出，对T0－ΔG数据作图，线性拟合的截距为激活焓ΔH，斜率的负值为熵的变化ΔS;该方法对TC附近标准差SD急剧变化的高弛豫元浓度材料不适用，因为这时TC附近的标准差SD偏大，得到的ΔG已经不可靠，但由于激活焓ΔH与弛豫元本身的性质有关，可以取低弛豫元浓度的激活焓ΔH来代表高弛豫元浓度的激活焓ΔH，利用拟合得到的表观激活自由能ΔG和自发有序温度TC计算组态熵的贡献TCΔS和熵的变化ΔS。

另外，由指数前因子τ0、熵的变化ΔS和公式(4)可以计算参数τ'0，一个反映弛豫元本身性质的物理量。

综上所述，由实验数据和广义Arrhenius方程可以得到 τ0、TC、ΔG、ΔH、ΔS 和 τ'0。τ0称为指数前因子。这原来是一个经验方程，Zener等人从热力学的基本原理出发，得到了弛豫过程的Arrhenius方程［6－7］，使之成为理论公式。Arrhenius方程一直得到广泛应用。

近几十年来，科学家们发现弛豫时间τ随温度T的变化满足非Arrhenius关系的实验现象越来越多，较大浓度下点缺陷的弛豫就是其中的一种非Arrhenius现象。

人们尝试各种方程来描述非Arrhenius现象，较多使用的是描述高聚物玻璃化弛豫的VFT经验方程 (Vogel-Fulcher-Tamman方程［8］)，它以一个约化温度 (T－T0)代替了Arrhenius方程的温度T，得到其中T0为参考温度，表示弛豫过程被“冻结”的温度。因为根据 (2)式，当温度T趋近T0时，弛豫时间τ趋于无穷大，弛豫过程被冻结。

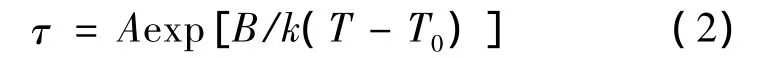
非Arrhenius现象虽然多种多样，但弛豫元之间的互相耦合或关联 (coupling或correlation)都起了重要作用［9－10］，因此，组态熵在弛豫过程中起到重要作用。陈岚［11］从滞弹性理论出发，对弛豫元之间存在耦合的情况进行讨论，得到广义Arrhenius方程其中TC、ΔG、ΔH和ΔS分别为弛豫过程的自发有序温度、表观激活自由能、激活焓和熵的变化量。

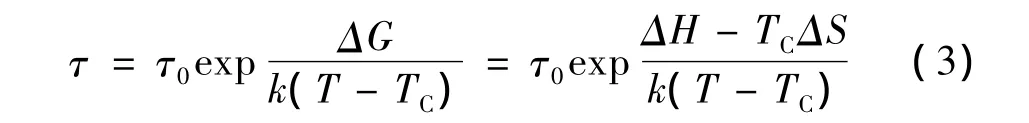
(3)式中指数前因子τ0满足以下关系

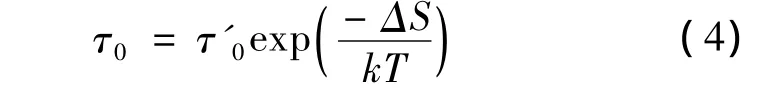
指数前因子τ0包含了熵的贡献，τ'0才是反映弛豫

1 数据处理

数据来自文献 ［12－13］中不同氧的质量分数和不同氮的质量分数的Ta间隙固溶体的内耗实验结果。曲线扫描后由原文图上的坐标获得不同氧的质量分数和不同氮的质量分数的Ta间隙固溶体的的温度T和归一化内耗Q/数据，分别如图1、图2所示。

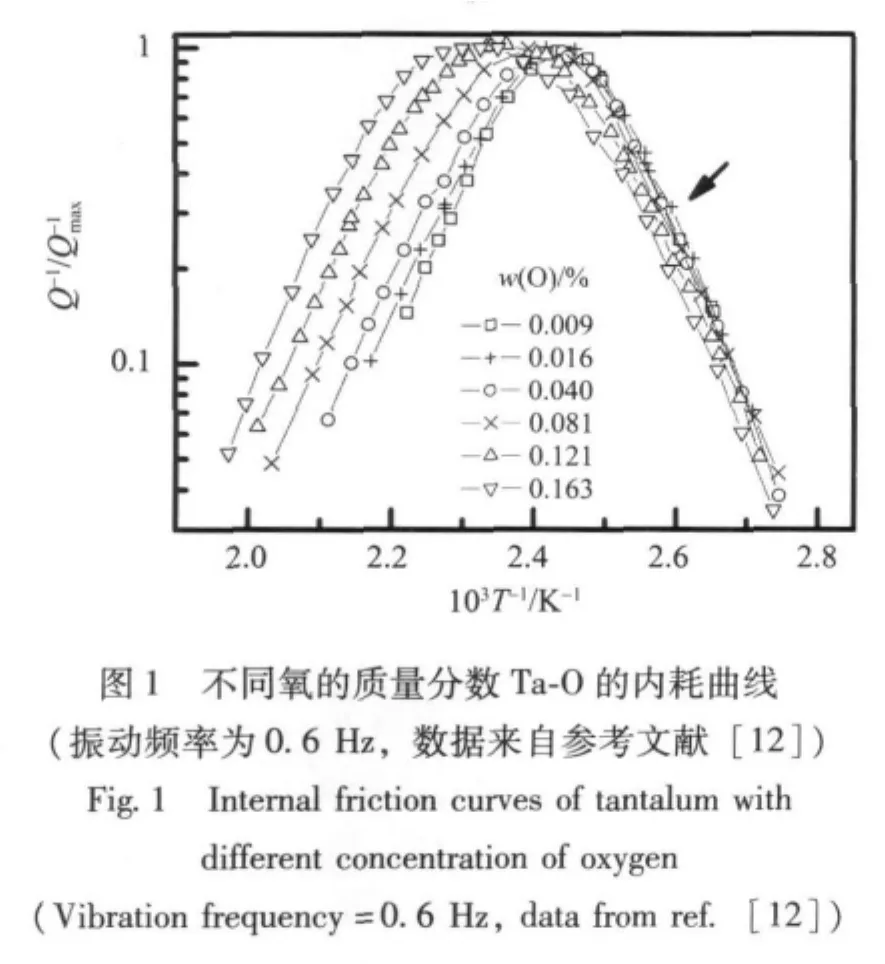
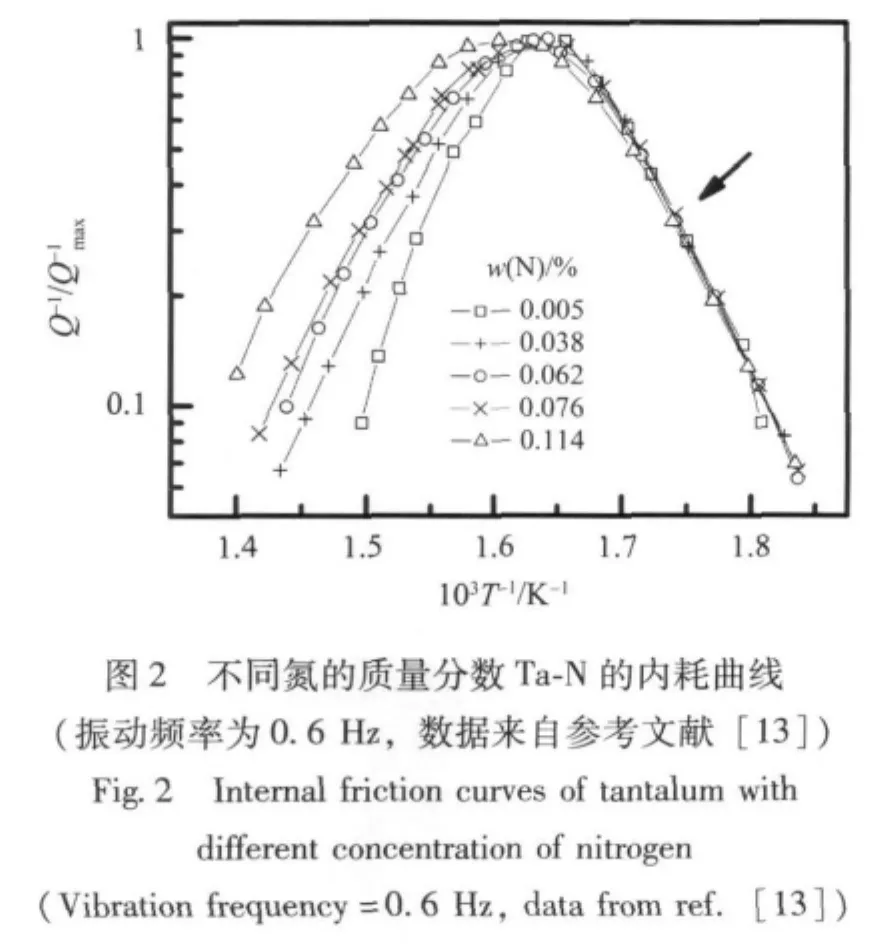
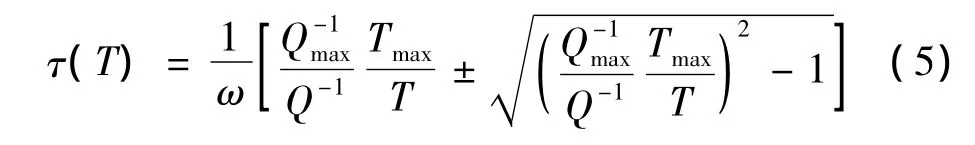
得到ln τ－T数据。公式 (5)中，ω为振动角频率，Tmax为内耗Q－1=时对应的温度，公式中的±号在T＜Tmax时取+号。氧和氮的质量分数(w)和原子个数百分比 (N)及对应的Tmax见表1。

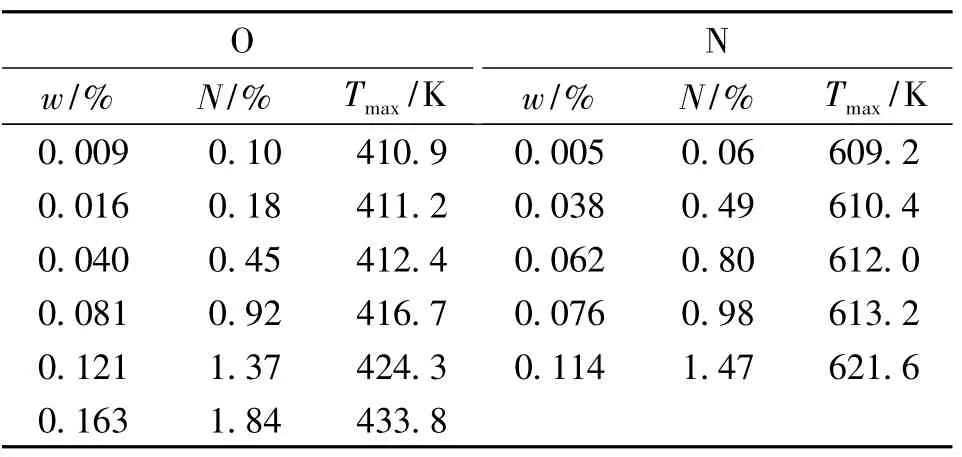
表1 氧含量、氮含量及对应内耗曲线的TmaxTable 1 Concentration of oxygen or nitrogen and Tmax of their internal friction curves

2 结果和讨论

在图1内耗曲线的右端 (图中箭头所示)，T＜Tmax，为相对低温部分，温度对弛豫元耦合的影响较小，选作本文讨论的对象，得到不同氧的原子个数百分比［N(O)］的ln τ－T关系如图3所示，其中的实线为标准差SD最小值时广义Arrhenius方程的拟合曲线。

对图3中不同氧的原子个数百分比［N(O)］的ln τ－T数据，从0 K开始，预设不同的T0代替TC，以公式 (3)进行曲线拟合，拟合参数为ln τ0和ΔG/k，得到不同的标准差平方 SD2，对不同N(O)Ta-O得到的结果如图4所示。

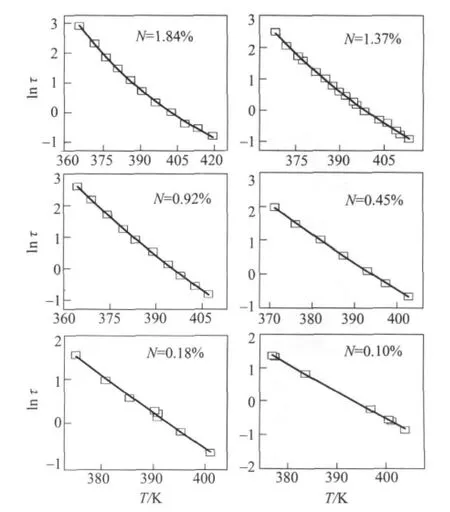
图3 不同N(O)Ta-O的ln τ －T关系Fig.3 Plots of ln τ vs T of tantalum with different concentration of oxygen

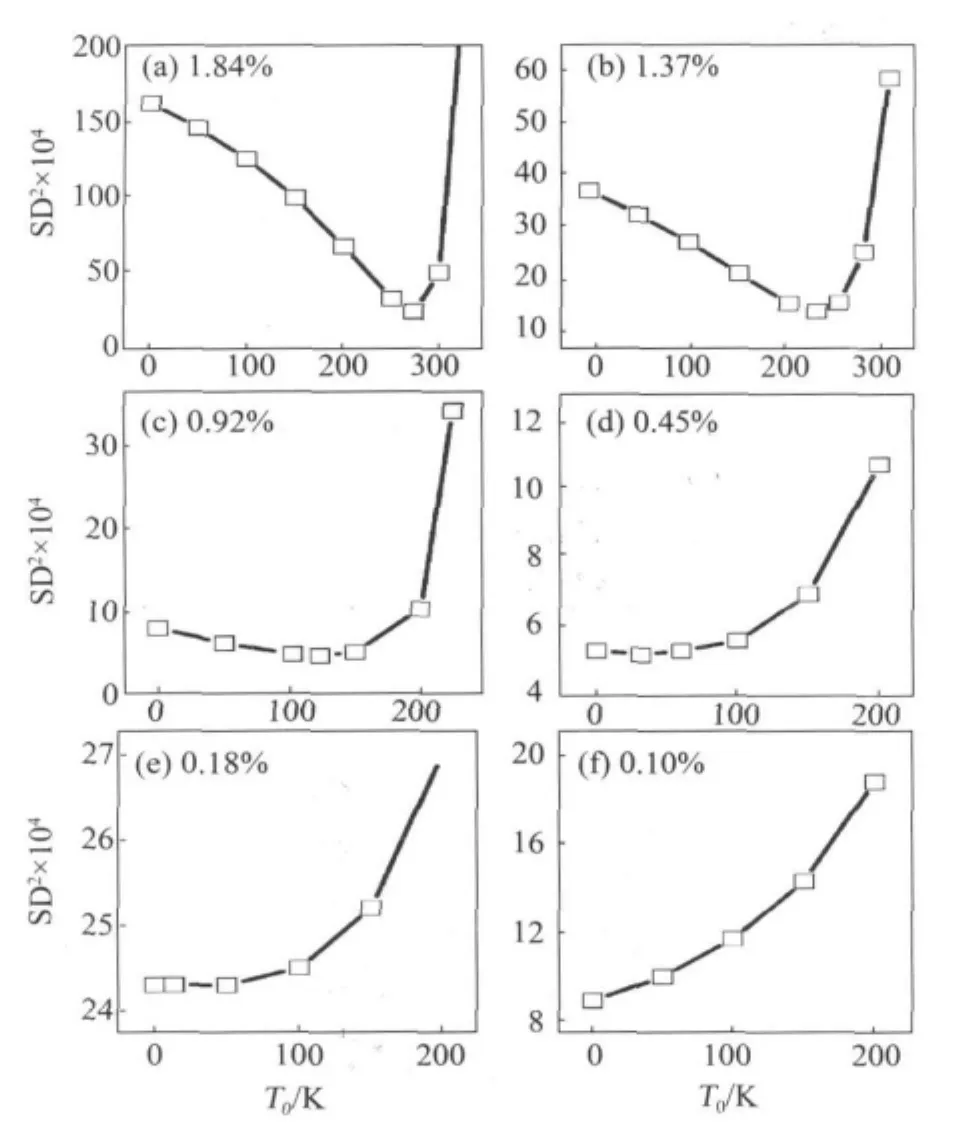
图4 不同N(O)Ta-O的T0-SD2关系Fig.4 Plots of T0vs SD2of tantalum with different concentration of oxygen

在标准差平方SD2最小值附近，把ln τ0、ΔG/k和TC作为拟合参数，得到标准差平方SD2最小值时不同N(O)Ta-O的自发有序温度TC(见图5)、ln τ0(见图6(b))和表观激活自由能 ΔG(见图6(a))。

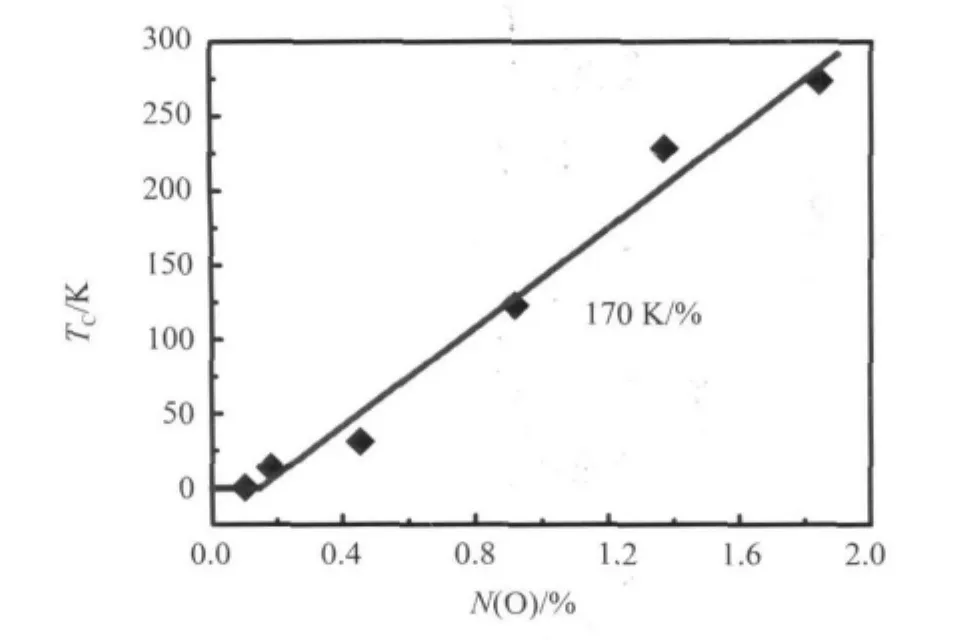
图5 不同N(O)Ta-O的自发有序温度TCFig.5 Self-induced ordering temperature TCof tantalum with different concentration of oxygen

由图5可以看出，N(O)超过一定浓度，自发有序温度TC与N(O)基本上成正比的关系，斜率约为170 K/%。自发有序温度TC与弛豫元之间的耦合有关，耦合越强，TC越高。图5的结果显示，N(O)较低时，TC=0，弛豫元之间没有耦合，随着N(O)的增加，氧原子之间的耦合增加。

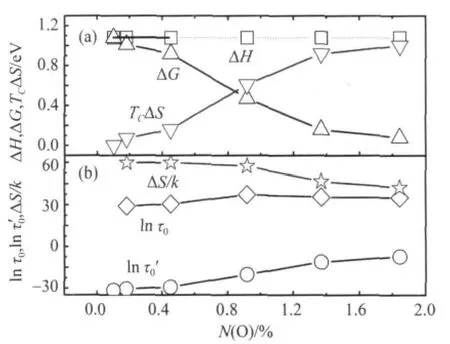
图6 不同N(O)Ta-O的 ΔH、ΔG、TCΔS、ln τ0、ΔS/k 和 ln τ'0 结果Fig.6 ΔH，ΔG，TCΔS，ln τ0，ΔS/k and ln τ'0of tantalum with different concentration of oxygen

由图6可以看出，随着N(O)的增加，ln τ0增加，表观激活自由能ΔG下降。

以TC附近的温度T0代替TC代入公式 (3)，得到不同的ΔG，对T0－ΔG数据作图，线性拟合的截距为激活焓ΔH，斜率的负值为熵的变化ΔS。

对较低N(O)的3个Ta-O固溶体 (N=0.10%、0.18%和0.45%)，表观激活自由能ΔG由1.08 eV下降至1.01和0.92 eV，得到的激活焓ΔH都是1.08 eV，说明激活焓ΔH与弛豫元本身的性质有关，该结果与文献 ［9］中Ta-O固溶体激活焓ΔH=1.09 eV十分接近。

对较高N(O)的3个Ta-O固溶体 (N=0.92%、1.37%和1.84%)，TC附近标准差SD变化急剧 (见图4)，TC附近的标准差SD偏大，得到的ΔG已经不可靠，故以上线性拟合计算激活焓ΔH和熵的变化ΔS的方法不适用。由于激活焓ΔH与弛豫元本身的性质有关，故以较低N(O)的激活焓ΔH=1.08 eV来表示不同N(O)的激活焓ΔH(图6中以虚线表示)，利用已经得到的表观激活自由能ΔG和自发有序温度TC计算组态熵的贡献TCΔS和ΔS/k，如图6所示。

由图6(a)可以看出，随着N(O)的增加，氧原子之间的耦合增加，自发有序温度TC升高，TCΔS对表观激活自由能ΔG的影响增大，使ΔG下降。

利用以上计算得到的 ln τ0和 ΔS/k，由公式(4)可以得到不同N(O)的ln τ'0，如图6(b)所示。从图中可看出，随着N(O)的增加，ln τ0增加，ΔS/k下降，但ln τ'0基本不随N(O)变化，这是因为指数前因子τ0包含了熵的贡献，τ'0才是反映弛豫元本身性质的物理量。

ln τ'0基本不随N(O)变化说明不同N(O)的弛豫元是相同的，也验证了以上使用同一个激活焓ΔH=1.08 eV进行计算是合理的。因为由同一个激活焓ΔH出发，计算熵的变化ΔS和ln τ'0，最后得到的“ln τ'0基本不随氧含量变化”这一结果与“同一个激活焓ΔH”这一条件是自洽的，说明了不同N(O)的弛豫元是相同的，是耦合的单个弛豫元。

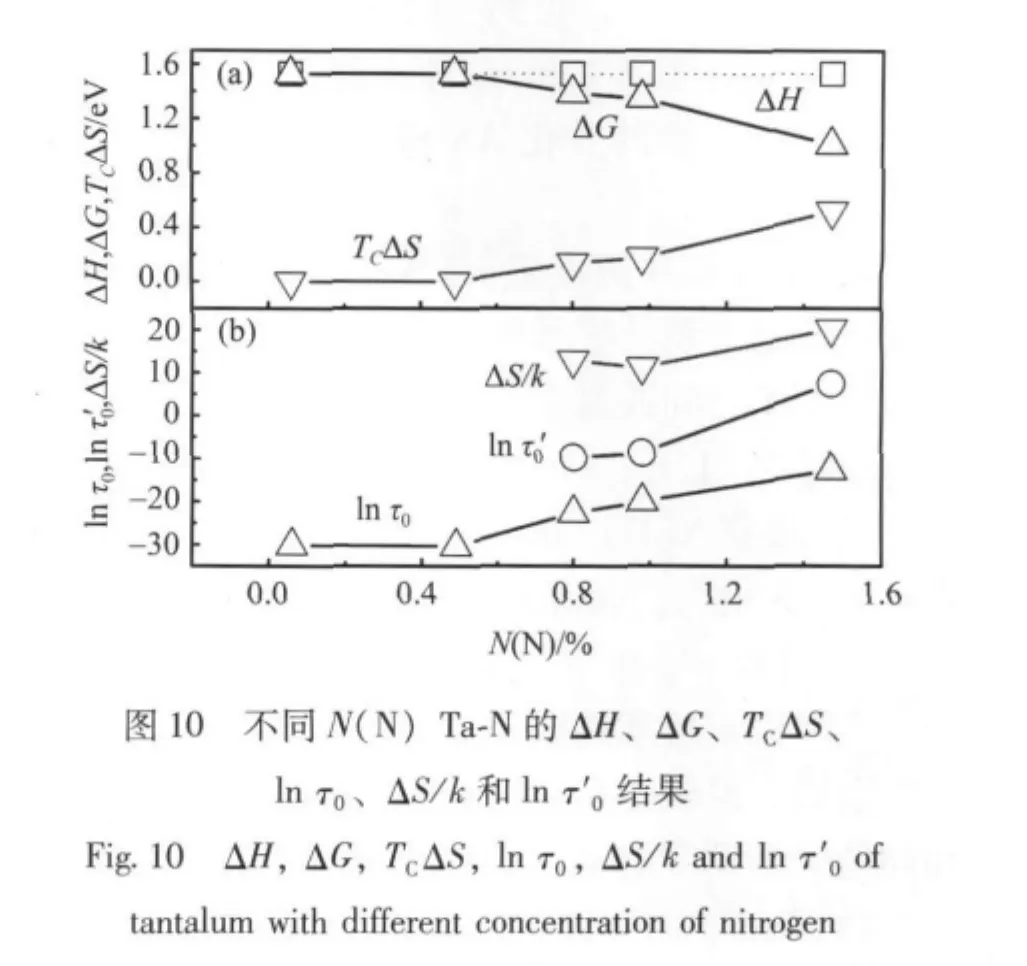
以同样的方法对图2中不同氮的原子个数百分比［N(N)］Ta-N的内耗曲线进行讨论，得到不同N(N)Ta-N的ln τ－T关系 (见图7，其中的实线为标准差SD最小值时广义Arrhenius方程的拟合曲线)，不同N(N)Ta-N的T0-SD2关系 (见图8)，不同N(N)Ta-N的自发有序温度TC(见图9)，和不同 N(N)Ta-N 的 ΔH、ΔG、TCΔS、ln τ0、ΔS/k和 ln τ'0结果 (见图10)。

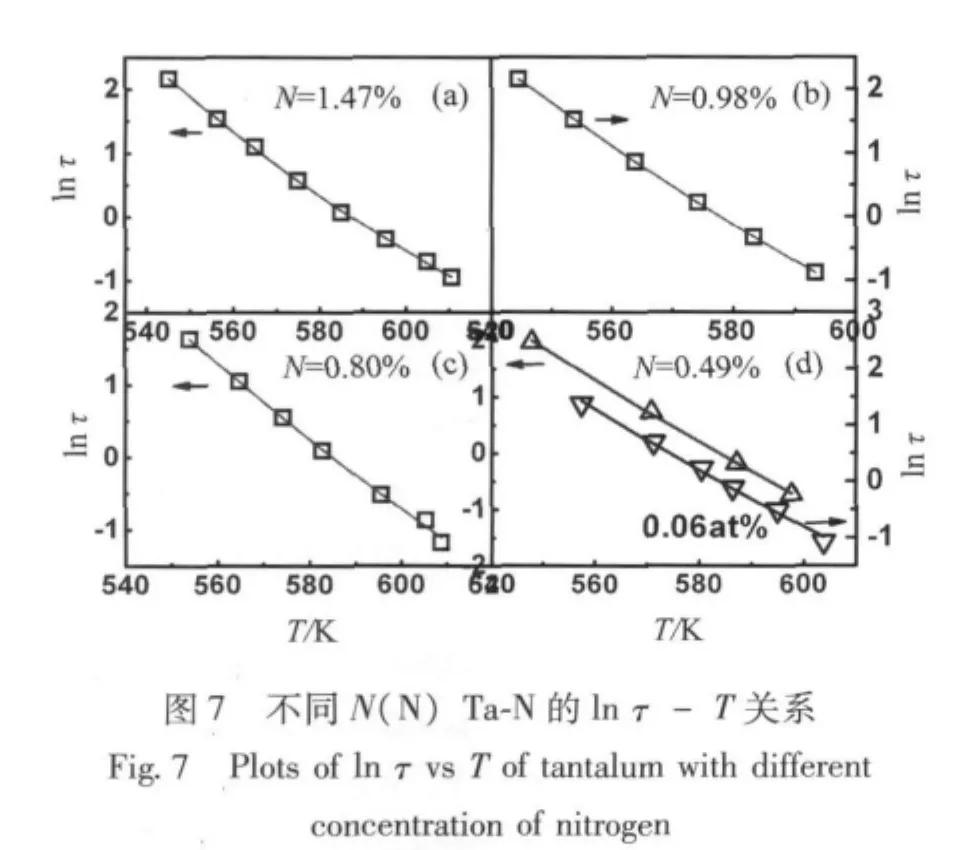
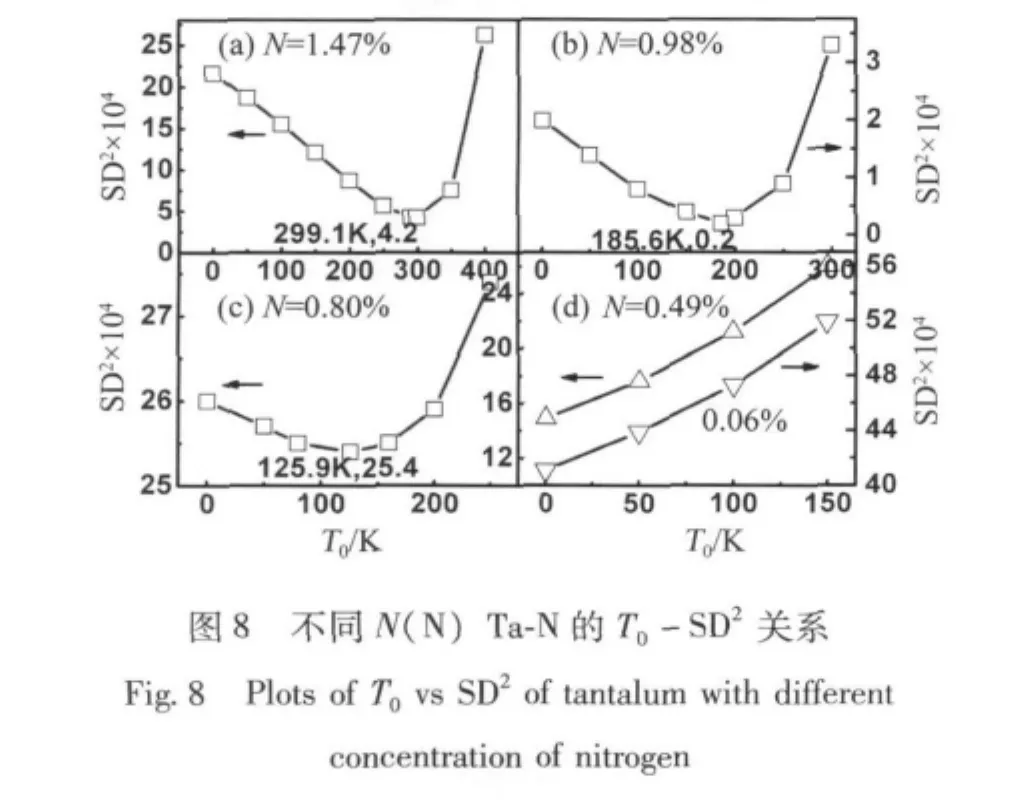
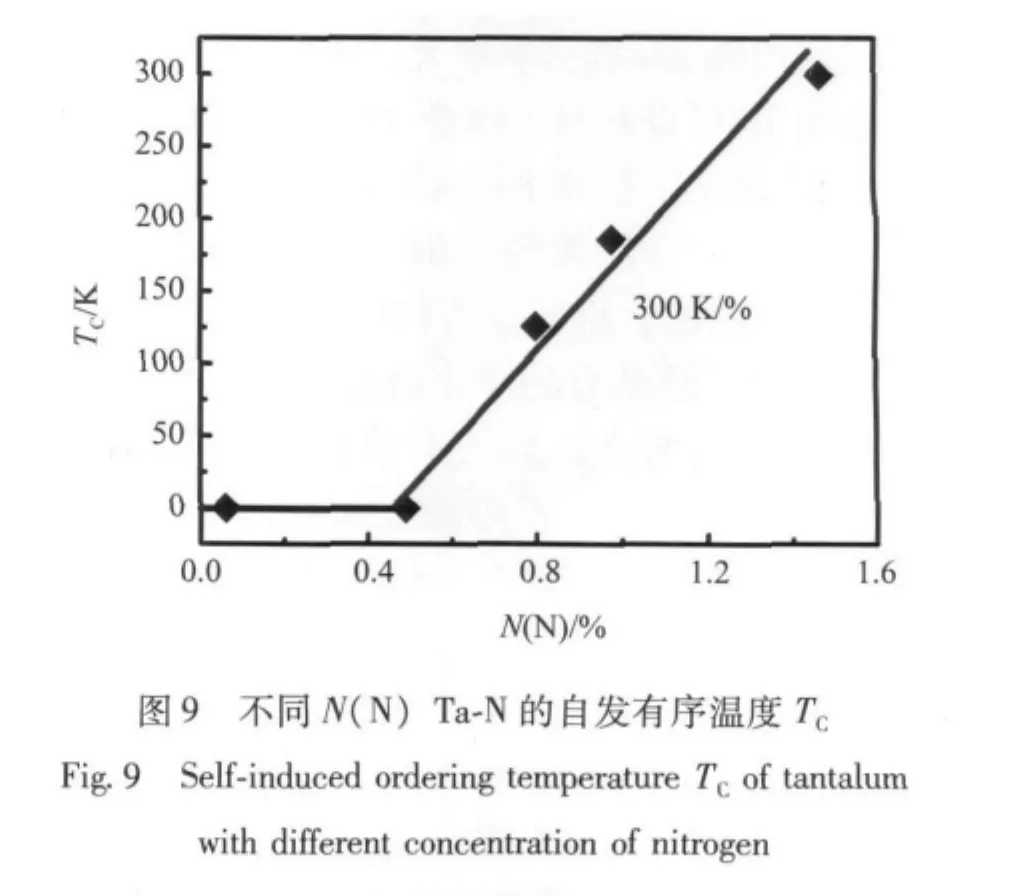
由图9可以看出，N(N)超过一定浓度，自发有序温度TC与N(N)基本上成正比的关系，斜率约为300 K/%。图9的结果显示，N(N)较低低时，TC=0，弛豫元之间没有耦合，然后随着N(N)的增加，氮原子之间的耦合增加。与图5比较，自发有序温度TC随N(N)的升高比随N(O)的升高快，可能与N—N之间的相互作用较大有关。

对较低N(N)的2个Ta-N固溶体 (N=0.06%和0.49%)得到的激活焓ΔH分别是1.52和1.53 eV，该结果与文献 ［9］中Ta-N固溶体激活焓ΔH=1.59 eV十分接近。以较低N(N)的激活焓ΔH=1.53 eV来表示不同N(N)的激活焓ΔH，利用已经得到的表观激活自由能ΔG和自发有序温度TC计算组态熵的贡献TCΔS和ΔS/k(见图10)，结果显示，随着N(N)的增加，氮原子之间的耦合增加，自发有序温度TC升高，TCΔS对表观激活自由能ΔG的影响增大，使ΔG下降。

从图10可以看出，随着N(N)的增加，ln τ0增加，但 ln τ'0在0.8% ～1.0%范围基本不随N(N)变化，这一结果与“同一个激活焓ΔH”这一条件是自洽的，说明了N(N)不太大时的弛豫元是相同的，是耦合的单个弛豫元。N(N)较大时，ln τ'0变化较大，ΔS变化也较大，显示弛豫元发生了变化，可能出现弱耦合的弛豫元对等，使ΔS增大，这时使用较低N(N)的激活焓 ΔH=1.53 eV已不适宜。

3 结论

以广义Arrhenius方程对Ta间隙固溶体的内耗数据进行曲线拟合，得到不同N(O)和不同N(N)的自发有序温度TC、ln τ0和表观激活自由能ΔG、激活焓ΔH、熵的变化ΔS和ln τ'0，得到以下结论:

1)自发有序温度TC与N(O)或N(N)基本上成正比的关系，显示随着N(O)及N(N)的增加，氧原子之间或氮原子之间的耦合增加，使自发有序温度TC上升;

2)随着N(O)或N(N)的增加，组态熵的贡献TCΔS增大，表观激活自由能ΔG下降;

3)参数τ'0基本不随氧含量变化，这一结果与“不同含氧量具有同一个激活焓ΔH”这一条件是自洽的，说明了在讨论的N(O)范围弛豫元是相同的，是耦合的单个弛豫元;

4)N(N)小于1.0%时，弛豫元是耦合的单个弛豫元;N(N)较大时，弛豫元发生变化，可能出现弱耦合的弛豫元对等，使ΔS增大。

［1］NOWICK A S，BERRY B S.Anelastic relaxation in crystalline solids［M］.New York:Academic Press，1972.

［2］葛庭燧.固体内耗理论基础(晶界弛豫与晶界结构)［M］.北京:科学出版社，2000.

［3］朱震刚，郭丽君，尚淑英.能量耗散技术探索液态物质结构的新进展［J］.物理学进展，2006，26(3/4):283－288.

［4］张进修，熊小敏，丁喜冬，等.凝聚态物质的切变波共振吸收谱仪的工作原理［J］.中山大学学报:自然科学版，2001，40(S1):283－288.

［5］林国淙，熊小敏，丁喜冬，等.液体膜切变波共振吸收谱仪的研制与应用［J］.中山大学学报:自然科学版，2005，44(4):129 －131.

［6］LIDIART A B.Encyclopidea of Physics［M］.Berlin:Springer，1957.

［7］DIENES J G，VINEYARD G H.Radiation Effects in Solids［M］.New York:Wiley(inter-science)，1957.

［8］ANGELL C A，NGAI K L，MCKENNA G B，et al.Relaxation in glassforming liquids and amorphous solids［J］.J Appl Phys，2000，88(6):3113－3157.

［9］KIVELSON S A，ZHAO X，KIVELSON D，et al.Frucstration-limited clusters in liquids ［J］.J Chem Phys，1994，101:2391－2397.

［10］TANG X P，GEYER U，BUSCH R，et al.Diffusion mechanisims in metallic suppercooled liquids and glasses［J］.Nature，1999，420:160 －162.

［11］陈岚.广义Arrhenius关系及其在材料研究中的应用［D］.广州:中山大学，2007.

［12］POWER R W.Internal friction in solid solutions of oxygen-tantalum［J］.Acta Metallurgical，1955，3:135 －139.

［13］POWER R W，MARGRET V D.Internal friction in solid solutions of tantalum［J］.Acta Metallurgical，1956，4:233－242.

［14］WELLER M，LI G Y，ZHANG J X，et al.Accurate determination of activation enthalpies associated with the stress-induced migration of oxygen or nitrogen in tantalum and niobium ［J］.Metalluagica，1981，29:1047－1054.