基于威布尔模型的高校大型仪器设备预防维修周期研究

许 蓉，吕凤林

（重庆大学 生物工程学院，生物流变科学与技术教育部重点实验室，重庆 400030）

近年来，为了增强教学和科研实力，培养优秀的科技人才，各高校不断加大在实验室建设方面的投入，购置了大量先进的大型精密仪器设备［1］。仪器设备的复杂性使其发生故障的时间变得很难预测，故障发生的可能性也大大增加。为了提高仪器设备的完好率，使仪器设备的性能总是处于良好状态，维护的重要性日益彰显。然而频繁的维护又会使得维护成本增加，并降低仪器设备有效利用率。这就需要建立一个科学的维护周期，使维护工作发挥最大功效，提高仪器设备的使用效率，降低因故障产生的各种损失。

1 预防维修的重要性

常见的仪器设备维护有3种：更换（事后维护）、预防维修和小修（改善性维护）。更换是用新的同型系统来更换正在工作或者已经失效的系统，在系统失效前更换为预防更换，在系统失效后更换为事后更换，一般认为事后更换费用大于预防更换费用。预防维修则是在系统失效前的某一时刻进行维修，普遍假设修复后可以如新，通常预防维修费用比更换费用小。小修即不改变系统失效的维修［2－3］。

由于预防维修是通过计划性的方法来避免仪器设备故障的发生，是提高设备可靠性、防止设备故障以及减少维护成本的重要手段，一直是仪器设备维护方面的研究热点［4－5］。基本的预防维修方式有2种：一种是依赖于运行时间的定时维修，另一种是依赖于对系统状态监视的维修方式。由于后者花费较大，模型也更为复杂，某些监测技术手段也尚未解决，所以目前得到广泛应用的仍是定时预防维修方式［6］。

虽然有研究表明，进行有效的预防维修可使计划外停产减少50%［7］，然而这方面的研究与应用一般集中在生产企业的生产线管理或大型供应企业的硬件维护，如供电系统变压器的维护等，在高校的大型仪器设备的维护管理方面应用十分少见。

随着高校实验室的不断发展，大型、复杂仪器设备将会越来越多。如果能够避免在仪器设备出了故障后才求助主管部门［8］，争取在仪器设备正常工作的时间段内、在合理的时间点进行预防维修，不仅可以提高仪器设备的使用效率，降低仪器设备的故障率，更能够减少故障维修费用。所以将科学维护的理论应用到高校大型仪器设备管理实践中来，对于高校的大型仪器设备维护管理具有重要的意义。

2 仪器设备预防维修模型的构建

为了建立合理的维修制度，首先应建立科学的维修模型以进行指导。大型仪器设备的故障率随时间的变化的关系如图1所示。仪器设备的故障期可分为磨合故障期（早期故障期）、偶然故障期（偶发故障期）和损耗故障期［9－10］。但是，图1中的仪器设备故障率曲线只能定性地反映故障发生的整体趋势，无法定量地反映出故障分布的具体情况，因此需要引入仪器设备的寿命分布。

常用的寿命分布有指数分布及威布尔分布。由于指数分布通常用于描述小型仪器，而威布尔分布在有限时间区间内对大型仪器设备的符合性较好，故应用相对广泛［11］。本文也采用威布尔分布描述高校大型仪器设备的寿命分布。

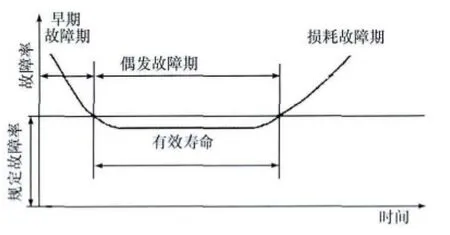
图1 大型仪器设备的典型故障率曲线（浴盆曲线）

2.1 两参数威布尔分布的参数确定

两参数威布尔分布的表达式为

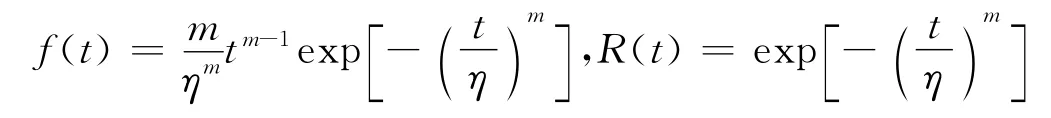
其中f（t）为概率密度函数，R（t）为分布函数，m 为形状参数，η为尺度参数，t为设备寿命。在此分布下的设备故障率表达式为则得其反函数

通常我们需要通过仪器设备的统计寿命推算出符合威布尔分布的2个参数m及η，才能建立符合实际情况的威布尔分布模型。根据威布尔分布的均值公式：

和方差公式［12］：

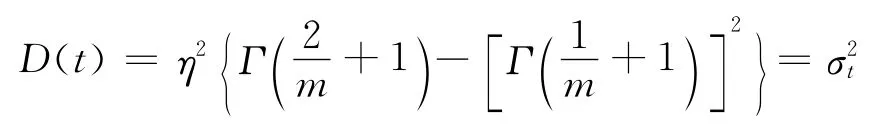
可以近似计算出威布尔分布参数m和η。其中：

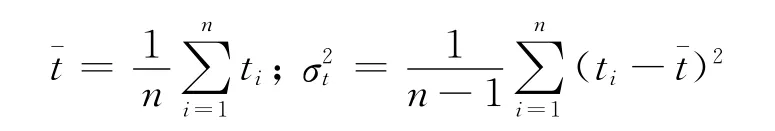
求出威布尔分布的2个参数是确定预防维修周期的重要前提。

2.2 预防维修决策及周期

假设预防维修周期为T，维修作业时间很少，可以忽略不计，优化目标使单位时间内维护费用率最低［13－14］。为预防维修中更换或修复未发生故障的零件费用记为Cm，更换或修复发生故障后的总费用为Cf，在所有情况下都有Cf＞Cm，一个时间段内设备的运行总费用有如下关系：［1－R（T）］，（Cf＞Cm）［15－16］。

由图1所示，在早期故障阶段，λ（t）是随时间递减的函数，即为m＜1的威布尔分布，此时故障率递减，预防维修没有实际意义。在偶发故障阶段，λ（t）为常数，不需要进行任何预防维修，但故障维修可恢复设备的原有状态，但故障率未改变。在损耗故障阶段，λ（t）是随时间递增函数，即为m＞1的威布尔分布。已知Cf＞Cm，在递增故障率情况下，预防维修周期越短越好。根据公式可知，只有当T→∞，R（T）→0时，单位时间的平均费用才最小［17］。

所以，预防维修发生在仪器设备处于故障率递增阶段，即损耗故障期，且Cf＞Cm的情况下才有意义。此时假设Cf≫Cm，维修周期T≪η，则可以得到

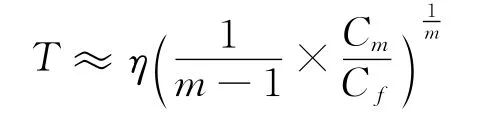
以及与T对应的单位时间费用［18］

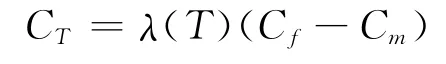
3 应用举例

根据上述的推导，可知威布尔分布的两参数的近似求解方法以及大型仪器设备预防维修的周期确定公式，为了更直观地运用到实际中，下面给出实例，并在Matlab7.4环境下自编程序进行计算，使预防性维护能简便地运用到大型仪器设备的日常管理中。

以激光共聚焦显微镜为例，其主要部件为激光器，根据统计，其有效工作时间（小时）为H＝［3753 5038 5581 3851 7620 5102 6909 3714］，平均每次预防维修的费用Cm为1万元，平均每次故障维修费用Cf为20万元，则威布尔分布的均值E（t）＝¯t及方差D（t）＝σ2t可以计算得出，在Matlab软件中由以下程序实现。

其中形状参数m≈3.97，尺度参数η＝A≈5 735.03。则根据前文公式将求得的参数代入，得到维修周期T≈2 049小时，CT＝6.1945e－4（万元／小时）≈6.2（元／小时）。

4 结束语

预防维修是通过定期的维修来减少、避免故障维修，这对提高仪器设备利用率及减少维修费用都大有裨益。随着高校对实验室建设的不断投入，将预防维修引入高校大型仪器设备的维护是十分必要的。所以对不同的仪器设备确定合理的预防维修周期及进行预防维修的费用估算是科学维护仪器设备的前提。本文运用威布尔分布结合实际算例，给出了确定两参数的方法，并自编程序进行计算，以此推算出合理的预防维修周期及费用，可以为高校大型仪器管理中引入预防维修、改进仪器设备管理提供一定的参考。

（

）

［1］谷淑波，樊广华，于振文.高校大型精密仪器发挥作用的几个关键环节［J］.实验技术与管理，2009，26（3）：170－171.

［2］王文义，张洪芬.维修策略的概念、方法和模型（I）［J］.运筹与管理，1997，6（2）：95－99.

［3］罗佐明.仪器设备的维修与管理［J］.实验技术与管理，1989，6（1）：41－42.

［4］奚立峰，周晓军，李杰.有限区间内设备顺序预防性维护策略研究［J］.计算机集成制造系统，2005，11（10）：1465－1468.

［5］周晓军，奚立峰，李杰.一种基于可靠性的设备顺序预防性维护模型［J］.上海交通大学学报，2005，39（12）：2044－2047.

［6］胡睿，孙磊，王平.定时预防维修方针和策略的数字仿真分析［J］.舰船电子工程，2006，26（5）：132－134.

［7］Oday Kumar.维修技术和管理［J］.中国设备管理，1997（7）：35－36.

［8］雷川华，范家才，阮学锋，等.创建高校大型仪器设备专业维修模式的探讨［J］.实验技术与管理，2007，24（4）：153－156.

［9］蔡军.化工设备故障分析及预防维修措施［J］.广州化工，2010，38（10）：186－188.

［10］邱仕义.电力设备可靠性维修［M］.北京：中国电力出版社，1998：98－100.

［11］文杰.大型整流装置远程维护系统研究与实现［D］.长沙：中南大学，2008.

［12］张钊，陈金木，陈昊.一种基于可用率约束的电气设备计划维护优化模型［J］.电力系统保护与控制，2011，39（23）：85－88.

［13］三根久，河合一.可靠性、维修性的数理基础［M］.北京：机械工业出版社，1984.

［14］蒋仁言，左明建.可靠性模型与应用［M］.北京：机械工业出版社，1999.

［15］赵艳萍.机械设备预防维修周期的确定［J］.机械科学与技术，1996，25（6）：82－84.

［16］郑殿旺，鲁立刚，荆宏伟，等.汽车最优维护周期的模型解研究［J］.佳木斯大学学报：自然科学版，1999，17（1）：41－43.

［17］程瑾，杨路刚.设备预防维修管理系统研究［J］.微计算机信息，2007，23（30）：40－41，180.

［18］杜清玲，李美芳，刘家科.机械设备预防维修周期的确定［J］.机床与液压，2000（6）：92－94.