基于双绕组等值电路模型的波过程研究

牟晓霞 李冬雪 肖模军

摘要：目前企业在计算波过程时将低压绕组作为接地体，计算结果过于严格，加大了成本开支。文章考虑低压绕组感应过电压的影响，建立了更接近实际情况的双绕组等值电路模型，通过实例计算和实验数据的对比，论证了模型的正确性与通用性，提高了电场的计算精度。

关键词：电力变压器；纵绝缘；电场；波过程；安全裕度

中图分类号：TM422 文献标识码：A 文章编号：1009-2374（2013）29-0007-02

变压器绝缘是衡量变压器性能的一个重要指标，波过程计算作为设计阶段的重要环节，其精度一直是变压器企业关注的热点。由于绝缘结构过于复杂，因此，给电场计算带来很大的难度。以往的波过程模型计算的结果不能真实反映电场情况，基于此本文建立了一种新的波过程计算模型，并且以一台实际变压器为例进行了计算和对比，从而说明模型的正确性，新模型更接近实际情况，计算精度较高。

1 双绕组模型

现如今企业为了简化计算，计算波过程时仍然沿用传统的单绕组等值电路模型，该模型没有考虑低压绕组感应过电压的作用，以牺牲成本为代价，而且对电场的计算精度不够高，因此，本文提出了双绕组等值电路模型。双绕组等值电路模型如图1所示。其中，Lhn表示高压绕组的自感，Mhnj表示高压绕组的互感，Chkn表示高压绕组饼间电容，Chln表示高低压绕组间的电容，Lln表示低压绕组的自感，Mlnj表示低压绕组的互感，Clkn表示低压绕组饼间电容，Cltn表示低压绕组和铁心间的电容。

对图1所示的双绕组等值电路应用网孔电流法解方程，以高压绕组第一饼为例，网孔电流为ih1，根据磁通与电流关系式有，对整个绕组列网孔电流方程有：

其中K1至K3是由电感和电容组成的数学关系式，

V1（t）表示冲击电压。

2 计算实例

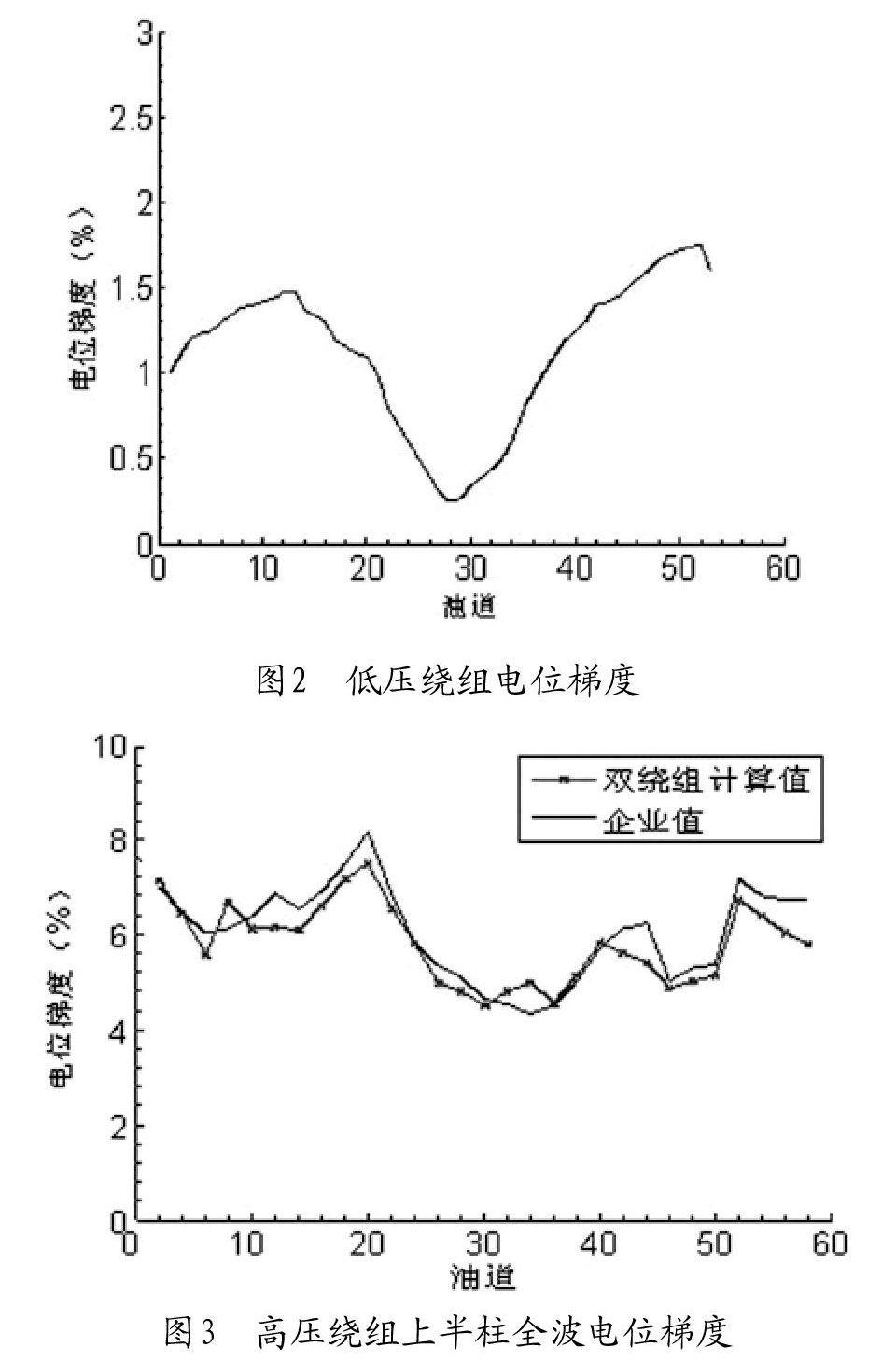
为了验证双绕组模型的正确性，本文对一台500kV电力变压器进行了波过程计算，计算结果如图2和图3所示。

从图2可以看出，低压绕组的电位梯度波动较大，最大值出现在绕组末端，但由于低压绕组是螺旋式绕组，且梯度幅值较小，所以低压绕组的安全度较大。图3说明全波作用时电位最大梯度出现在第20号油道附近，全波作用时双绕组模型计算的电位梯度值是8.05%，实验数据是8.18%；与实验数据的比较验证了双绕组模型的正确性。

上面是对一台普通的电力变压器进行的计算，其结果并不能说明模型的通用性，接下来为了说明双绕组模型的通用性，本文继续以一台结构较为复杂的换流变压器进行了计算，计算结注：上图中虚线代表实验数据，实线代表本文的计算数据。

3 结语

纵绝缘考核的重点是波过程计算，为了提高计算精度，本文提出了一种新的等值电路模型即双绕组等值电路模型。并且以实际变压器为例进行了双绕组模型下的波过程计算，通过与实验数据的比较验证了双绕组模型的正确性和通用性。

参考文献

[1] 郭颖娜，程为彬，王世山.变压器纵绝缘设计中冲

击响应电压分布的仿真分析[J].西安科技大学学报，

2007，27（3）：452-456.

[2] 谢毓诚.电力变压器设计手册[M].北京：机械工业

出版社，2009.

[3] 路长柏.电力变压器纵绝缘技术[M].哈尔滨：哈尔

滨工业大学出版社，1990.

[4] 李道明，曲渝.变压器冲击电压分布计算在纵绝缘设

计中的应用[J].郑州大学学报，2003，24（4）：

28-31.

[5] 朱英.快速暂态过电压及其在变压器绕组上分布的分

析与计算[D].沈阳工业大学，2007.

[6] 路长柏.电力变压器纵绝缘[J].黑龙江电力，2003，

25（1）：8-10.

[7] 顺特电气有限公司.树脂浇注干式变压器和电抗器

[M].北京：中国电力出版社，2005.

[8] 陈慧丹，刘晓玉，陈昊.纳米硅/铝氧化物杂化聚酰

亚胺薄膜电性能研究[J].绝缘材料，2008，41

（6）：37-40.

[9] 林福昌.高电压工程[M].北京：中国电力出版社，

2006.

[10] 刘建军.500kV电力变压器绕组波过程计算与分析

[J].沈阳工程学院学报，2008，4（4）：330-333.

[11] 李众祥.变压器线圈冲击分布测量的研究[D].华北

电力大学，2001.

[12] 陈尔奎，李强，刘文里，等.简易冲击电压分布计

算软件的设计[J].变压器，2004，41（9）：26-30.

[13] 孙海峰.VFTO作用下变压器绕组中波过程及谐振研

究[D].华北电力大学，2004.

[14] 张喜乐，梁贵书，孙海峰，等.VFTO作用下变压器

绕组的过电压计算[J].高电压技术，2005，31

（8）：4-6.

[15] 梁贵书，张喜乐，王晓辉，等.特快速暂态过电压

下变压器绕组高频电路模型的研究[J].中国电机工

程学报，2006，26（4）：144-148.

作者简介：牟晓霞（1963—），女，辽宁铁岭人，铁岭市电力勘测设计院工程师，研究方向：变电所土建设计。