永磁同步电机直接转矩控制调速系统

涂小卫，杨 影，陈 鑫，俞志轩

(上海大学机电工程与自动化学院，上海 200072)

0 引言

交流调速系统具有调速精度高、调速范围广、响应速度快、过载能力强、节能显著等优点，已广泛应用于电力、运输、制造等国民经济领域。永磁同步电动机(PermanentMagnetSynchronous Motor，PMSM)具有结构简单、运行可靠、易维护、体积小、质量轻、效率高等优点，在各个领域得到了广泛应用，因此研究高性能的交流调速系统具有十分重要的现实意义[1]。结合电机控制专用浮点型数字信号处理(DSP)芯片TMS302F28335，设计了PMSM的直接转矩控制系统，采用截止频率随转速同步修改的低通滤波器(Low Pass Filter，LPF)估算定子磁链。在系统中采用了一种简单有效的零矢量电流限幅措施解决起动过流，该系统具有控制结构简单，动态性能好，改善了低速性能等优点。

1 PMSM直接转矩控制原理

1.1 PMSM数学模型

图1 PMSM在不同坐标下的矢量图

PMSM不同坐标系下的矢量图如图1所示，转子同步旋转的dq坐标系，d轴正方向为转子磁链方向;定子同步旋转的xy坐标系，x轴正方向为定子磁链方向;两相静止坐标系αβ，α轴正方向与电机A轴重合。运用坐标变换原理，整理三相PMSM在dq坐标系下的数学模型如下[2]。

式中:ψd，ψq——定子磁链 d，q轴分量;

Ld，Lq——定子 d，q 轴等效电感;

id，iq——定子电流;

ud，uq——定子电压 d，q 轴分量;

ψf——转子磁链;

p——微分算子;

Rs——定子绕组电阻;

ωr——转子机械角速度;

Te——电磁转矩;

np——电机极对数。

PMSM直接转矩控制采用的是定子磁链定向控制，根据定子磁链坐标系下数学模型，经过等效坐标变化可得其直接转矩控制的基本方程为[3]

对于隐极式PMSM，Lq=Ld，故式(4)可写为

1.2 PMSM传统直接转矩控制原理

PMSM直接转矩控制系统结构图如图2所示，主要包括:滞环比较器、开关表、转矩和定子磁链估算三个环节。定子磁链参考值设定为转子磁链幅值，将磁链和转矩的估算值分别与对应参考值滞环比较，得到定子磁链与转矩的控制信号Δψs、ΔTe，并参考定子磁链扇区，查询表1所示的开关表，确定逆变器的开关状态，得到功率器件的控制信号驱动逆变器。表1中电压矢量U0、U1、U2、U3、U4、U5、U6、U7分别对应逆变器三相 Sa、Sb、Sc的开关状态“000”、“001”、“010”、“011”、“100”、“101”、“110”、“111”[4]。

表1 传统直接转矩控开关表

图2 传统直接转矩控制系统结构图

2 定子磁链估算

电压模型是交流调速系统中观测定子磁链的基本方法，其具有算法简单、对电机参数依赖小等优点，所以电压模型磁链观测法一直受到人们的重视。

基于电压模型的定子磁链估算方案采用了纯积分器，但利用理想积分器估算磁链时，定子电流与变频器直流电压的测量误差以及定子电阻参数不准都可能在磁链估算结果中引起畸变。为克服直流漂移问题而采用LPF替代纯积分器估算定子磁链的方案。

LPF的传递函数为τ/(1+τs)，τ为时间常数，其倒数1/τ=ωc为截止频率，可进一步演变为

由式(7)可将LPF看成由高通滤波器(HPF)和纯积分两个环节组成。纯积分正是计算定子磁链所需要的算法，HPF则可以抑制或滤去直流偏移量。

LPF和纯积分的波特图如图3所示，适当的选取截止频率的LPF可以取代纯积分环节，同时可以抑制或滤去直流偏移量。LPF带来的相位和幅值误差，也会带来电压矢量误选的问题，可以采用改变截止频率来减小LPF所带来的幅值和相位的偏差，从而提高性能。根据实际电机转速实时调整截止频率 ωc=kωe，比例系数 k范围为0.1 ～0.5[5]，对低速下的磁链估算误差起到抑制作用，同时在高速时恢复到较高的截止频率，这样就不会影响高速下的稳定性能。

图3 LPF和纯积分的波特图

3 直接转矩控制起动限流措施

由于直接转矩控制系统无电流环，虽然转矩限幅可以限制电流，但在起动的初始过程中电磁转矩为零，转矩限幅无法限制电流，直接利用开关表选择电压矢量自然的起动，将会带来很大的电流冲击而引起频繁的保护动作，甚至会损坏主电路，因此必须采取起动限流措施。

在本系统中采用了一种简单有效的零矢量电流限制措施:加入软件电流限制措施。当电流的检测值达到软件保护阈值时，选择零矢量进行限流;当电流降至保护阈值以下时，则正常按照开关表选择电压矢量[6]。

4 仿真及试验研究

为了验证所提出方案的正确性和可行性，针对同一PMSM分别进行了基于MATLAB/Simulink的仿真验证和实际系统的试验验证。

仿真和试验用PMSM电机参数额定转矩2.39 N·m，极对数 4，定子电阻1.6 Ω，永磁体磁链 Ψf=0.065 8 Wb。交、直轴电感 0.004 H，转动惯量0.000 103 kg·m2额定转速3 000 r/min。磁链滞环宽度设为0，转矩滞环范围设为[－0.01，0.01]。速度环采样周期为2 ms，控制周期为50 μs，直流母线电压50 V，软件电流限幅值为6 A，均在空载下试验，仿真结果如图4、图5所示。

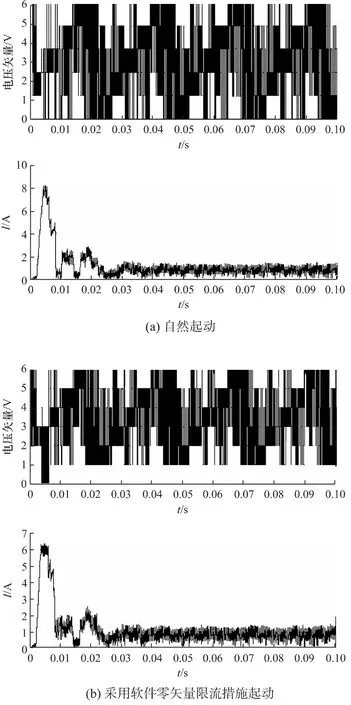
图4 起动时电压矢量和母线电流波形

图5 系统在空载下运行的响应曲线

由图4(a)自然起动波形可看出，起动电流为8 A，超出实际系统中的硬件电路保护值6.67 A，在实际系统中起动失败。图4(b)采用软件零矢量限流措施起动的波形，在检测母线电流超出阈值6 A时选择了零矢量，电流降至保护阈值以下时，则正常按照开关表选择电压矢量，故可以将起动时的电流限制在6 A附近，在实际系统中可顺利起动。对比图4(a)、图4(b)可看出达到稳态的时间均约30 ms，即采用软件零矢量限流措施起动方案对系统快速响应性几乎无影响。图5为系统在20%额定转速、空载下运行稳态时的波形，图5(a)表明系统稳态性能好，图5(b)可看出纯积分会带来累计误差，而采用截止频率随转速同步改变的LPF方案可以很好地跟随真实磁链，估算定子磁链较为准确，图5(c)为给定转速1 000 r/min起动在0.3 s转速跳变到100 r/min，系统经过40 ms达到稳态，系统响应快速，低速性能良好。

为进一步试验验证所提出方案的可行性，搭建了基于浮点型DSP芯片TMS302F28335的直接转矩控制硬件平台，采用电机自带的2 500线增量式光电编码器测速，系统中硬件电路母线电流保护值6.67 A，试验波形如图6～图9所示。

图6 稳态时定子磁链圆

图7 1 000 r/min时磁链(上)和定子磁链扇区(下)

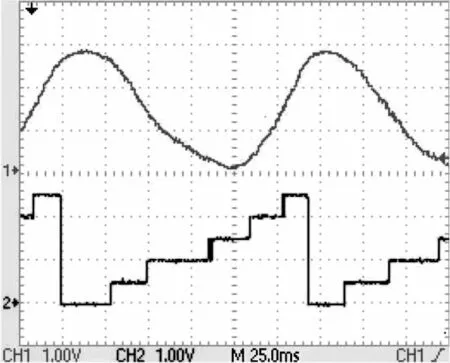
图8 100 r/min时ψα磁链(上)和定子磁链扇区(下)

图9 100 r/min时输出转矩(上)和实际转速(下)波形

图6 为稳态时实际系统的定子磁链圆波形，可见系统稳态性能好。图7和图8为系统空载下，分别在转速1 000 r/min和100 r/min时所对应的定子磁链在α轴的分量和定子磁链扇区波形。对比图7和图8可看出，在高速范围内系统性能良好，而在低速100 r/min时定子磁链和扇区波形有所畸变，但系统总体运行正常。图9为低速100 r/min时输出转矩和实际转速波形，转矩脉动约0.3 N·m，转速波动较大为±30 r/min，系统运行平缓，拓宽了PMSM的调速范围。

5 结语

针对纯积分带来的累计误差问题，采用低通滤波器估算定子磁链的方案，在低速时由转速同步实时修改截止频率，而在高速时恢复较高的截止频率，仿真和试验结果表明，可以改善直接转矩在低速的性能，拓宽了PMSM直接转矩调速范围。系统同时采用了软件零矢量限流措施起动方案，采用零矢量来限制起动电流，仿真和试验结果说明该方案可有效抑制起动电流过大问题，而且保持了传统DTC控制的动态响应快速，控制结构简单的优点，改善了传统DTC的控制性能，但仍存在低速范围噪声大，极低速时运行不稳定的缺点。

[1]韩如成，潘峰，智泽英.直接转矩控制理论及应用[M].北京:电子工业出版社，2012.

[2]田淳，胡育文.永磁同步电机直接转矩控制系统理论及控制方案的研究[J].电工技术学报，2002(2):8-11.

[3]袁登科，陶生桂.交流永磁电机变频调速系统[M].北京:机械工业出版社，2011.

[4]周扬忠，胡育文.交流电动机直接转矩控制[M].北京:机械工业出版社，2011.

[5]HINKKANEN M，LUOMI J.Modified integrator for voltage model flux estimation of induction motor[J].IEEE Trans Ind Electron，2003，50(4):818-820.

[6]胡育文，黄文新，张兰红，等.异步电机(电动、发电)直接转矩控制系统[M].北京:机械工业出版社，2012.