用Excel实现单个正态总体均值的假设检验

刘忠广

(河南工程学院 工商管理学院，河南 郑州 451191)

单个正态总体均值的假设检验可以用SPSS等专业统计软件来实现，但这些专业统计软件的普及性不够.Excel软件具有极强的普及性并且易于操作，其所带的数据分析工具能满足大多数数据处理的要求，但在进行假设检验时，Excel的数据分析工具只提供了两个总体参数检验的方法，而没有专门的对单个总体均值进行检验的现成工具，所以很有必要探讨用Excel进行单个正态总体均值检验的便捷方法.

1 单个正态总体均值检验的传统方法

对于总体均值的检验按照以下步骤来进行：(1)提出假设；(2)构造检验统计量并计算统计量的值；(3)根据给定的显著水平确定临界值和拒绝域；(4)将统计量的值与临界值进行比较，做出决策.下面以实例来说明.

例某医生调查了20个难产婴儿的出生体重，数据如下(单位为kg)：3.88，3.31，3.34，3.82，3.30，3.16，3.84，3.10，3.90，3.18，3.05，3.22，3.28，3.34，3.62，3.28，3.30，3.22，3.54，3.30.已知一般婴儿的平均出生体重为3.25 kg，能否认为难产婴儿的出生体重显著大于一般婴儿(给定显著水平α=0.05).

解(1)提出假设：H0∶μ=3.25,H1∶μ>3.25.

(2)构造检验统计量并计算统计量的值.

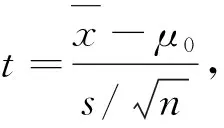
(3)根据α=0.05，查自由度为19的t分布表得临界值为1.729.

(4)将统计量的值与临界值进行比较，统计量t=2.476>1.729，故拒绝原假设，认为难产婴儿的出生体重显著大于一般婴儿.检验结果见图1.

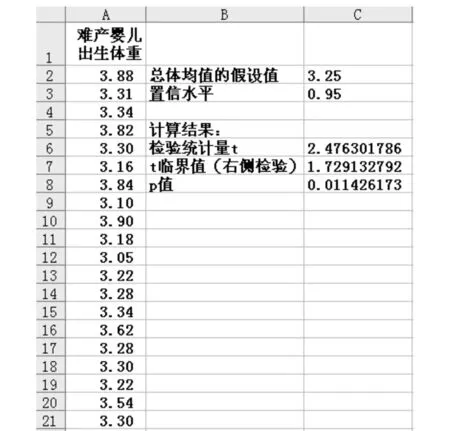
图1 检验结果Fig.1 Result of the test

2 利用Excel的函数工具进行检验

(1)构造工作表[1]. 在单元格A1输入“难产婴儿出生体重”，在A2～A21输入上例中的数据，在B2和C2分别输入“总体均值的假设值”和“3.25”；在B3和C3分别输入“置信水平”和“0.95”；在B6,B7和B8分别输入“检验统计量t”,“t临界值(右侧检验)”和“p值”，如图1所示. C6,C7和C8的数值由下面的函数工具计算.(2)计算检验统计量.在C6单元格输入公式：“=(average(A2∶A21)-C2)/stdev(A2∶A21)/sqrt(count(A2∶A21))”.(3)计算临界值tα，在C7单元格输入公式“=tinv((1-C4),count(A2∶A21)-1)”.(4)计算p值，在C8单元格输入公式“=tdist(C6,count(A2∶A21)-1,1)”.(5)根据以上的计算结果，p值(0.011 426)< 0.05(或统计量t=2.476>1.729 1)，故拒绝原假设，认为难产婴儿的出生体重显著大于一般婴儿.

3 证明两个总体均值之差检验的特殊情形和单个正态总体均值检验的一致性

3.1 两个总体均值之差检验的检验统计量和自由度的确定

在对两个总体均值之差检验时，原假设和备择假设分别有如下几种情况：(1)H0∶μ1-μ2=0，H1∶μ1-μ2≠0；(2)H0∶μ1-μ2≥0，H1∶μ1-μ2<0；(3)H0∶μ1-μ2≤0，H1∶μ1-μ2>0.

使用的检验统计量为

(1)

自由度为

(2)

3.2 两个总体均值之差检验特殊情形下的检验统计量和自由度的确定

现在考虑一种特殊的情形，假设总体2的各个值均为μ0，那么从总体2中抽取的若干个体组成的样本2的各个值也均为μ0，则样本2的均值和方差分别为

(3)

(4)

将式(3)和式(4)代入式(1)和式(2)，则检验统计量为

(5)

自由度为

(6)

3.3 单个总体均值检验时的检验统计量和自由度的确定

在仅对总体1的均值进行检验时，原假设和备择假设分别为

(1)H0∶μ1=μ0，H1∶μ1≠μ0；(2)H0∶μ1≥μ0，H1∶μ1<μ0；(3)H0∶μ1≤μ0，H1∶μ1>μ0.

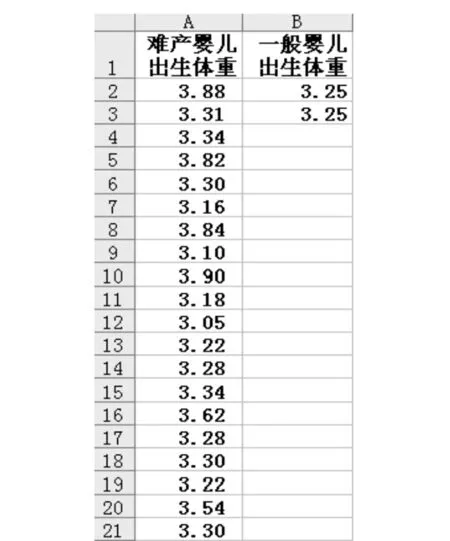
图2 Excel数据Fig.2 Excel data

故上述内容证明了单个正态总体均值的检验和对两个总体均值之差检验的特殊情形(其中一个总体的各个体的值均相等)是一致的,所以对单个总体均值的检验可以利用Excel中的数据分析来实现.

4 实例操作

打开Excel，在单元格A1输入“难产婴儿出生体重”，将上例中的20个数据输入到工作表的A2～A21；在单元格B1输入“一般婴儿出生体重”，B2单元格输入3.25，再将3.25复制粘贴几次即可(最少要有2个数据，因为只有一个数据时无法计算方差,本例为2个数据)，如图2所示，然后按如下步骤操作：

(1)选择【工具】下拉菜单；(2)选择【数据分析】选项；(3)在分析工具中选择【t检验，双样本异方差检验】；(4)当出现对话模型时,在【变量1的区域】方框内输入数据区域A1∶A15,在【变量2的区域】方框内输入数据区域B1∶B3,在【假设的平均差】方框内输入0,在【标志】前的方框内打上“√”,在【ɑ】方框内输入0.05,在【输出选项】中选择输出区域(本例中选择“新工作表”)，如图3所示.然后选择【确定】，输出结果如图4所示.

根据图4中的结果可知，p值单尾(0.011 426)<0.05(或检验统计量t=2.476>单尾临界值1.729 1)，故拒绝原假设，认为难产婴儿的出生体重显著大于一般婴儿.

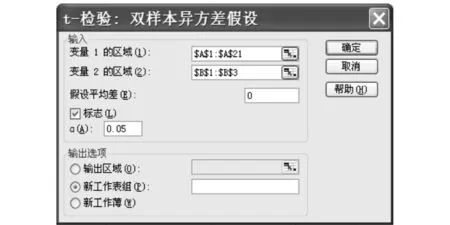
图3 Excel工作表Fig.3 Excel work chart

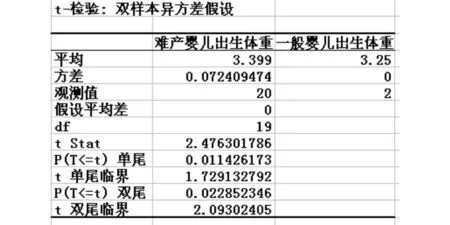
图4 Excel输出Fig.4 Excel output

参考文献：

[1] 袁加军,朱建平.统计基础实验[M].厦门：厦门大学出版社，2010:103.

[2] 贾俊平,何晓群,金勇进.统计学[M].5版.北京：中国人民大学出版社，2012:171.

[3] 庄楚强,何春雄.应用数理统计基础[M].3版.广州：华南理工大学出版社，2006:107.