泾阳台数字地磁信号的干扰分析及去噪处理

鲁 权， 邢西淳， 李西京， 毛 娟

(1.户县地震办公室，陕西 户县 710300；2.陕西省地震局泾阳地震台，陕西 咸阳 713704；3.陕西省地震局乾陵地震台，陕西 咸阳 713300）

0 引言

随着经济的发展，地震台附近开山、爆破、破石等经济活动以及大型电器设备突然启动、关闭或负荷突然改变和重型机动车辆来往频繁等[1、2]，致使泾阳台GM4、FHD-1数字地磁信号的噪声干扰日益严重。这些电磁噪声有的离观测点很近，在某些情况下噪声干扰甚至能大过真实的地磁信号本身，观测到的地磁信号形成尖脉冲、毛刺、台阶干扰。另外地磁观测仪器产生的仪器噪声也会对地磁数据产生干扰[3、4]。泾阳GM4磁通门磁力仪和FHD-1核旋质子磁力仪观测数据，很明显的可以看到两类干扰，一类是仪器供电设备对仪器观测数据的干扰，另一类是上述各种环境干扰对观测数据的影响。

传播介质的影响及接收器本身和周围环境的干扰[5、6]，给信号检测与识别带来一些困难。如何识别与消除干扰是应用数字地磁前兆资料进行地震预测的基础问题，而如何分离数字地磁资料中的高频与低频信息以及如何识别地震的趋势与短期异常，也是地磁数字化前兆资料分析应用必须解决的问题。因此利用信号处理技术，抑制和剔除干扰，提高信噪比减小各种干扰对地磁数据质量的影响，最大限度保留原始信号，是十分必要的。

小波变换是一种信号的时频分析，它具有多分辨率的特点，可以方便地从混有强噪声的信号中提取原始信号，被誉为分析信号的显微镜[5～7]。噪声通常包含在高频中，因此对实际信号进行小波分解，并对小波分解的高频系数进行门限阈值量化处理后进行小波重构，达到消除噪声的目的，即抑制信号的噪声，在实际信号中恢复真实信号。

本文利用小波分析方法，对泾阳台数字化地磁观测资料消除高频干扰，提取真实地磁变化进行了初步分析探讨。

1 小波变换及资料处理方法

设 ψ（t）为一在 （-∞,+∞）平方可积函数， 即 ψ（t）∈L2（R）， 并满足如下条件：

函数 f（t）∈L2（R）的连续小波变换 DWTa，b定义为

在连续小波变换式（2）中,DWTa，b中尺度因子 (伸缩因子)a和平移因子b(a，b∈R，a≠0)的连续变化的值[9，10]。实际应用中，信号f（t）是离散序列， a与b也需要离散化，成为离散小波变换 DWTa，b。 即

一般采用a=2k。随着k的增加，信号从最高频向低频分解。当时k=0时，信号为采样频率，k=1时将频率二等分，依此类推[3]。

当信号的采样率满足Nyquist frequency（奈奎斯特频率）要求时，用理想低通和高通滤波器将信号分解成频带在0～π/2的低频部分与频带在π/2～π的高频部分。分别得到信号的概貌与细节。对低频部分重复进行下去，直至将原始信号作多分辨分解。

一个含噪声的一维时间序列信号模型的数学表达式[3]：

其中， f（i）为真实信号，e（i）为噪声， s（i）为含噪声的信号。

一般情况下，e（i）近似看作为高斯噪声，通常表现为高频性质，其噪声信号包含在较高频率的细节之中。所以消噪过程可先对信号作小波分解，以门限阈值等形式对小波系数进行处理，然后对信号进行重构即可达到消噪的目的。在 s（i）中恢复出现真实信号f（i）。

采用小波自适应阈值方法确定噪声阈值，通过在不同尺度上选取合适的阈值，并将小于该阈值的小波系数置零或弱化，有效去除随小波分解尺度增大而减小的小波模极大值。而保留大于阈值的小波系数，保留随尺度增大而增大的模极大值，然后用剩余的小波变换模极大值去重构信号，实现噪声信号与地磁信号的有效分离。

2 电源对地磁观测数据干扰的抑制

在观测实践中电源连续稳定的工作是保证正常观测的基础，数字地磁仪器电源工作不正常，可能导致观测数据的断记和数据质量的下降，从而影响观测数据的使用。泾阳台FHD-1核旋磁力仪供电采用交直流双电源模式，市电网停电后直流电瓶自动给仪器供电[4]。图1为2011年3月21日泾阳台FHD-1记录曲线，可以看出11时30分左右开始出现明显的高频干扰，观测室周围环境没有干扰现象，仪器接地良好，探头联接正常。15时30分左右改用直流电瓶给仪器供电，记录曲线高频毛刺消失，因此认为高频干扰与直流稳压电源有关，可能由于FHD-1核旋磁力仪原配的直流稳压电源由于滤波性能下降，对观测记录产生了干扰。其后用东芝笔记本电源适配器 (15 V，电流2A)更换了原直流稳压电源给仪器供电，干扰现象排除。

图1 FHD-1电源干扰（各分量显示存在干扰）Fig.1 FHD-1 power supply interference

3 小波消噪在泾阳台地磁观测数据应用实例

泾阳台地磁记录室东侧约200 m、西侧约400 m，有两条乡间道路，受重型机动车运输所产生的脉冲状干扰的影响，产生脉冲状干扰。一般的脉冲状干扰周期在4～20 s左右。脉冲干扰的幅度与铁磁性物体的磁化率、体积、运行速度以及与观测仪器探头之间距离等参数有关，泾阳台记录到的干扰幅度从几个nT到几十nT都有。图2（a）为泾阳台2011年10月8日地磁观测的原始曲线，图2（b）为采用小波降噪后的结果，图2（c）为原始资料和降噪后结果的残差。资料作小波变换消噪处理。采用此法的理由是该小波有较好的信号自适应性，结果显示能有效的去除部分干扰，信号经重构后，得到相对理想的曲线,与其它正常时段的观测结果保持相似的形态，地磁真实信号保留的很完整。中误差是估算这一波动幅度的可行指标之一[11～13]，计算误差结果显示，降噪后结果的中误差为0.360 5，明显优于原始观测资料的中误差为6.366 1。同样图3给出了2011年4月30日汽车干扰的处理结果，观测数据误差由0.652 6降为降噪后的0.304 6，说明在抑制效果和误差上小波方法是令人满意的。

为进一步分析结果的有效性，图4给出了FHD-1 Z分量2012年7月1日至6日小波抑制噪声对比图，可以看出仍显示了比较好的处理效果。图5给出了距离泾阳地震台约50 km的乾陵地震台观测资料的对比结果，通过小波抑制方法抑制后的数据既不失高频细节信号，在地磁日变形态等长周期信号上也与乾陵台站保持一致。

在处理过程中根据地磁信号每个细节尺度上的波动的大小进行估计是选取该尺度上的阈值的关键。由于小波基函数的选择单一，不能涵盖所有干扰特征形态，小波系数的物理含义也较为模糊[14]，在选择要抑制的小波系数方面存在一定经验性。

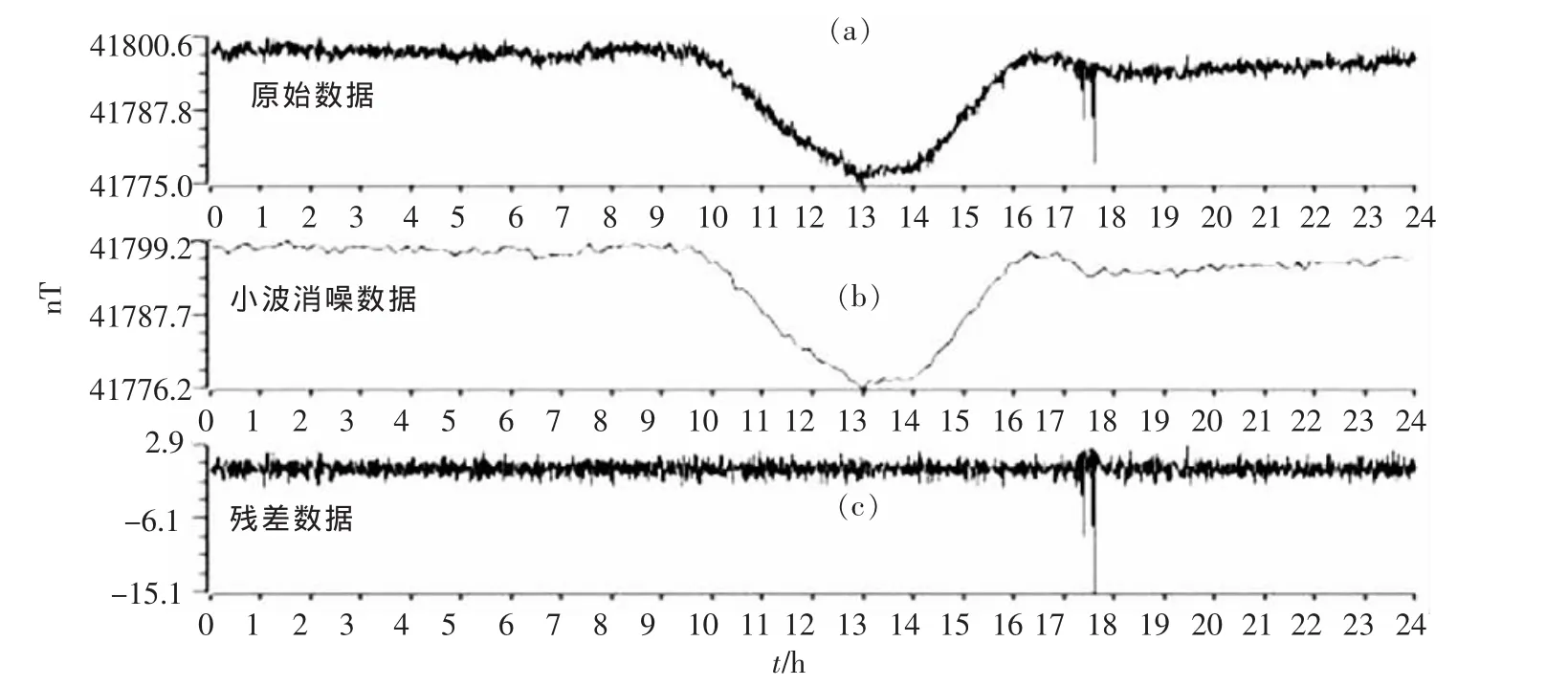
图2 FHD-1 2011-10-08原始图、小波消噪图及其残差值图Fig.2 Original graph,wavelet denoising and their residuals value of FHD-1 on October 8th,2011

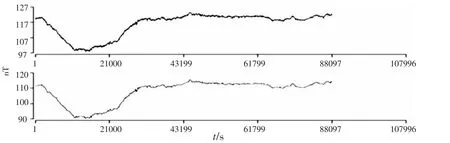
图3 泾阳台GM4 2011年4月30日世界时秒值Z分量原始及抑制汽车干扰对比图Fig.3 Comparison of the original and suppression automotive interference of Z component of the seconds value(World Time)at Jingyang station GM4 on April 30th,2011

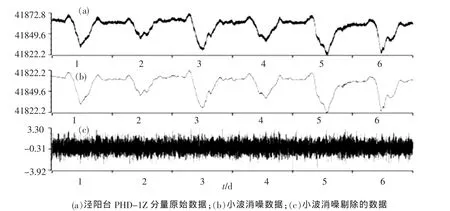
图4 泾阳台FHD-1 Z分量2012-07-01～06小波抑制噪声对比Fig.4 Comparison of noise suppression of Z component at Jingyang station from July 1th to 6th,2012

图5 乾陵台FHD-1 Z分量原始数据图与泾阳台FHD-1 Z分量小波消噪数据对比Fig.5 Comparison of Z component of the original data at Qianling station FHD-1 and wavelet denoising at Jingyang station FHD-1

4 结论与讨论

本文针对泾阳台地磁观测的情况对仪器供电设备导致的干扰可采用高性能的直流稳压电源供电 （或采用直流电瓶供电）消除干扰，对环境噪声干扰，采用小波变换模极大值方法对受干扰的地磁信号进行处理，结果表明：含有噪声干扰的地磁观测数据经过小波变换将低频趋势信号与高频噪声及突变信号很好地分离，Z分量的细节保留充分。因此小波变换对非平稳信号的消噪效果显著,可以用小波变换模极大值抑制方法对地磁观测数据进行预处理，预处理后的结果提高了资料的质量，可更好的研究地磁信号对震磁关系进行探讨。同时对不同的干扰特征，通过具体调试，合理的选取小波去噪阈值是有效的抑制信号噪声的关键。

[1]Jankowski J,C Suksdorff.Guide For Magnetic Measurements and Observatory Practice[M].IAGA.1996.

[2]全国地震标准化技术委员会.GB/T 19531.2-2004地震台站观测环境技术要求第二部分：电磁观测[S].北京：中国标准出版社.

[3]胡昌华，张军波，夏 军，等.基于Matlab的系统分析与设计-小波分析[M].西安：西安电子科技大学出版社，1999.

[4]邢西淳，毛 娟.FHD-1数字化地磁观测系统常见故障维修及电源改进[J].地震地磁观测与研究，2008， 29(6)： 131-138.

[5]Daubechies I.Ten lectures on wavelets[M].CBMS-NSF Regional Conferences Series in Applied Mathematics,1992.

[6]谢凡，滕云田，胡星星，等.地磁台的城市轨道交通干扰的小波抑制方法研究[J].地球物理学报，2011， 54(10)： 2698-2707.

[7]Asimopolos L,Pestina A M,Asimopolos N S.Considerations on Geomagnetic Data Analysis[J].Chinese J.Geophys， 2010， 53(3)： 765-772.

[8]潘泉，孟晋丽，张磊，等.小波滤波方法及应用[J].电子与信息学报，2007，29(1)：236-242.

[9]邵辉成，杜兴信，金学申，等.小波分析在地震趋势预测中的应用[J].中国地震，2000，16(1)：48～52.

[10]邵辉成，杜常娥.中国大陆地震活动的多尺度分析[J].地震学报，2004，26（1）：102-105.

[11]Bruce A G,Gao H Y.Understanding Wave Shrink:Variance and bias estimation[J].Biometrika.1996，83(4)：727-745.

[12]Gao H Y,Gao H,Bruce A G.WaveShrink with semisoft shrinkage[J].StatSci Division of MathSoft，Inc.1995.

[13]Gao H Y.Wavelet shrinkage denoising using the non-negative garrote[J.Journalof Computational and Graphical Statistics.1998， 7(4)： 469-488.

[14]高静怀，朱光明.地震资料处理中小波函数的选取研究[J].地球物理学报，1996，39(3)：392～400.