函数连续的一种新定义

李同荣，崔文艳

(滨州学院 数学与信息科学系，山东 滨州 256603)

0 引言

在研究复杂函数的性质时，通常采用的思路是利用已知性质的简单函数在局部近似代替待研究函数，通过简单函数的性质来得到待研究函数的某些性质.这种用函数在局部的近似值来代替真实值引起的误差称为方法误差［1］.解决方法误差的途径就是需要对近似函数进行不断地修正.如果函数f(x)在某个小区间(a，b) 上有定义，选择一个函数g(x)在(a，b) 上来近似代替，这时就会得到一个误差函数g(x)－ f(x).这样在衡量选择的函数g(x)是否能满足需要时，只需在(a，b) 上考虑误差函数g(x)－ f(x)的绝对值是否能达到足够小，以满足允许的精度.

基于上述思想，本文通过定义误差允许函数引入函数连续的新定义，新定义的给出既丰富了无痛微积分理论，同时也为高等数学教学提供新的参考.

1 主要结论

定义1 如果对于绝对值足够小的h，ε(h)≥0 能达到任意要求的精度，即ε(h)≤指定的精度，则称ε(h)为误差允许函数.

定义2 (函数连续的新定义)设函数y = f(x)在(a，b) 上有定义，x∈(a，b) ，如果f(x)对于绝对值足够小的h，满足一致不等式

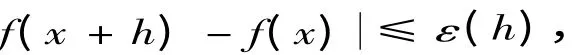
其中ε(h)表示误差允许函数，则称f(x)在x点连续.

为了研究方便，一般可选择| h|的幂函数作为误差允许函数，例如令ε(h)= C| h|，这里C为大于零的某一常数.类似地，可定义函数在某一点左连续和右连续.

定义3 设函数y = f(x)在[x，b)(或(a，x])上有定义，如果f(x)对于绝对值足够小的h≥0(或h≤0)，满足一致不等式

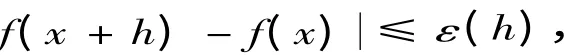
其中ε(h)表示误差允许函数，则称f(x)在x点右(或左)连续.

连续的几何意义 对于函数f(x)，如果用与x + h接近的点x的函数值f(x)近似代替f(x + h)，如果x与x + h足够接近，产生的误差就可以控制在规定的范围之内.

证明首先，对于任意指定的精度ε，满足绝对值足够小的h，有

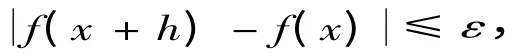
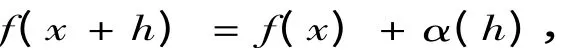
其中α(h)为h→0 时的无穷小量，则对于任意指定的正数ε(h)(精度)，存在h，使得| h |足够小时，

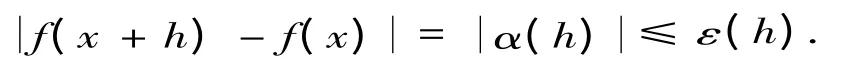
定理2【2－3】函数f(x)在点x处连续的充要条件是f(x)在点x处既左连续又右连续.

证明 由定义2，3 便得.

2 例题

例1【4】证明y = sinx在x处连续.

所以，由定义2 可知，结论成立.

所以，由定义2 可知结论成立.

例3 证明y = ax(a ＞1)在x =0 处连续.

证明 当h足够小，不妨设，当h ＞0 时，一定存在正整数n，使得，此时

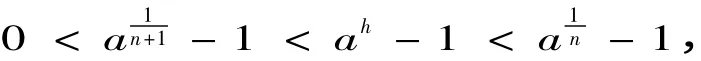
当h ＜0 时，有－ h ＞0，所以，a－h ＞a0=1，此时

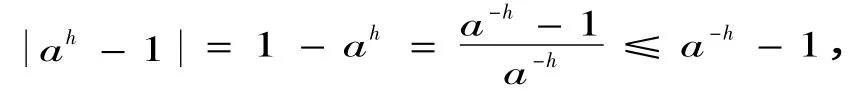
由上边的推导可知

当h =0 时显然成立.

由此，对于绝对值足够小的h，成立一致不等式

由定义2 可知，结论成立.

3 连续与可导的关系

文献［5，6］中依据误差理论曾给出微分的初等定义，下面依据连续的新定义给出连续与可导的关系.

定义4 设函数y = f(x)在(a，b) 上有定义，x∈(a，b) ，如果f(x)满足一致不等式

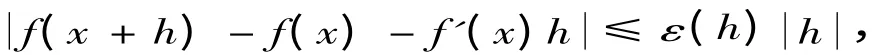
则称f′(x)为函数f(x)在x点的导数.

如果说连续的定义可看作零次多项式的近似，那么可导的定义可看作用一次函数f(x)+f′(x)h来近似f(x +h)的值.这里，不妨看作是对零次近似产生的误差的进一步修正.当然，在一定条件下，这种修正可以继续下去，因此函数在某一点的n阶泰勒展开式可以看做用n次多项式函数近似的结果.

定理3 函数f(x)在x处可导⇒函数f(x)在x处连续.

证明由f(x)在x处可导，即可知

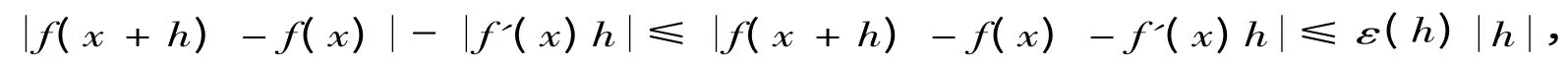
所以

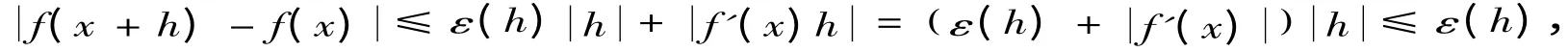
由定义2 可知，函数f(x)在x处连续.

［1］费业泰.误差理论与数据处理［M］.北京:机械工业出版社，2005.

［2］同济大学数学系.高等数学［M］.北京:高等教育出版社，2006.

［3］华东师范大学数学系.数学分析［M］.北京:高等教育出版社，2002.

［4］同济大学数学系.高等数学［M］.北京:高等教育出版社，2011.

［5］林群.微积分快餐［M］.北京:科学出版社，2009.

［6］林群.写给高中生的微积分［M］.北京:人民教育出版社，2010.