《用穷举法设计程序》教学设计

☆高腾

一、教学目标

知识与技能：了解什么是穷举法，了解运用穷举法设计算法的基本过程，能根据具体问题运用穷举法解决简单问题。

过程和方法：通过对实际问题的穷举程序实现过程的观察，发现和归纳穷举算法的一般规律，发展归纳思维，培养独立思考与自主探究的学习能力。

情感与价值目标：了解算法和程序设计在计算机解决问题过程中的重要性，体验将算法变为程序的过程，享受计算机解决问题的快乐，通过对实际问题的解决，体验算法在实际生活中的广泛应用，激发对算法与程序设计的求知欲，形成积极主动的学习态度。

教学重点、难点：

重点：根据具体问题的具体要求来使用穷举法设计算法，并编写相应程序。

难点：学生归纳思维的培养。

二、教学过程设计

1.创设情境，激趣引入

教师活动：我们现在先来回答一道抢答题：甲、乙、丙高考结束后在一起讨论。甲说：“我肯定能考上重点大学。”乙说：“重点大学我是考不上了。”丙说：“要是不论重点不重点，我考上大学肯定没问题。”放榜结果表明，3人中考上重点大学、一般大学和落榜的各一人，并且他们3人的预测结果只有1个是对的。那么，3人中谁考上重点大学，谁考上一般大学，谁没考上呢？

（设计意图：之前的课堂举的都是数学例子，为防止学生“审美疲劳”故采用了逻辑实例来激发学生的学习兴趣，调动学生学习积极性，并为下面的探究创造氛围。）

2.展示问题，引入课题

教师活动：（1）分析人脑解决问题过程并和学生共同完成下表。（2）引入用程序设计来解决问题，要求学生给出算法流程。

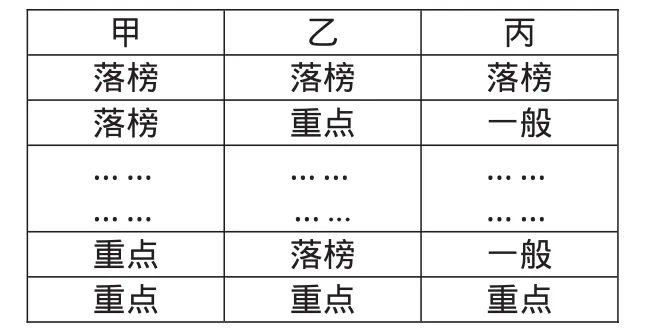
（设计意图：让学生了解人脑是怎么用穷举法来解决问题的，再过渡到通过穷举法编程来解决问题。）

3.师生共同探究

教师活动：逐句分析调试以下程序。

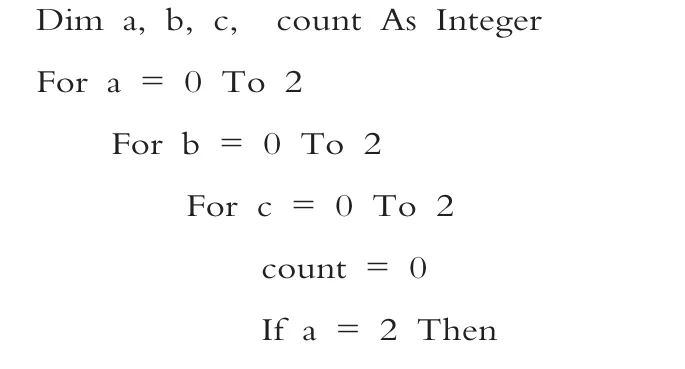
教师引导：在分析了如上程序后，你能发现什么？

学生发现：（1）变量a,b,c存放的是甲、乙、丙的高考结果，分别用0,1,2来表示落榜、一般大学、重点大学3种状态。（2）变量count存放的是3人猜测的结果正确数。（3）此程序的功能是列出3个人所有考试结果，如果满足各不相同且只有1人猜对就输出。

教师总结：此程序的特点是将求解对象的所有可能性都列举出来，然后一个个进行验证是否满足给定条件，若不满足则淘汰，满足则输出。当所有对象都被筛选完后，问题即得到解决。这种算法就是穷举法。

（设计意图：给学生足够的时间观察，学生思考这个过程是无法替代的，最后在教师的引导下总结出穷举法的规律。）

4.知识巩固深化

教师活动：要求学生用穷举法来解决“鸡兔同笼”问题。鸡和兔在一个笼里，共有40个头，100条腿，问鸡有几只，兔有几只？给出以下部分程序代码，与学生共同补充完整。

学生活动：回答问题并对比与自己所写的程序有何不同。

教师引导：（1）上面的程序是否存在不尽如人意的地方，你能修改一下吗？（2）通过以上2个穷举法程序解决问题，你们能总结出一些规律吗？

学生回答：a,b的穷举范围超过需要，可以适当减少以提高程序运行效率。

学生归纳：（1）确定变量个数；（2）确定穷举范围，用for循环实现；（3）穷举规则用if语句实现；（4）尽量减少穷举范围以提高效率。

（设计意图：之前解析法已经有接触到此例，从学生熟悉的例子入手，学生可以在观察过程中发现、归纳并解决问题，并对比穷举法与解析法的差异。）

5.课后实践

问题1：京城某商铺被盗，抓了甲、乙、丙、丁、戊5个嫌犯，可是不知道其中哪几个人是真正的罪犯。不过有确凿的证据表明：（1）如果甲参与了作案，则乙一定也会参与；（2）乙和丙两人中只有一人参与了作案；（3）丙和丁要么都参与了作案，要么都是无辜的；（4）丁和戊两人中至少有一个人参与作案；（5）如果戊作案，那么甲和丁一定也参与了作案。究竟哪些人才是真正的罪犯？

问题2：从1-9这9个数字中取6个填入下面式子中，使等式成立，每个数字每次只能用1次，你能组成多少个等式？

（ ）*（ ）（ ）=（ ）（ ）（ ）

（设计意图：学生在课堂上已经完成了观察、发现、归纳这几个步骤，最后的作业则验证其是否能将所学知识应用到求解实际问题当中，即要求学生应用自己在课堂上归纳总结出来的规律对问题进行求解。）

三、课后反思

本节课有几点收获。

（1）达成率高。学生在掌握了穷举法设计程序的方法后，有运用技术来解决实际问题的迫切愿望，对于课后作业的完成有很大的积极性。

（2）学生分析问题、解决问题的能力得到较大幅度的提高，能将课堂归纳总结到的规律运用到实际当中。比如：课后作业2，学生不仅能合理运用信息技术课堂所学知识来减小穷举范围，甚至还有学生根据排列组合计算出最少的穷举次数，只是因为编程知识所限而无法实现。

（3）采用逻辑题作为课堂实例使得学生对程序设计又有了新的理解，学编程并非只能解决数学问题，不仅活跃了课堂，也留给笔者一个深深的思考——我们究竟需要什么样的教材。

当然本节课也存在不足。本课原本是想全采用逻辑题作为实例讲解的，但是逻辑题作为实例虽好却也存在不足——其穷举范围太小而容易使学生忽视穷举范围影响程序效率这一知识点。如果对其进行修改则又容易导致程序太繁杂不利于学生理解。所以，课堂实例采用了鸡兔同笼这道题作为对知识点的补充与巩固。

[1]张丽.《用穷举法解决问题》教学设计[J].信息技术教育,2007,(6).

[2]余锦波.逻辑的艺术[M].重庆:重庆大学出版社,2011,1.

[3][50]信息技术教材编写组.信息技术[M].福州:福建教育出版社,2012.

[4]王东方.我的计算机绘图课里有故事[J].中小学信息技术教育,2004,（1）.