上海沿海海上搜救预测模型系统的研究和应用

肖文军，堵盘军，龚茂珣，亢兴

（1.国家海洋局东海预报中心，上海 200081；2.华东师范大学河口海岸学国家重点实验室，上海 200062）

1 引言

海上搜救目标漂移轨迹预测的准确性和及时性是搜救工作成功与否的先决条件，对搜救目标漂移轨迹预测方法的研究在保护人民生命财产安全方面具有重要意义。在海洋数值预报不断发展的基础上，以数值预报模型提供风、流、浪等海洋环境预报场，进行搜救目标物漂移轨迹预测的数值模拟手段已成为搜救漂移预测最为有效的途经。

上海北连黄金水道长江入海口，南靠我国第一强潮河口湾杭州湾，是我国航运最为繁忙的海域之一。受如寒潮、浓雾、台风等自然灾害影响及主观因素，海上事故频发，“十一五”期间，仅上海海上搜救中心就组织开展搜救行动893次。随着长江口深水航道的进一步拓深和洋山国际枢纽港的开埠，上海长江口洋山港海域海上运输业及海洋经济的迅速发展，海上作业船只数量和通航密度快速增长，大大增加海上事故的发生概率。

海上搜救预测是根据目标失事位置，类型，以及影响目标运动的海流、风、浪情况，进行随时间变化漂移位置推算。国外海事发达国家对于搜救目标漂移轨迹预测模型研究起步较早，基本已形成较成熟的业务化预报体系，如加拿大的CANSARP[1]、美国的HACSALV[2]、挪威的Leeway等[3]，在搜救工作中发挥了重要作用。国内方面也开展了物质漂移理论方面的研究和搜救漂移预测的研究，刘海峥等[4]介绍了基于蒙特卡洛统计方法的搜救预测理论模型，并举行了理想实验；于卫红等[5]建立了一套根据海流资料和风况推算搜寻范围的方法；陈达森等[6]利用二维海流模式和经验性的风压漂流公式，建立了湛江邻近海域搜救预测模型;姜华林等[7]建立了一个以FVCOM海流模型为基础的海上搜寻区域确定模型进行辽东湾搜救预报试验。国内利用数值模拟手段进行搜救漂移轨迹预测得到一定应用，但考虑的因素较为简单，未考虑海难事故发生时所获取信息的不准确性，且多为单点拉格朗日质点追踪模式，另外还存在系统性不强和缺乏实测案例检验等需改进之处。

本文首先介绍了一种基于蒙特卡洛随机统计理论的海上搜救目标物漂移轨迹预测方法，再基于中尺度气象模式WRF、三维无结构网格海流模式FVCOM和挪威业务化搜救预测模型Leeway，建立了上海沿海高精度海面风场、三维海流数值预报及业务化搜救漂移路径预报模型系统。模型综合考虑了海难事故发生信息的不准确性、风致漂移过程中的多种随机性、海面风场预报误差等多种不确定因素。选取长江口杭州湾海域近年来成功搜救案例进行后报模拟和分析讨论，结果表明所建立的模型系统具有较高的精度，时效性好，具有广阔的推广应用前景。

2 海面物质漂移预测方法

2.1 基本方程

海面物质漂移速度可由下式表示：

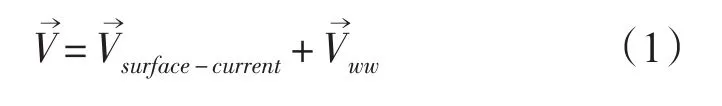
2.2 风致漂移

在实际漂移物的漂移计算中，由于漂移物形状的不规则性，风场的不稳定性、海面状况的复杂性，使风致漂移的速度难以通过理论研究的方法获得可用的结论。因此，通过试验的方法获得风与漂移速度之间的关系成为行之有效的途径。由于漂移物形状的不规则和在流、浪共同作用下物体运动的复杂性，使风作用于漂移物上时，漂移物并不完全沿风向方向漂移，而是与风向有一夹角，称为风致偏移角，将风致漂移分解为沿风向和垂直于风向方向的速度，见图1：

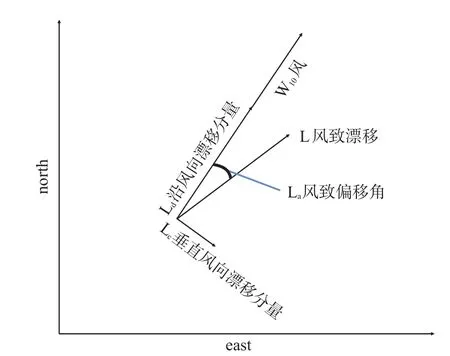
图1 风致漂移分解图

风致漂移量与物体形状和风力大小相关，一般通过实验方法获得。相关大量海上试验表明，分解后的漂移速度Ld、Lc与风速大小有线性相关性[3]，通过最小二乘法可拟合得漂移速度与风速之间的关系可用下式表示：

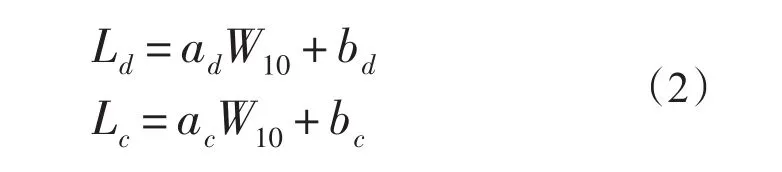
式中：Ld为根据最小二乘法拟合的沿风向的漂移速度，ad，bd，ac，bc为拟合系数,W10为水面10m高度风速。事实上，垂直于风向方向的分量分左侧偏和右侧偏，具有类似的拟合关系式，非对称性漂移物左右侧偏拟合系数不同。

2.3 运动方程的离散求解

利用拉格朗日追踪方法计算任意时刻漂移物位置，由下式给出:

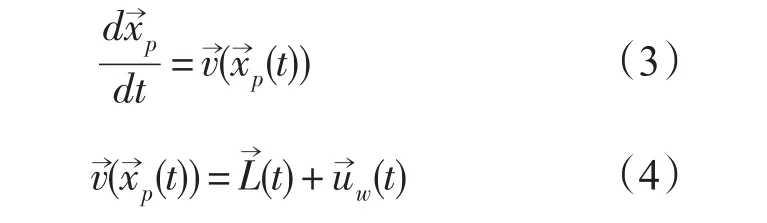
假设物体漂移速度在一个时间步长和在一个空间网格内呈线性变化，在x方向有：

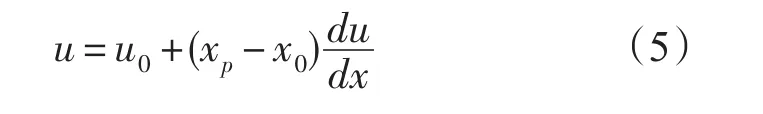
式中：u为x方向漂移速度，u0=u(x0)，为x方向速度变化率，将式（5）代人式（3）并积分得到：

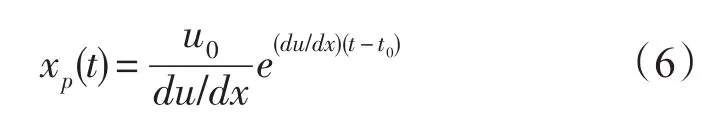
同样地，在y方向可用相同的方法得到：

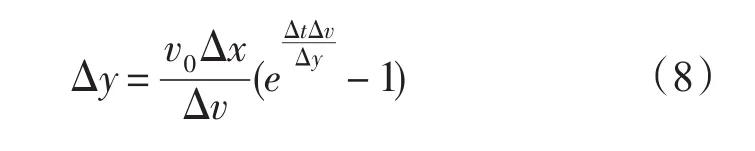
式中：v为y方向漂移速度，对方程式（7—8)求解可得漂移物漂移轨迹。

3 Leeway模式简介

Leeway模式是挪威业务化海上搜救预测模型，模型主要考虑漂移物在表层海流和风作用下的漂移运动。综合了美国和欧洲搜救模型的风致漂移参数共63种，采用速度分解的方法而有别于已有搜救预测模式所大量使用的风偏角方法计算风致漂移。模型根据事故发生情况，在最初可能落水区域和时间段内布设大量漂移质点，考虑漂移过程中各种随机性和不确定性因子，基于蒙特卡洛方法得出具有统计意义的随时间变化的最优搜救区域。同时，Leeway模式还可根据岸界信息和参数控制，计算漂移物触岸。

3.1 确定初始搜索范围

海上事故发生时，搜救部门获得的事故位置、事发时间可能不准确，在进行漂移轨迹预测时，需在不同时刻，不同地点布设初始质点。Leeway模式通过设定事故的发生时段和事发空间范围来布设初始跟踪质点，典型的初始跟踪质点分布有圆形分布（有确定事故时刻和位置信息），直线型分布（无确定事发时间，有确切位置信息，如船舶航行途中人员落水，落水时刻未知的情形）和圆锥形分布（时间空间信息不确切，如已知驶往某海域船舶，一段时间后失去联系的情况）。

3.2 风致漂移方向随机性

LEEWAY模式在预测海面物质漂移时，综合考虑了风致漂移的方向随机性和风场预测误差带来的漂移轨迹变化。在风作用下，海面物质左右侧偏的概率一样，Leeway模式中默认将这种随机性设为相等（也可分别设定其概率），对某一质点设定其为左侧偏，其相邻质点设为右侧偏。以布置500个质点为例，则有250个质点设为左侧偏，250个设为右侧偏。

3.3 风致漂移系数订正

当进行大量漂移质点漂移轨迹计算时，风致漂流速度与风速的线性拟合关系可用一系列线性关系来表示，以去除由于拟合关系误差带来的漂移预测误差。将式（2）的拟合系数斜率a与偏移系数b可看做在一个范围内分布，即：

式中n=1,2...N为设置的线性关系式个数，εn为满足均匀分布的扰动项。考虑风致漂移系数的扰动后，漂移速度与风速的关系见图2。

风致漂移速度L可通过下表所示的9个参数来表示。Leeway模式提供了人员、救生筏、不同船舶共63中不同漂移物的漂移参数，其中人员类参数见表1：

表1 Leeway模式人员风致漂移参数

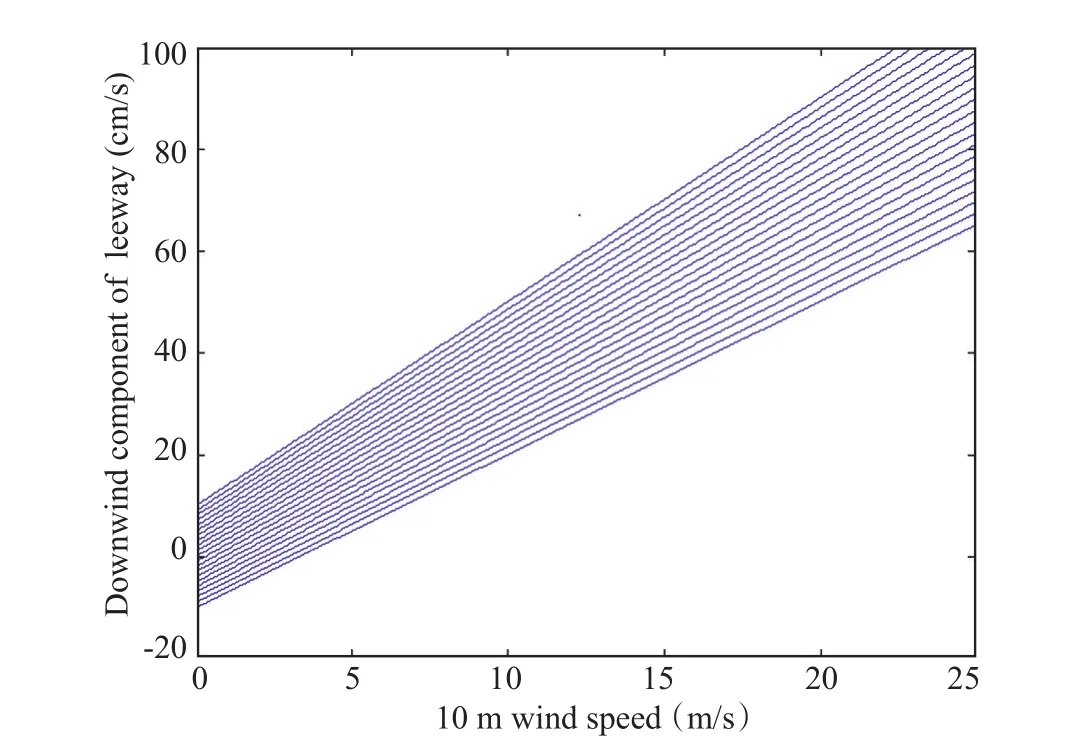
图2 风致漂流速度与风速关系示意图

3.4 风速预测误差

风场预报存在预报误差，为考虑由于风预测误差带来搜救范围误差，模式认为风速预测误差服从平均分布，即：

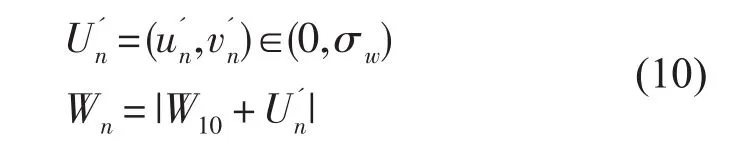
式中σw为风预报标准偏差，根据预测误差统计，在东方向分量和北方向分量均取1.83 m/s，为考虑风预测误差引入的对风速Wn值的修正。风致漂流速度为：

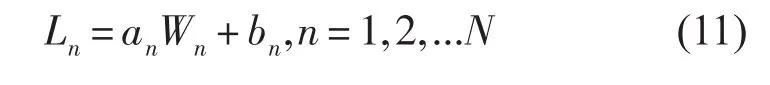
4 上海沿海搜救漂移预测系统的建立

4.1 模型架构

本研究建立了一套完整的搜救目标漂移轨迹预测系统，包括海面风场预报模块、三维海流预报模块、海面物质漂移路径预测模块和业务化运行模块，分别基于WRF、FVCOM及Leeway模型。其中WRF风场预报为一天两次业务化运行（08:00（CST）和12:00（CST））；FVCOM流场预报一天一次业务化运行，利用08:00WRF预报风场作为海面驱动力，预报时效为72h；海洋环境动力场预报模型每天业务化运行，预报结果转换为Leeway模式所用的GRIB数据格式存储，接海上搜救请求后启动Leeway进行海难目标漂移路径预测计算，漂移预报计算耗时小于10 s。同时提供了可人工输入预报风的功能以保证搜救预报系统正常运行，系统流程框架图见图3。

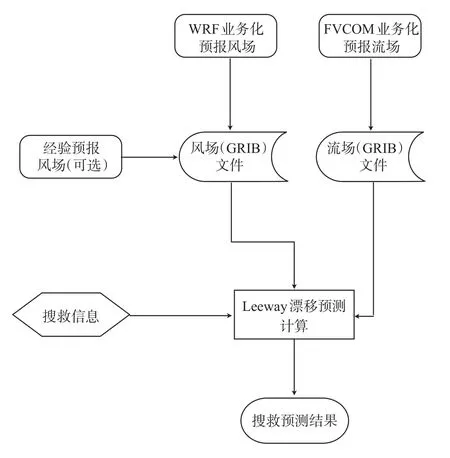
图3 搜救目标预测系统流程框架图

4.2 WRF海面风场业务化预报模块

WRF海面风场业务预报模块是以由美国多家高校及业务预报单位联合研发的WRF中尺度气象模式为基础，结合上海沿海及邻近海域以往天气特征的统计分析，通过对模型局地参数化调整和修正，建立而成的针对上海沿海小区域气象过程的精细化预报系统。预报系统网格分布采用三重嵌套设置，分辨率分别为30 km、10 km、3 km，中区域覆盖整个东海，小区域主要针上海沿海海域。

4.3 精细化三维流场业务化预报系统

上海沿海属于中等强潮海域，海流较强，是海上目标漂移的主要因子，对海流的准确预测是做好搜救预报的基础。上海沿海及邻近海域滩槽交错，地形复杂，为更好地拟合岸界并提高局部海域空间分辨率，选用改进的非结构网格海洋模式FVCOM（Finite Volume Coastal Ocean Model）[8-9]进行潮汐潮流的数值模拟；该模型是一个三维、非结构网格、有限体积法求解的海洋模式，其既有限元法易拟合边界、局部加密的优点，又具有有限差分法计算快速的优点，适用于浅海陆架及近海河口动力环境的模拟计算。

海流模式分东中国海大区域模式和上海沿海模式，计算网格见图4。其中东中国海模型计算区域计算范围115°—134°E，16°—42°N，外海空间分辨率最底约50 km，长江口附近海域最高空间分辨率为1.5 km，上海沿海及邻近海域模型计算区域计算范围120°—124°E，28.5°—32.2°N。涵盖整个长江口、杭州湾及舟山群岛海域，最大网格间距23612 m，最小网格间距62 m。

模式开边界由潮汐调和常数计算水位给出：

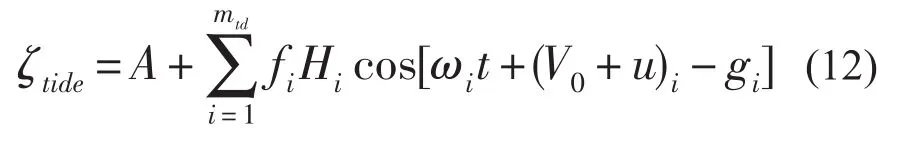
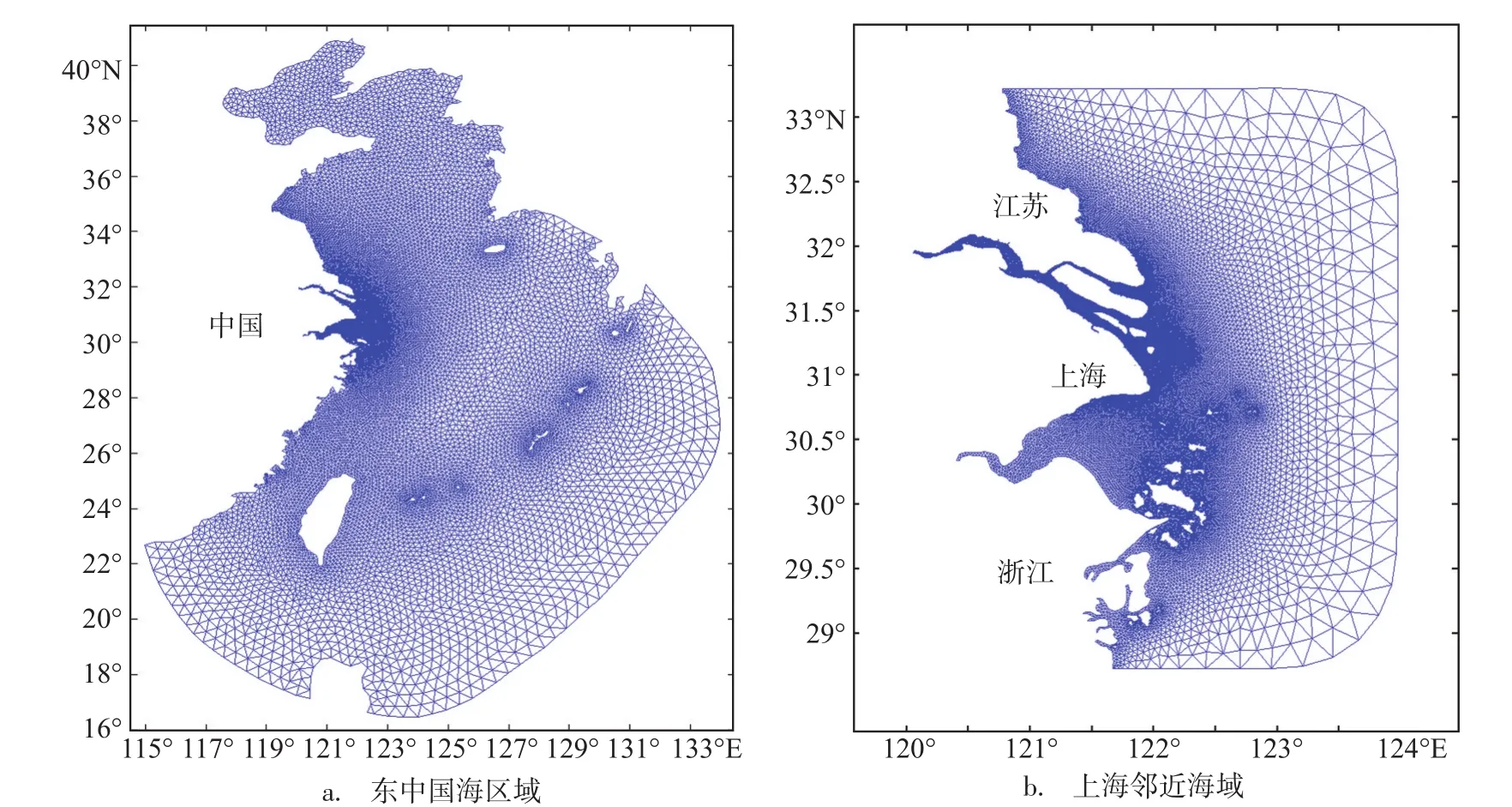
图4 流场模式计算网格

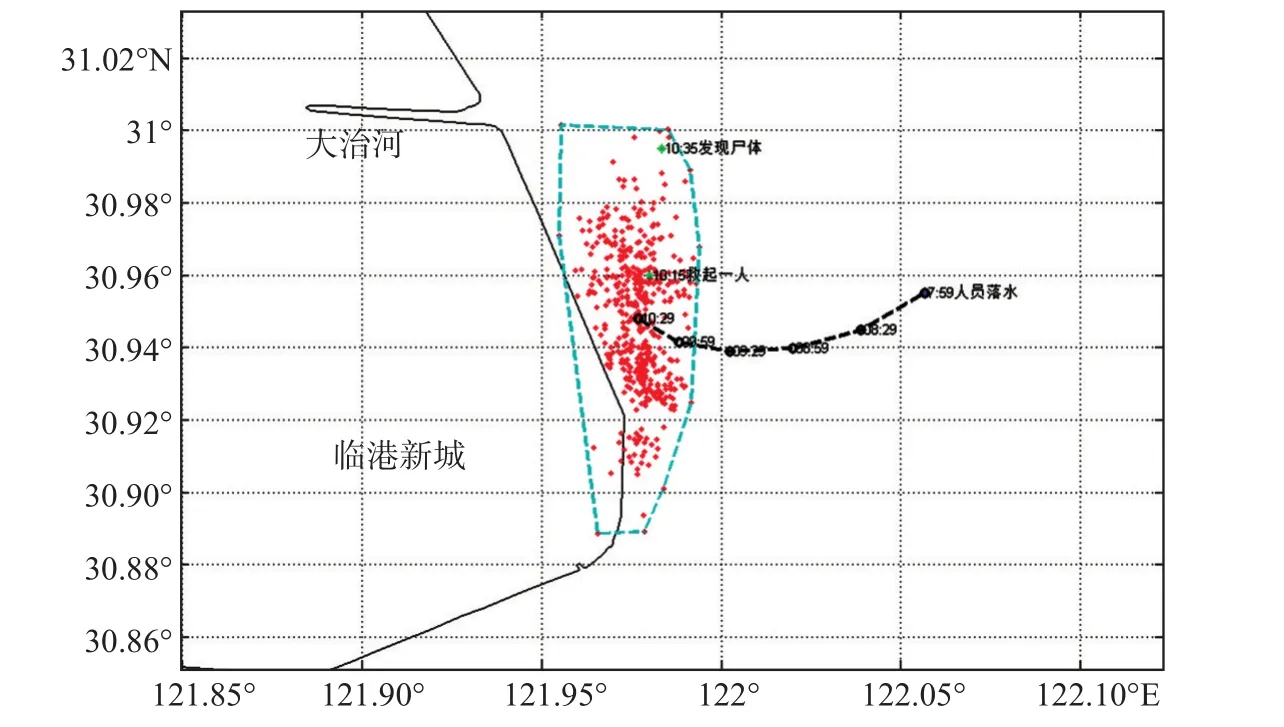
图5 2009年3月搜救预测结果

式中：ζtide为天文潮预报水位，A为平均海面高度， fi,u为由于月球轨道18.6年变化引入的对平均振幅Hi相角V0的订正值， fi称为分潮交点因子，mtd为分潮个数，这里取M2，S2，K1等9个主要分潮，由FES2004全球潮汐模式提供，小区域边界水位由根据东中国海模型结果经调和分析而来的M2，S2，K1等13个主要分潮，通过式(12)计算给出，长江径流取多年月平均值。

4.4 模型验证

风场模型和流场模型均经过观测资料的验证，其中WRF模式经上海沿海海洋站实测资料对比，平均绝对误差为2.6 m/s。FVCOM模式结果经多测站观测资料对比，水位相对误差平均在10%以下，多站表层海流平均绝对误差0.3 m/s。限于篇幅，验证图表从略。

5 搜救案例后报检验与分析

根据东海救助局提供的2004年—2009年搜救案例，对符合模型后报检验需求的案例进行逐一筛选，并进行个例详细分析。以2009年3月一次搜救案例为例，2009年3月某日07∶59，在南汇东滩附近有船进水沉没，船员落水。事发时该海域5—8 m/s东风转东南风。在搜救过程中成功救起船员一名，找到遇难人员一名。由于记录中未提及是否穿救生衣，模型搜救目标设为未知状态人员。与其他“人员”类型的风漂参数相比，未知状态下的人员漂移参数其斜率项介于其他几种类型之间，风漂系数扰动项为12，在几种人员类型中最大。初始搜索质点为半径为2 km的圆形分布，初始漂移质点设为500个，计算时间步长设为15 min，模型输出时间间隔为30 min。当日10∶15，在南汇近岸成功救起船员一名，10∶35在大治河外发现遇难人员一名。预测结果见图5。

根据模型计算结果和成功搜救到的人员位置可看出，搜寻到人员位置位于预测范围内，与预测中心点相距5.29 km。从图中可以看出，由于受近岸沿岸流作用，搜救范围呈沿岸的长条状分布，而图中出现在岸上的一些预测点则是由于全球GSHHS岸界数据尚未包括新围垦岸界的缘故。

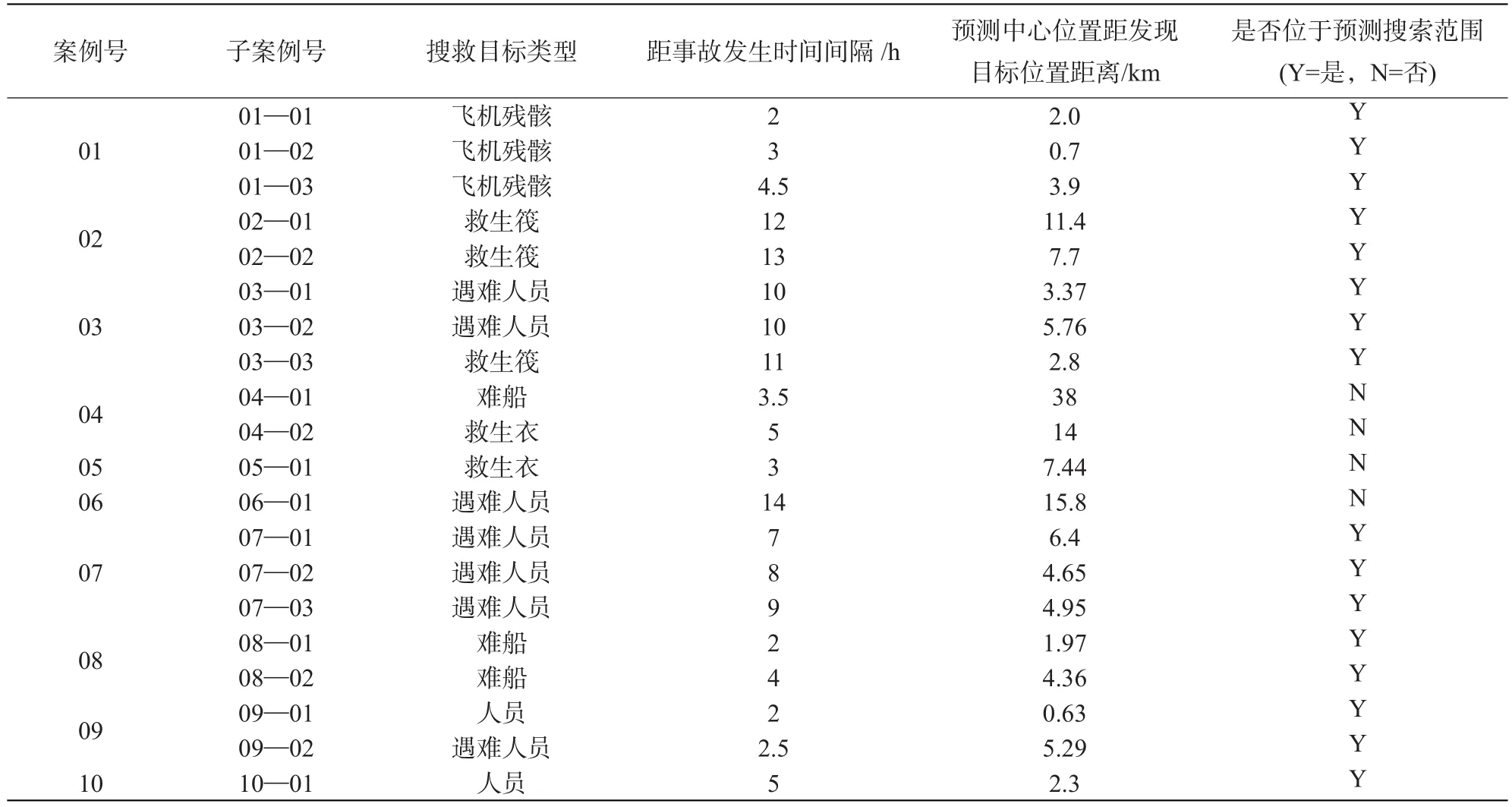
表2 搜救案例模拟结果

表3 分时段统计预测中心位置与找到目标位置距离

通过对2004年—2009年以来的历史搜救案例信息进行整理，选取成功案例进行模型对比检验，以进一步验证上海沿海海上搜救预测模型系统的可靠性，模型结果与搜救结果对比见表2。

根据找到目标距离海难事故发生时间的不同，分2—6 h，6—10 h，10 h以上分别统计模型预测中心位置与找到目标位置的距离，结果见表3。

从案例和模拟结果的分析来看，搜救目标漂移轨迹呈现下列特点：

（1）海面物质漂移随机特性

对同一起海难事故，同段时间内在不同地方发现类似漂移目标其位置可能相差较大，如案例07和案例09,在相差1 h左右的时间发现的两名人员相距超过了6 km。由于搜救目标漂移随机性的存在，漂移时间越长，带来的不确定性越大，搜救预测范围也随之扩大，带来搜救难度的增加。

（2）风对不同种类漂移物影响分析

海面漂移物受海流和风的作用，对不同类型的漂移物，起主要作用的动力因子不一样，例如竖直状态下的人主要受海流作用，受风作用较小（风漂流拟合关系式其斜率项为0.48），而对帆板船来说，主要受风的作用，风漂流拟合关系式其斜率项达6.54，而如救生衣类的轻型海面漂移物，风对其漂移起着主要作用。

6 结论

本研究以上海建设国际航运中心对于海上航运安全保障的重大需求为出发点，通过构建长江口邻近海域高分辨率WRF气象模式、FVCOM潮流模式和搜救目标漂移轨迹计算模式Leeway，集成创新建成国内首个以上海沿海及邻近海域为重点，基于蒙特卡洛随机统计方法的搜救目标漂移轨迹集合预报数值预报模型系统。通过对近年来发生在长江口邻近海域的海难事故及搜救资料进行分析和模拟，检验表明所建立的模型系统操作方便、时效性高，验证了Leeway漂移模型在长江口的适用性。

由于国内的一些救生筏、船舶与国外相比，其形状、大小存在一定差异，在直接引用相关参数时需要引起注意，在今后的研究中，还需对国内某些特有的搜救目标开展必要的现场实验，找出其漂移规律。同时，Leeway模型主要考虑了风驱动力的预报误差和风致漂移随机性，在海流较弱，风为主要驱动力的海域中更加合理，而在中国大部分沿海海域，海流较强，海上搜救预测时还应考虑到海流预报误差所带来的漂移轨迹误差。

[1]Fisher and Oceans Canada,Canadian Coast Guard.CANSARP User Manual[M],Canada,Fisheries and Oceans Canada,Canadian Coast Guard,2009.

[2]Allen A A.Leeway Divergence Report.Report CG-D-05-05[M].USA,US Coast Guard Research and Development Center,2005.

[3]Øyvind B,Allen AA.An operational search and rescue model for the Norwegian Sea and the North Sea[J].Journal of Marine Systems,2008,69:99-113.

[4]刘海峥,赵怀慈,赵春阳.基于Monte Carlo方法的搜救区域预测算法[J].船海工程,2010,39(1):132-135.

[5]于卫红,贾传荧.海上搜救中搜寻区域确定方法研究[J].中国航海,2006,2:34-37.

[6]陈达森,严金辉,毕修颖.湛江毗邻海域流场模型在海上搜救中的应用[J].热带海洋学报,2008,27(1):16-21.

[7]姜华林,孙昭晨,李黎,等.基于蒙特卡洛方法的海上搜寻区域确定模型[J].水道港口,2011,32(4):285-290.

[8]Chen C,Liu H,Beardsley R C.An unstructured,finite-volume,three-dimensional,primitive equation ocean model:application to coastal ocean and estuaries[J].Journal of Atmospheric and Oceanic Technology,2003,20:159-186.

[9]肖文军,堵盘军,邬惠明.东海区三维风暴潮数值模式的建立和应用[J].海洋通报,2010,29(s):28-33.