流线数值模拟中的无效网格处理方法
王 宇 李治平
1.陕西延长石油(集团)有限责任公司研究院,陕西 西安 710075;2.中国地质大学(北京),北京 100083
0 前言
流线模拟技术能将三维模拟模型转化为一系列的一维流线模型,实践表明流线方法是一种快速有效的数值模拟计算方法,流线模拟技术能更好地认识地下流体的分布、运移,改善油田开发效果和提高油田最终采收率[1]。在实际油田开采过程中,油田内往往存在无油非连接区域,有些局部区域为局部断层影响的水动力滞留区或为泥岩,此时在油藏数值模拟过程中对应为不可流动区域,网格化后即为无效网格。无效网格的存在会影响流线数值模拟的压力场计算以及流线追踪过程,导致流线数值模拟失败。
另外,油藏形状各式各样,进行网格划分后往往是非规则形状,形成统一的差分过程,对角矩阵过程复杂,而将油藏划分为规则的矩形,对其内部流体不可流动区域按无效网格处理,形成流程化计算,计算过程更为高效。因此,无效网格研究对于流线数值模拟计算具有重要意义。
1 压力数学模型与无效网格的处理
1.1 压力方程
在二维两相的前提下,考虑流体与岩石的压缩性,忽略重力及毛管压力,考虑维数因子和产量项,根据达西定律、质量守恒定律以及流体状态方程可得到二维两相流数学模型[2-3]:

式中:K 为油藏的绝对渗透率,D;μo、μw分别为油、水相黏度,Pa·s;kro、krw分别为油、水相的相对渗透率,无因次;p 为油藏压力,MPa;qo、qw分别为油、水相在单位时间、单位体积岩石注入(或采出)的质量流量,kg/(m3·s);ρo、ρw分别为油、水相的密度,kg/m3;So、Sw为油、水相饱和度,%;φ为孔隙度,%;t 为时间,s。
由式(1)~(2)可得到压力控制公式[4-5]:
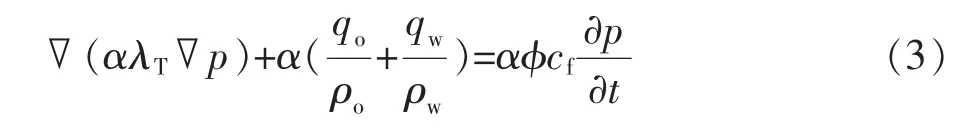
对式(3)五点隐式差分,把引起非线性的系数作显式处理后得:

如果把式(4)写成矩阵的形式,即AU=g,A称为该线性方程组的系数矩阵,矩阵结构为五对角形式。如果在某一个网格处有井存在,则把它作为点源或点汇来处理,在对网格建立的差分方程中增加一个产量项。
1.2 差分过程无效网格的处理方法
差分过程无效网格的处理方法有三种。第一种方法是直接计算法,对研究区域网格化处理后,只对有效网格节点差分,而与无效网格相连的有效网格得到差分方程后,求解五对角矩阵方程,此方法会因无效网格数及所处模拟区域位置的变化而需重新进行差分和计算五对角系数矩阵,这种方法无法形成统一、有规律的计算方法,尤其不适应程序化、软件化数值模拟。
第二种方法是镜像反映法[6],将无效网格作为周边与其连接的可流动网格的镜像,使其压力等于周边网格的压力,此时镜像网格在计算过程中无流体发生渗流。块中心网格见图1,从图1 可看出,对无效网格i、j 点差值后,采用镜像反映法处理时,可使此时在i+1/2,i-1/2,j+1/2,j-1/2 网格边界处,无流量通过,(i,j)网格内无流量变化,这时(i,j)网格即为无效网格。

图1 块中心网格
镜像反映法尽管不需随着无效网格的改变而重新计算方程的系数矩阵,能形成一个统一的算法,但需要每一个时间步长内设置无效网格的压力,使之与周边网格压力相等,计算过程繁杂,模拟过程的不断赋值,大大降低了计算效率。
第三种方法是网格设置法,可直接设置无效网格的φ及Ki,j为0,即无效网格,此时网格就成为无效网格。因综合压缩系数为式(3)右边的综合压缩系数意义已不适用,应以展开形式带入公式,以避免存在无意义情况。另式(4)中的λTi+1/2等系数,均按“上游权”的取值原则。由于计算过程中网格的渗透率取“上游权”原则,对于无效网格则不需要此判断过程,只要确定无效网格边界渗透率值为0,见图1。(i,j)网格为无效网格点,其边界渗透率kri+1/2、kri-1/2、krj+1/2和krj-1/2均为0。
由于无效网格的存在,对应网格点的渗透率为0,差分后的五对角矩阵行列式为0,无法求解方程组,因此需要将矩阵中为0 的行、列除去。压力方程求解完毕后,得到对应网格在tn+1时刻的压力值,即压力场。此方法可直接将不规则形状油藏划为矩形油藏进行计算,并形成了统一的系数矩阵计算方法,其系数矩阵计算规律简单,计算速度快。
2 流线数学模型与无效网格的处理
流线数值模拟方法作为新兴的数值模拟技术方法,与传统的数值模拟方法相比有很多优点,能为生产实践提供指导和技术支持。当模拟区块外部、内部存在不可流动区域时,无效网格处理方法能够有效解决数值模拟过程中的压力求解、流线追踪以及流线饱和度计算等因存在无效网格而出现的问题。
2.1 流线追踪与无效网格的处理
在存在无效网格的流线数值模拟中,流线应避开无效网格区域。Pollock 提出的追踪流线轨迹方法是在网格系统中压力场已知的情况下,应用达西定律建立流体真实流动速度场,然后在此基础上追踪流线。
考虑二维情况,根据达西定律计算每个网格界面上的速度分量[7-8]:
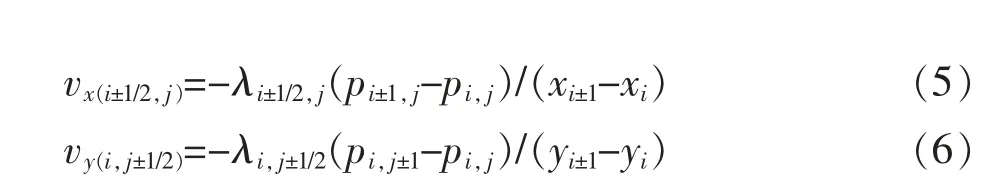
图2 中采用Pollock 方法进行流线追踪。x 方向的速度定义为:

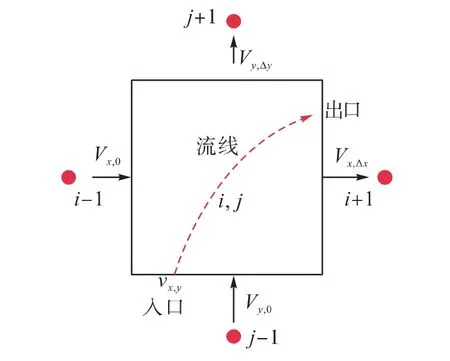
图2 流线穿过网格过程
对于无效网格,应没有流体流入或流出,网格边界封闭,无效网格边界不存在流体速度,因此无效网格边界速度应取为0。
为了避免速度为0 而出现无意义情况,可将无效网格边界速度在一定精度下取值无穷小,这样可模拟流线在遇到无效网格时的情况,此时流线流动到无效网格边界的时间无穷大,即不可到达。完整的流线追踪过程可得到流线流动的完整路径[9]。
2.2 流线饱和度模型与无效网格处理
要采用流线方法求解生产阶段的渗流数学模型,首先要将基于网格的二维或三维模型转化为沿流线的一维模型。
定义沿着流线的传播时间(Timeof Flight,TOF)[10]为:,处理后最终得到:即流线饱和度方程。
无效网格内不存在流体流动、变化,因此流线不经过无效网格,饱和度方程仅跟流线所经过的网格有关,因此无效网格不影响其他网格饱和度的计算。
3 应用分析
选取长庆定边姬塬油田罗1 井区长8 油藏内的4口采油井、1 口注水井作为应用对象,根据所研究区域储层主要参数及储层流体特性资料作为流线数值模拟的基本参数。
网格系统采用块中心网格系统,纵向不划分网格,平面上不考虑储层的非均值性,将平面划分为19×19×1 网格系统。无效网格区域分布在3 个区域。模拟区域中央为注水井,4 口采油井分布在储层四边,无效网格分布在下面三个部分,分别为左下边的单个无效网格、2 个连接无效网格以及右下边6 个相连的无效网格。
根据前面的数学模型及第三种无效网格处理方法,编写了流线数值模拟计算程序,模拟3 月后,得到了模拟区域1 注4 采井网形式的流线分布特征,见图3。
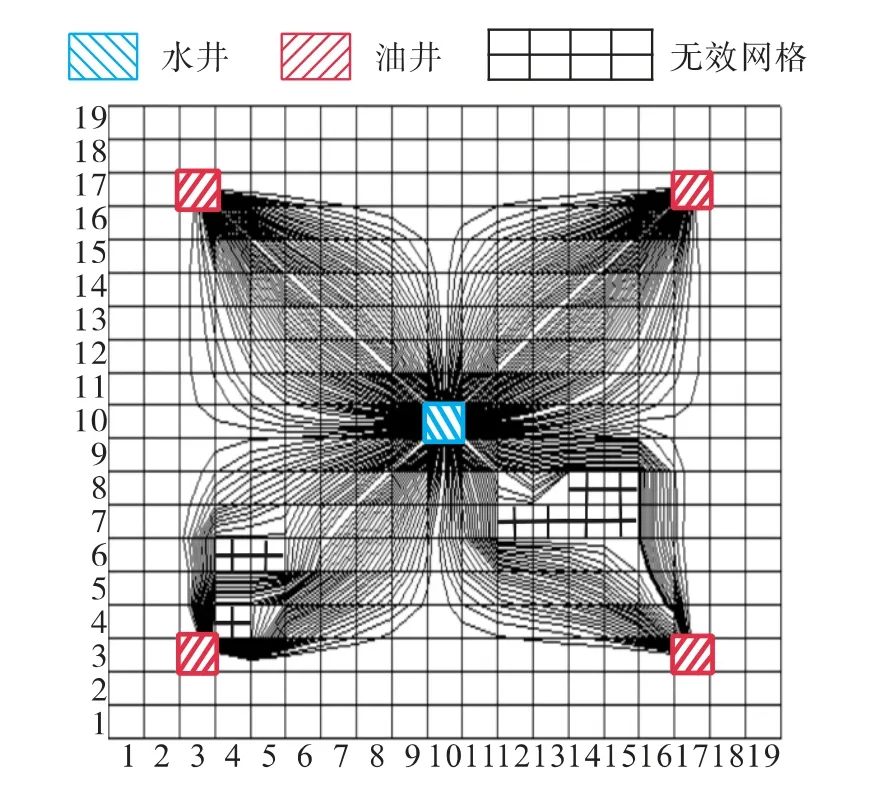
图3 存在无效网格流线分布
从图3 中可以看出流线从中间1 口注水井出发,流向周边的4 口生产井,流线碰到无效网格区域会明显出现变化,而三部分不可流区域无流线通过,流线绕过不可流动区域,流向了注水井,流线明显改变了流线原有形状,证明了无效网格处理的有效性及合理性。
由于不可流动区域的存在,靠近不可流动区域,流线分布较密,而流线分布密集地区反映了注水流量大,驱油效果好。
4 结论
a)差分过程无效网格处理方法中,网格设置法计算最为简便,方程系数矩阵算法最容易得出,直接计算法无法形成统一、有规律的计算方法,尤其不适应程序化、软件化数值模拟;镜像反映法计算过程繁杂,模拟过程的不断赋值,大大降低了计算的效率。网格设置法弥补了直接计算法和镜像反映法的不足,既形成了统一的系数矩阵计算方法,又有相对较快的计算速度。
b)网格设置法可将不规则形状油藏按规则的矩形油藏进行数值模拟计算,并形成统一的系数矩阵计算方法,简化了模拟计算过程。
c)Pollock 的追踪流线轨迹方法在进行追踪流线轨迹过程中,因无效网格的存在,在处理网格边界时,会影响流线变化,改变饱和度的计算过程。
d)应用无效格处理方法可解决含启动压力梯度的情况下油藏动边界问题,因油水两相方程动边界很难给出解析形式,所以需要应用数值方法求取确定,通过小时间步长计算确定动边界范围,再将动边界外部确定为无效网格,这样可解决因启动压力梯度的存在,动边界外部流体渗流速度为负的情况。
[1]Batycky R P A.Three-Dimensional Two-Phase Scale Streamline Simulator[D].Department of Petroleum Engineering,School of Earth Science,Stanford University,1997.
[2]刘慧卿.油藏数值模拟方法专题[M].东营:石油大学出版社,2001.Liu Huiqing.Topic of Numerical Simulation of Oil Reservoir[M].Dongying:China University of Petroleum Press,2001.
[3]郭鸣黎,程东风,李大勇.文25 东复杂断块油藏剩余油分布研究[J].江汉石油学院学报,2003,25(3):82-83.Guo Mingli,Cheng Dongfeng,Li Dayong.Remaining Oil Distribation of Complex Fault Block Reserovir in the East of Block Wen 25[J].Journal of Jianghan Petroleum Institute,2003,25(3):82-83.
[4]尹 虎,王新海,刘 洪,等.考虑启动压力梯度的页岩气藏数值模拟[J].天然气与石油,2012,30(4):43-45.Yi Hu,Wang Xinhai,Liu Hong,et al.Numerical Simulation of Shale Gas Reservoir Considering Startup Pressure Gradient[J].Natural Gas and Oil,2012,30(4):43-45.
[5]王 平,姜瑞忠,王公昌.高含水期水驱状况影响因素数值模拟研究[J].天然气与石油,2012,30(4):36-38.Wang Ping,Jiang Ruizhong,Wang Gongchang.Numerical Simulation of Factors Affecting Water-Flooding in High Water-Cut Stage[J].Natural Gas and Oil,2012,30(4):36-38.
[6]韩大匡,陈钦雷,闫存章.油藏数值模拟基础[M].北京:石油工业出版社,1993.87-93.Han Dakuang,Chen Qinlei,Yan Chunzhang.Fundamentals of Numerical Reservoir Simulation[M].Beijing:Petroleum Industry Press,1993.87-93.
[7]Portella R C M,Hewett T A.Fast 3-D Reservoir Simulation and Applications Using Streamlines[C].SPE 39061,1998.
[8]姚 军,吴明录,戴卫华,等.流线数值试井解释模型[J].石油学报,2006,27(3):96-99.Yao Jun,Wu Minglu,Dai Weihua,et al.Streamline Numerical Well Test Interpretation Model[J].Acta Petrolei Sinica,2006,27(3):96-99.
[9]Batycky R P.Martin J B,Marco R T.A 3D Field Scale Streamline Simulator With Gravity and Changing Well Conditions[C].SPE 36726,1996.
[10]吴明录,姚 军.不规则污染井的流线数值试井解释模型及其应用[J],新疆石油地质,2009,60(3):373-375.Wu Minglu,Yao Jun.Streamline Numerical Well -Testing Interpretation Model for Irregularly Contaminated Wells with Application[J],Xinjiang Petroleum Geology,2009,60(3):373-375.

