多频多幅振动压路机的参数优化及其偏心块组的设计
但斌斌,邬俊惠,容芷君,周 鼎
(武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081)
1 引言
常规振动压路机的振动频率和名义振幅是固定,但是在压实作业中,土壤在不同环境下,其刚度和阻尼是截然不同的,同时土壤在振动压实的不同阶段,自身的刚度和阻尼也是变化的,一般分为塑性阶段,弹-塑性阶段,相对刚性阶段[1]。多频多幅压路机作业时,振动轴上的一组偏心块高速旋转以产生离心力,强迫振动轮对地面产生很大的激振冲击力,形成冲击压力波,向地表内层传播,引起被压层颗粒振动或产生共振,最终达到预期的压实目的。对于不同的压实材料和铺筑层厚度,应该采用不同的振动频率和振幅.从而产生适当的激振力以及压实能量,以达到最佳的压实效果[2]。着重设计一种满足多频多幅的振动式压路机,对其频率和振幅进行优化设计,并设计一组偏心块,利用其组合关系,应对不同工况下的最优压实效果。
振动压路机的工作装置在振动压实时,一方面是振动轮对被压实材料的冲击力越大,压实效果就越好:但从另一方面讲,强烈的振动有损于机器零件的使用寿命和司机的身体健康,因此要求振动压路机的上车振动能量尽量的小,这就是振动压路机上设置减振系统的目的[3]。因此,压实与减振,这一对相互矛盾的设计指标,成为了压路机设计的关键技术。
根据文献分析结论,在减振器的刚度阻尼一定时,压路机的减振性能主要由工作振幅和工作频率决定。同时这二个参数也决定了振动压路机的激振力。将这二个参数作为设计变量,利用优化设计方法,对组研制的TZ4000 系列多频多幅振动压路机的关键设计参数进行优化分析,实现基于压实效果最优和驾驶舒适性最佳两个目标的压路机相关参数设计。最后设计一组偏心块,实现多种环境下土壤的最优压实。
2 振动系统分析
2.1 多频多幅振动压路机设计原理
利用变频器实现对振动频率的调节,变频器与振动电机连接,振动电机带轮与振动带轮之间通过皮带传动,通过调节变频器的频率实现电机转速的调节,从而使振动轴转速变化。多频多幅振动压路机设计的关键问题是实现压实的多幅,由于振动压路机主要利用垂直方向的激振力来压实土壤,TZ4000 型压路机主要采用垂直分布的三根振动轴分别安装三个偏心块,通过偏心块的组合关系来提供不同的激振力,从而实现振动压路机的多振幅。扇形偏心块的设计结构,如图1 所示。偏心块组布置的基本简图,如图2 所示。为了保证振动的平稳型,一般将中间的振动轴称为主振动轴,其偏心矩是三者中最大的,该组偏心块能通过组合关系能合成6 中不同的振幅。
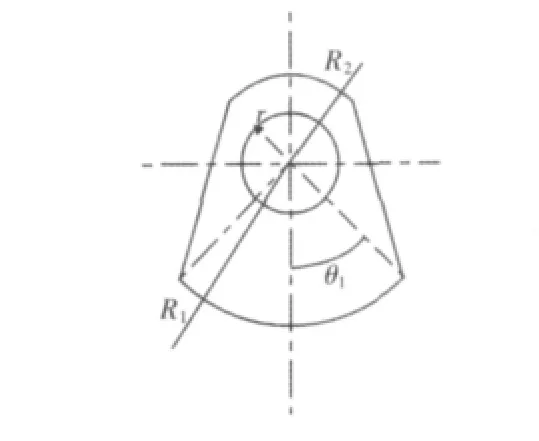
图1 偏心块结构简图Fig.1 Eccentric Block Structure Diagram

图2 偏心块组的结构简图Fig.2 Eccentric Block Group Structure Diagram
2.2 振动压路机关键参数
2.2.1 压路机名义振幅
通常情况下振动压路机的振幅指的是压路机的名义振幅,压路机的名义振幅即决定了压路机由振动偏心块提供的激振力大小。而振动压路机的工作振幅是一个变化的值,与其名义振幅和土壤的性质密切相关,希望其值在可取范围内尽量大,以保证压实的能力,但是振动轮振动过大,不但会出现过压实现象,还会导致上车的振动剧烈,严重影响驾驶舒适度。
名义振幅计算方法,A0=T/M,M 为下车质量,T 为静偏心距,因此名义振幅主要由偏心块提供的偏心矩决定。
2.2.2 压路机激振频率
不同的土体,其固有频率是不同的,根据共振原理,只有当激振频率接近或等于土体的固有频率时,压路机压实效果最强。为取得最佳压实效果,对于不同的土体,振动压路机激振频率是不同的。试验表明,振动压路机激振频率应比土体固有频率稍高一些,同时激振频率也不能选的过高。
同时,机架和振动轮系统有两个共振频率。当振动频率在二阶固有频率以上时,机架的位移逐渐减小且平稳。当振动频率在二阶共振区以内时,虽然在理论上机架、振动轮的位移都很大,有利于压实,但机架很有可能与振动轮产生共振,这会导致机架振动更为急剧,严重影响减振效果。所以,振动频率不但影响振动压路机的压实效果,对振动压路机减振性能也有较大的影响。
2.3 振动系统运动学分析
如图所示为振动压路机的二自由度数学模型,对振动压路机的运行学分析,以实验室研制的TZ4000 型为例,由于理论分析,这里做一些模型假设,首先将减振器刚度为K1,阻尼为C1,其阻尼近似作为线性阻尼,由于土是具有一定刚度的弹性体,其刚度为K2,阻尼为C2,阻尼为线性阻尼。其次把振动压路机的上、下车的质量简化为具有一定质量的集中质量块,上车质量为m1,下车质量为m2,随土振动的质量为m3。压路机工作时一般情况下紧贴土壤表面,不会跳离地面,所以把压路机的振动系统看作是二阶系统[4],如图3 所示。
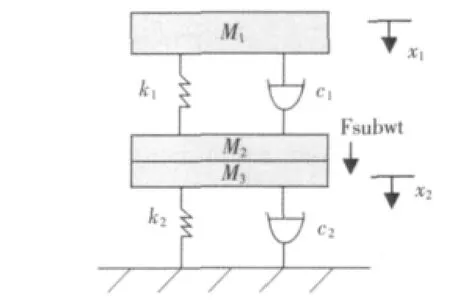
图3 二自由度运动学模型Fig.3 Two Degree of Freedom Kinematics Model
其运动学方程为:

式中:F,ω—激振力和激振频率;x1,x2—上车和振动轮位移;F—偏心振子提供偏心力,即激振力;m—偏心块质量;r—偏心距。
设其他参数为已知,根据上式可解微分方程求得x1,x2。

其中,A=m2m1ω4-m2k1ω2-c1c2ω2-k1k2-m1k1ω2;
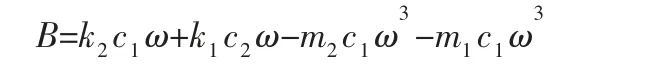
振动压路机下车(振动轮)对地面作用力Fs的大小不仅与振动压路机本身的振动参数有关,而且也与被压实土的刚度k2和阻尼c2有关。Fs可表示为:

前者与振动压路机的瞬时振幅和土的刚度有关,后者与振动压路机振动速度和土的阻尼有关。所以,振动压路机对地面的作用力大小与土的物理特性有着密切的关系。无阻尼状态下振动系统的一阶、二阶固有频率ω1、ω2分别为:

3 偏心块组的设计
多频多幅振动压路机利用放置在一根或多根平行振动轴的偏心块组,根据其组合关系来提供不同的偏心矩,从而实现压路机的多个名义振幅,振动频率主要由振动电机的转速调整来实现,现在的电机。当设计n 个偏心块时,可以选择的振幅组合有:

TZ4000 系统振动压路机采用3 个组合偏心块,可提供六种名义振幅,对常见土壤的参数进行分析,根据上述优化计算模型求的名义振幅和频率,选择合适的偏心块组,一般偏心块组数量为2~5,例如设计三个偏心块组,X=[X1,X2,X3]T,根据组合关系可生成(X1,X2,X3,X1+X2,X1+X3,X2+X3,X1+X2+X3),并使这些组合的偏心距值尽可能满足计算的名义振幅范围。
根据优化模型计算出振幅,频率结果,对其进行数学分析处理,在采用三个偏心块的条件下,优选六个代表性的幅值与频率结果,设其处理幅值的结果为(A0,A1,A2,A3,A4,A5)并对这六个幅值排序,设X1<X2<X3,则可得到这六组偏心块组的排序,根据数据拟合方法,按最小二乘方的原则,来求的[X1,X2,X3]T。
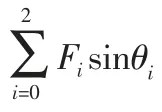
4 算例
以实验室TZ4000 系统振动压路机样机为例,上车质量没m1为1800kg,振动轮质量m2为2200kg,通过对振动轮土壤系统的被测性能与等效参数系统所算得的振动性能的分析比较,以10%的振动轮分配质量计入m2的数值。随振土壤质量一般为振动轮质量的220kg。由于本压路机的柴油发动机放在前端,因此分配在前轮的重量F0约为2500kg。根据国内外文献资料,常见压实材料的刚度阻尼,如表1 所示。
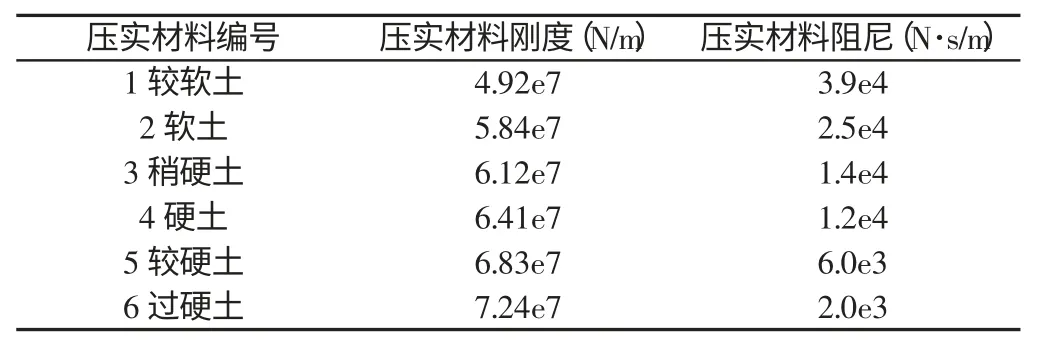
表1 常见压实材料的刚度阻尼列表Tab.1 Stiffness Damping List of Common Compaction Material
利用式(12)算法求解得到最优的振幅和频率,如表2 所示。
5 结论
多频多幅设计的难点在于提供多振幅的偏心块的选择与设计,利用一组偏心块来提供多偏心矩,从而实现多振幅的压实振动。为多频多幅压路机在不同工况下工作时(随振土壤的刚度和阻尼不同时),调整工作频率和振幅参数提供了理论依据,在设计压路机时,同时保证压实最优和减振最好两个目标的前提下,提供一组优化的偏心块。以本课题组的TZ4000 系统振动压路机样机为例,运用上述优化模型对其参数进行优化,计算了一组优化的偏心块选择。不足之处,首先对土壤本身固有属性,刚度和阻尼的试验有限,对各种压实材料的数据量还有限,这将对优化算法模型准确性大打折扣;其次,当偏心块的数量增多时,其组合关系将会大大增加,这将给后期组合计算求解带来一定难度。
[1]何志勇,杨立新.压路机振动液压回路分析[J].建设机械技术与管理.2006,19(10):26-28.(He Zhi-yong,Yang Lin-xin.Roller vibration hydraulic circuit analysis[J].Construction Machinery Technology and Management.2006,19(10):26-28.)
[2]童飞.从“土壤-机器”系统力学的角度探讨振动压路机的参数设计[D].上海:同济大学,2007(3).(Tong Fei.Vibratory roller parameters design From the“soil- machine system”mechanics perspectives[D].Shanghai Tongji University,2007(3).)
[3]彭福人.YZC12 型振动压路机驾驶室舒适性研究[J].建筑机械,2005(4):24-25.(Peng Hu-ren.YZC12 type vibratory roller bridge comfort research[J].Construction Machinery,2005(4):24-25.)
[4]戴德沛.阻尼技术的工程应用[M].北京:清华大学出版社,1991.(Dai De-pei.Damping technology engineering application[M].Beijing:Tsinghua University Press,1991.)
[5]周昌雄,周传磷.优化振动压路机工作参数[J].筑路机械与施工及机械化,2000,17(3):12-14.(Zhou Chang-xiong,Zhou Chuan-lin.Optimization of vibratory roller working parameters [J].Road Construction Machinery and Construction And Mechanization,2000,17(3):12-14.)
[6]肖仁耀,刘政华.压路机减振系统的改进设计[J].中国科技博览,2008(18):8-10.(Xiao Ren-yao,Liu Zhen-hua.Roller damping system improvement design[J].China's Science and Technology Review,2008(18):8-10.)
[7]万汉驰.复合振动压路机作用原理初探[J].建筑机械,2002(10):31-32.(Wan Han-chi.Complex vibration roller action principle trial[J].Construction Machinery,2002(10):31-32.)
[8]庄表中.振动压路机的原理与减振性能的评估[J].振动与冲击,2005,24(1):23-25.(Zhang Biao-zhong.The principle of vibratory roller and the vibration damping performance evaluation[J].Vibration and Impact,2005,24(1):23-25.)

