小波理论及其在地球化学数据处理中的应用综述

赵云华，李东海，柳炳利，武 飞

(1.成都理工大学管理科学学院，成都 610059;2.内蒙古工业大学管理学院，呼和浩特 010051)

随着不同比例尺地球化学数据大量的积累，相应不同的地球化学数据处理方法应运而生，针对单元素和元素组合地球化学数据，传统的处理方法越来越表现出其局限性，尤其当数据具有非线性特征时，最好使用非线性分析方法，如克里格法、混沌、分形和智能神经网络等方法。目前，一些非线性方法，如人工免疫、卡尔曼滤波、傅里叶变换、小波变换已在地球化学数据降噪处理中应用起来。鉴于此，本文主要研究小波分析在地球化学数据处理中的应用。

1 小波理论、应用及去噪方法的研究现状

小波变换的概念是由法国从事石油信号处理的工程师J.Morlct在1974年首先提出的。国外研究小波的时间较早，80年代就有相关的文章和著作发表，Mallat算法是小波理论突破性的成果。我国对小波的研究起步较晚，1994年形成国内的小波研究高潮。随着小波理论的日益完善，它的应用领域也越来越广泛，尤其在信号和图象处理方面［1-6］已取得很多实用成果。现在，平稳信号处理的理想工具仍然是Fuorier分析，但是在实际应用中的绝大多数信号是非平稳的，而特别适用于非平稳信号的工具就是小波分析。小波的提出先是取得了应用成果(如Morlet在地震数据中的处理等)，再形成理论，最后在各个应用领域全面铺开，因而具有实用价值。当前，小波分析以及广泛应用于一些热点领域。

1.1 地震勘探中的应用

小波在地震勘探中的应用可以概括为:去噪、信号分离、提高地震资料的分辨率、地震数据压缩、有期预测等。地震勘探是地球物理勘探中的发展最快的一项技术，在石油勘探中发挥着突出的作用。由于小波变换同时具有空间域和频率域的局部性，因此它是描述、检测函数奇异性的有效工具，故在地震勘探中取得了大量的成果［7-11］。

1.2 在信号和图像处理中的应用

小波分析已成为信号处理的一种新工具和新方法，且取得了很多成功的应用。如:信号的分解和重构，信号消噪，信号的奇异性检测与分析，模式识别等。小波分析在图像处理中，图像特征提取，图像识别等方面的应用最为成功，另外在图像压缩编码、图像增强、图像去噪、图像融合、图像分解、处理边缘检测等方面［12-15］也广泛应用。

1.3 在物化探数据方面(除地震勘探外)的应用

1999年，陈建国、夏庆霖利用小波对实际物化探异常进行了不同尺度分解，为物化探异常的区域背景及局部异常的提取提供了新的途径［16］;陈玉东在2006年利用旋转反投影法由位场一维连续母小波构造出二维连续母小波，在理论模型上进行了二维连续小波变换，估计了场源的尺度指数，识别出了重力场源的类型，实现了重力场源的快速反演［17］;侯遵泽，杨文采［18-19］利用二维小波多尺度分析方法对中国布格重力异常进行了分解，并从其中划分出有意义的剩余异常，为重力解释和研究地壳的结构提供新的依据;2009年，申维、房丛卉等人［20］在Mandamah地区的物探数据及其铜矿预测中的应用中，利用小波变换后的数据分布曲线图能够识别已知的铜矿化区域，预测未知的矿化区，为电磁法找矿提供了一种有效的方法。总之，小波理论在地球物理勘探中被广泛应用［21-23］，而在化探数据方面也有一定的应用成果［24-28］。

1.4 与其他方法结合的应用

如基于小波变换和数学形态学的边缘检测算法能有效地抑制多种噪声对边缘检测的影响，能较好地保持图像边缘的细节信息，提取的边缘完整连续，对各种不同类型的图像具有很好的鲁棒性［29-33］;在神经网络中，小波理论提供了一个对前传网分析和理论框架［34-37］，小波形式在网络构造中被用来使包含在训练数据中的频谱信息具体化，使用小波变换设计处理网络，可使训练问题大大简化，把小波分析与神经网络结合起来，可对设备进行智能化诊断，小波分析可给出惯性导航系统初始对准的线性和非线性模型;与分形技术［38-42］、混沌理论［43-44］的结合在图像处理、预测中也大量应用。

1.5 小波去噪方法发展与研究

小波去噪方法研究［45-51］自1992年Mallat建立了小波变换快速算法，运用于信号和图像的分解与重构以来，至今20年的时间方法不断涌现并完善。1999年，Mallat提出的利用小波变换模极大值原理进行信号去噪是小波去噪的最经典的方法;XU等人在1994年提出了一种基于空域相关性的噪声去除方法;Pna等人在1998、1999年推导出噪声能量阈值的理论计算公式，并给出了一种估计信号噪声方差的有效方法，使得空域相关滤波算法具有自适应性。Dnohoo和Jhonstnoe等人在1995年提出了信号去噪的软阈值方法和硬阈值方法;Gao和Burce把软阈值和硬阈值方法进行推广，提出了Semisotf阈值方法;Jansen等人1997年采用GCV估计器来估计小波阈值，从而对图像中的相关噪声进行去除。2000年Chnag等人提出一种针对图像的Byaes Shrink阈值去噪方法，取得了很好的去噪效果。近年来，小波阈值去噪方法在算法的可行性改进与创新中不断完善［45-47］。

2 地球化学数据处理中的小波变换

2.1 小波变换基本原理

小波变换是以某些特殊函数为基将数据过程或数据系列变换为级数系列以发现它的类似频谱的特征，从而实现数据处理。

设函数ψ∈L2(R)∩L1(R)，并且(0)=0，由ψ经伸缩和平移得到一族函数

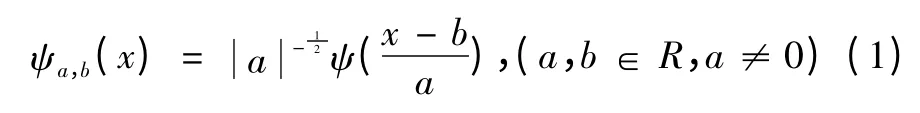
称{ψa，b}为连续小波，称ψ为基本小波或母小波。其中，a为伸缩因子，b为平移因子。

对任意一个信号f∈L2(R)，其连续小波变换定义为

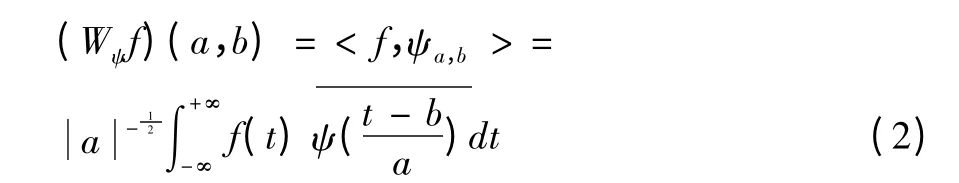
在实际计算机算法中常采取离散小波变换(DWT)算法。我们把式(1)中的参数a，b都取离散值，固定伸缩步长a0＞1，位移步长b0≠0，取a=，b=nb0，从而把连续小波变成离散小波，即

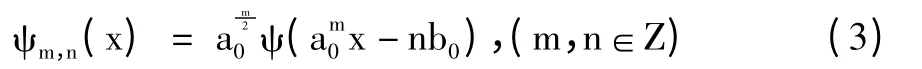
设ψ为基本小波，称式(3)定义的函数族ψm，n(x)m，n∈Z为离散小波，对于信号f∈L2(R)，其离散小波变换定义为

2.“版权专有使用授权书”可在本刊网站的“投稿指南”下载；签名作者的顺序及人数一定要与稿件一致；不方便签字者，可由第一作者或通讯作者代签；加盖单位公章。

将小波系数还原成数据的过程叫小波重构，相应的离散小波重构公式为:

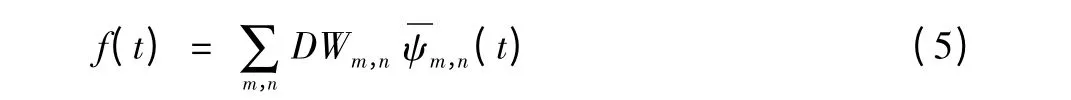
2.2 小波去噪的基本原理及步骤

在小波分析的许多应用中，都可以归结为信号处理问题。信号有三大类小波去噪方法:即基于小波变换模极大值原理的去噪方法，小波阈值去噪方法以及基于小波变换尺度相关性的去噪方法，本文主要研究探讨小波阈值去噪法。

2.2.1 一维信号f(t)小波阈值去噪的基本步骤

(1)分解过程:选择合适的小波基函数和小波分解层数j，对汗噪信号f进行小波分解，得到一组小波系数:d1，d2，…，dj，cj(图1)。

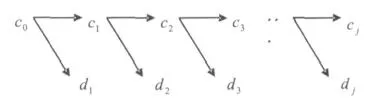
图1 分解过程示意图

(2)阈值作用过程:对分解的高频系数dj进行阈值处理，得到新的小波系数。

(3)重构过程:利用小波逆变换，用小波分解的低频系数cj以及阈值量化处理后的高频系数^dj进行小波重构(图2)。

图2 重构过程示意图

二维信号f(x，y)，一般指图像，其小波阈值去噪的一般步骤为:

(1)分解过程:对实际信号f进行二维小波分解，选择一个小波并确定分解层次N，然后进行分解计算:f=c⊕dH⊕dV⊕dD(图3)。

图3 三级小波变换分解示意图

(2)作用域值过程:对所有的分解信号高频系数dH、dV以及dD进行阈值处理，得到新的信号以及。

事实上，二维离散小波变换是先对信号沿X轴，再沿Y轴(或反之)各做一次一维的小波变换，在每一小波尺度上，信号将被分为近似(低频)信号(c)、水平方向信号(dH)，垂直方向信号(dV)以及对角线方向信号(dD)4个子信号。再对近似子信号应用二维小波变换，构造下一尺度的4个子信号，直到达到目的尺度为止。将信号经二维离散变换后，在频域内据噪声和信号的频谱特性不同，对高频成分加以衰减可除噪。二维小波算法流程如图4所示。

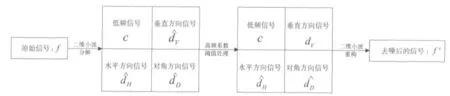
图4 二维小波算法流程图

2.3 小波在地球化学数据处理中的应用思路

地球化学数据中的“噪声”是地球化学数据在经采样、预处理和分析等一系列过程中相应产生的采样误差、预处理误差和分析误差叠加形成的，因此如何有效地消除噪声，提高地球化学数据的准确性和有效性是关键所在。

小波分析作为一种新的时频分析工具，在信号、图像处理方面，理论与实际技术都已成熟，在地球化学中用的较少，但其算法思想符合地球化学数据的空间分布特征。地球化学数据是在连续空间(现实空间)上采样得到的一系列点的集合，我们习惯用一个二维矩阵表示空间上各点，则可由z=f(x，y)来表示，f(x，y)表示为式(6)。由于空间是三维的，地球化学数据表现形式为二维的，因此在空间中另一个维度上的关系就由梯度来表示。

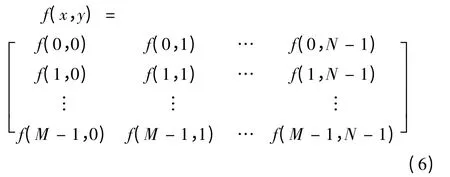
其中，M为行数，N为列数，矩阵的每个元素代表某一元素(如Cu)的含量值。

本文提出利用二维小波变换对地球化学数据进行降噪处理，其处理步骤如图5所示。

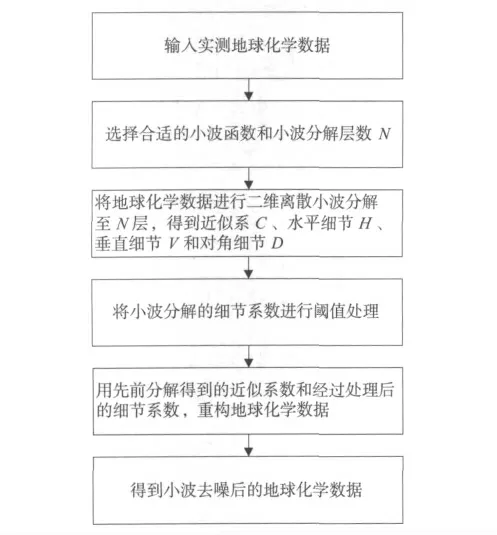
图5 小波去噪处理地球化学数据流程图

3 结束语

总之，小波分析理论日益完善，它的应用领域也越来越广泛，并已取得很多实用成果，但仍然有一些根本性的问题尚待解决。小波并不是“万能”的工具和方法，应用问题是否适合于小波分析，必须视实际问题而定。此外小波理论与分形、神经网络等一些非线性方法已有一定的结合，但在应用的过程中本质上的突破并不多，甚至还出现了一些新的问题有待解决。如何开辟一些小波新的应用研究领域也是一个非常富有挑战性的课题。本文旨在研究小波的最新理论，进一步完善从小波理论到小波应用的桥梁，力求探索小波理论在地学方面的应用。

[1]任传波，郝丽霞.小波变换及其在图像处理中的应用[J].山东工程学院学报，1999，13(2)：16-19.

[2]李继军.小波分析及其在信号、图像降噪中的应用研究[D].西安：西安电子科技大学，2006.

[3]王剑平，张 捷.小波变换在数字图像处理中的应用[J].现代电子技术，2011，34(1)：91-95.

[4]王学玲，闫晓薇.小波变换在信号处理中的应用[J].福建电脑，2006(9)：89-90.

[5]于海珠，郭 辉，管玉玲.小波变换在图像处理中的应用[J].人工智能及识别技术，2011(18)：117-118.

[6]肖大雪.Matlab小波分析在信号处理中的应用[J].科技广场，2011(1)：60-64.

[7]汤谨晖.小波理论在地震数据处理中的应用综述[J].科技广场，2010(6)：150-152.

[8]张旭莲.小波变换及其在地震消噪中的应用[D].西安：西安科技大学-2006.

[9]赵玉宝.小波变换在地震信号消噪中的应用研究[D].长沙：中南大学，2005.

[10]裴正林.小波理论及其在地震数据处理中的应用[J].地球物理学进展，2002，17(3)：486-497.

[11]姚建红.基于小波变换的地震勘探信号处理技术研究[D].大庆：大庆石油学院，2009.

[12]刘 杨.基于小波变换的图像阈值去噪研究与实现[D].成都：成都理工大学，2011.

[13]张永军.小波理论及其在信号处理中的应用[J].空间电子技术，2009(4)：25-30.

[14]朱 磊.多小波图像去噪算法研究应用[D].哈尔滨：哈尔滨工程大学，2006.

[15]储鹏鹏.基于小波变换的图像去噪方法研究[D].西安：西安电子科技大学，2009.

[16]陈建国，夏庆霖.利用小波分析提取深层次物化探异常信息[J].地球科学-中国地质大学学报，1999，24(5)：509-512.

[17]陈玉东.二维连续复小波变换识别重力场源[J].物探与化探，2006，30(2)：141-147.

[18]侯遵泽，杨文采.中国大陆重力场小波分析与油气勘查愿景规划[J].黑龙江大学自然科学报，2011，28(3)：281-284.

[19]杨文采，施志群，侯遵泽，等.离散小波变换与重力异常多重分解[J].地球物理学报，2001，44(4)：534-541.

[20]申 维，房丛卉，常兴国.小波分析在M andamah地区的物探数据及其铜矿预测中的应用[J].物探化探计算技术，2009，31(6)：525-529.

[21]李冀蜀.浅谈小波理论在地球物理勘探中的应用[J].勘探开发，2011(9)：180-181.

[22]向 峰.小波理论在地球物理勘探中的应用[J].内蒙古石油化工，2008(13)：22-23.

[23]段虞荣，郑继明，段绍光.小波分析在油气田地球物理勘探中的应用[J].重庆大学学报：自然科学版，1996，19(6)：44-53.

[24]曹殿华，王安建，王高尚，等.勘查地球化学异常多尺度分析方法-以赣东北德兴矿集区为例[J].现代地质，2008，22(6)：1028-1033.

[25]黄厚辉，郭 科，唐菊兴.基于小波多尺度分析的异常下限确定方法[J].地质找矿论丛，2007，22(4)：311-320.

[26]王晓敏，张晓军，华 杉，等.小波勒山地区1：5万地球化学数据处理与异常评价[J].地质与勘探，2010，46(4)：681-686.

[27]雷 丽，王绪本，倪师军，等.小波分析在化探异常处理中的试验研究-以四川石棉田湾矿区为例[J].矿物岩石，2000，20(3)：91-94.

[28]文战久，刘洪臣.地球物理和地球化学异常的多重分形分析与分解[J].地球物理学进展，2007，22(3)：972-978.

[29]黄海龙，王 宏.一种基于小波变换和数学形态学的边缘检测算法[J].东北大学学报：自然科学版，2011，32(9)：1315-1318.

[30]吕 洁，王金海，郑 羽.基于图像边缘检测的小波去噪算法[J].天津工业大学学报，2007，26(5)：64-67.

[31]唐 敏.基于边缘与角点检测的特征提取方法与应用研究[D].长沙：国防科技大学，2006.

[32]王 博.数字图像处理方法与应用研究[D].西安：西北工业大学，1998.

[33]管聪慧.基于相关性及边缘保持的小波图像降噪方法研究[D].青岛：青岛大学，2007.

[34]赵林明，楚清河.基于小波分析与人工神经网络的水轮机压力脉动信号分析[J].水利学报，2011，42(9)：1075-1080.

[35]刘 辉，田红旗，李燕飞.基于小波分析法与神经网络法的非平稳风速信号短期预测优化算法[J].中南大学学报：自然科学版，2011，42(9)：2704-2711.

[36]李小玉，何怡刚.基于小波分析和遗传神经网络的模拟电路故障诊断方法[J].计算机应用研究，2011，28(12)：4517-4524.

[37]岳耀雪.小波神经网络在手写数字识别中研究与应用[J].电脑编程技巧与维护，2010(14)：85-87，97.

[38]李 娜，初 雪.小波分析在各领域中的应用及展望[J].齐鲁师范学院学报，2011，26(5)：112-116.

[39]曹茂森，任青文，王怀洪.基于小波与分形理论的地震异常检测[J].地球物理学报，2005，48(3)：672-679.

[40]赵 健，潘建寿.小波分形结合在图像处理中的应用研究[J].计算机工程，2005，31(1)：29-31.

[41]陈家琪，唐元刚.小波与分形混合图像压缩编码[J].科技信息，2007(35)：272-274.

[42]王 飞.图像处理中的小波与分形结合应用研究[J].科技视界，2012(28)：268-273.

[43]刘家胜，黄贤武.基于混沌与小波变换的图像加密算法[J].微电子学与计算机，2007，24(12)：6-12.

[44]殷光伟，郑丕谔.基于小波与混沌理论的股市多步预测研究[J].辽宁工学院学报，2005，25(1)：64-67.

[45]扶 晓，陈柳巍.基于小波分析的阈值降噪算法研究[J].电脑编程技巧与维护，2012(4)：90-91.

[46]周祚峰，水鹏郎，李军侠.基于自适应窗的小波域图像去噪算法[J].西安电子科技大学学报，2007，29(8)：1238-1241.

[47]张维强，宋国乡.基于一种新的阈值函数的小波域去噪信号[J].西安电子科技大学学报，2004，31(2)：296-299.

[48]陈明举，杨平先.基于拉普拉斯模型的双树复小波域图像降噪[J].四川理工学院学报：自然科学版，2012，25(3)：55-58.

[49]LiQ M，Cheng Q M.Visual anomaly：a GIS based multifractal method for geochemical and geophysical anomaly separation in Walsh domain[J].computer&geoscience，2006，32(5)：663-672.

[50]LiC J，Ma T H，Shi JF.Application of a fractalmethod relating concentrations and distances for separation of geochemical anomalies from background[J].Journal of Geochemical Exploration，2005，77(2-3)：167-175.

[51]Bos M，Hoogendarm E.Wavelet transform for the evaluation of peak intensities in flow-injection analysis[J].Anal.Chim.Acta.，1992，267(1)：73-80.