几类紧集的box维数

陈飞燕, 李同兴

(南京财经大学 应用数学学院, 江苏 南京 210046)

几类紧集的box维数

陈飞燕, 李同兴

(南京财经大学 应用数学学院, 江苏 南京 210046)

分形几何中非空有界集的box维数是应用最广泛的分形维数之一. 研究了三类紧集的box维数,给出了它们的box维数的计算公式,从而推出了三个常用紧集的box维数值.

有界集; 紧集; 覆盖; Hausdorff维数; box维数

0 引言

维数是空间和集合建立如何度量的关键,如在经典的欧氏空间中,点是0维的,直线是1维的,而平面和立方体的维数分别是2维和3维的.有时我们把维数看作自由度,直线上的点可用一个实数表示,平面上的点可用2个实数表示,一般的n维欧氏空间有n个自由度,其中的点需要用n个实数(x1,x2,…,xn)来表示.Poincare和Lebesgue都曾对维数进行过深入研究,但是总的来说效果不够理想.然而使维数研究取得重要进展的,首先应归功于Hausdorff,他于1919年在测度基础上,引入了适用于任何集合的Hausdorff维数的概念.但是要想计算一个一般集合的Hausdorff维数确实比较困难.因此人们就提出了计算及经验估计相对简单的而且应用最广泛的集合的box维数.下面先回顾一下box维数的概念.

定义设F⊂Rn是一个非空有界集,用N(δ,F)表示直径最大为δ,可以覆盖F的集合的最小个数,则F的下,上box维数分别定义为

1 主要结论及其证明

以下我们研究实数集R中三类常用紧集的box维数的规律性.

证明设U是一个区间,其长度

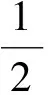
取k是满足

利用洛必达法则[4]知,极限

所以

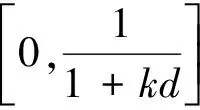
于是可以得到

从而有

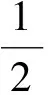
故

所以

另一方面,

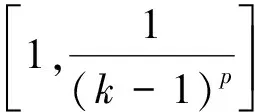
再利用洛必达法则求极限可得,

3 简单实例

通过求解以上三类紧集的box维数,我们发现了它们具有一定的规律性.利用这些结果我们可以给出下列三个常用的特殊紧集的box维数.

[1] Falconer K. Fractal Geometry: Mathematical Foundations and Applications[M]. New York: Wiley, 1990.

[2] 李水根. 分形[M]. 北京: 高等教育出版社, 2004.

[3] 沙震,阮火军. 分形与拟合[M]. 杭州: 浙江大学出版社, 2005.

[4] 华东师范大学数学系. 数学分析[M]. 上册. 3版. 北京: 高等教育出版社,2001.

BoxDimensionsofSeveralCompactSets

CHEN Fei-yan, LI Tong-xing

(School of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing Jiangsu 210046, China)

The box dimension of a nonempty bounded set is one of the most widely used fractal dimensions in the fractal geometry. In this paper, we study and calculate the box dimensions of three kinds of compact sets, and then from which we present the box dimensions of three common compact sets

bounded set; compact set; cover; hausdorff dimension; box dimension

2013-02-13

陈飞燕(1989-), 女, 江苏镇江人, 硕士研究生, 研究方向为非线性分析及其应用.

O175

A

1671-6876(2013)02-0117-03

[责任编辑李春红]