定积分定义在证明和求极限中的应用*

曾 静，程珍珍，耿立刚

(重庆工商大学数学与统计学院，重庆400067)

0 引言

设f(x)是定义在［a，b］上的一个连续函数，I是一定数.若任意给定的ε＞0，存在σ＞0，对任意的分法a=x0＜x1＜ … ＜xn－1＜xn=b，不论点 ξi在小区间［xi－1，xi］中如何选取，只要 λ =max{Δx1，Δx2，…，Δxn}＜ δ，就有＜ ε，则称 I是 f(x)在［a，b］上的定积分［1］，记为

值得注意的是定积分的值只与被积函数和积分区间有关，与区间的划分方法以及点ξi的选取方法无关［2］.正因为这个特性，在划分区间以及选取点ξi时，选取一些特殊而恰当的方式，可以帮助求解一些关于定积分的证明以及一些复杂的求极限问题［3］.

1 定积分定义在证明中的应用

在定积分定义的区间划分方式中，选择等分区间，选取点ξi时，选择小区间的一个端点，可以帮助求解一些关于定积分的证明题.

例 1 求证若 f(x)∈R［0，1］，f(x)≥a ＞0，则

证明 取Pn为区间［0，1］的一个划分，}，它将［0，1］划分成n个等份小区间，故每个小区间的长度都是，区间长度最大值为λ=要使 λ →0，则n →∞.在区间［xi－1，xi］中选取点 ξi=xi，则有

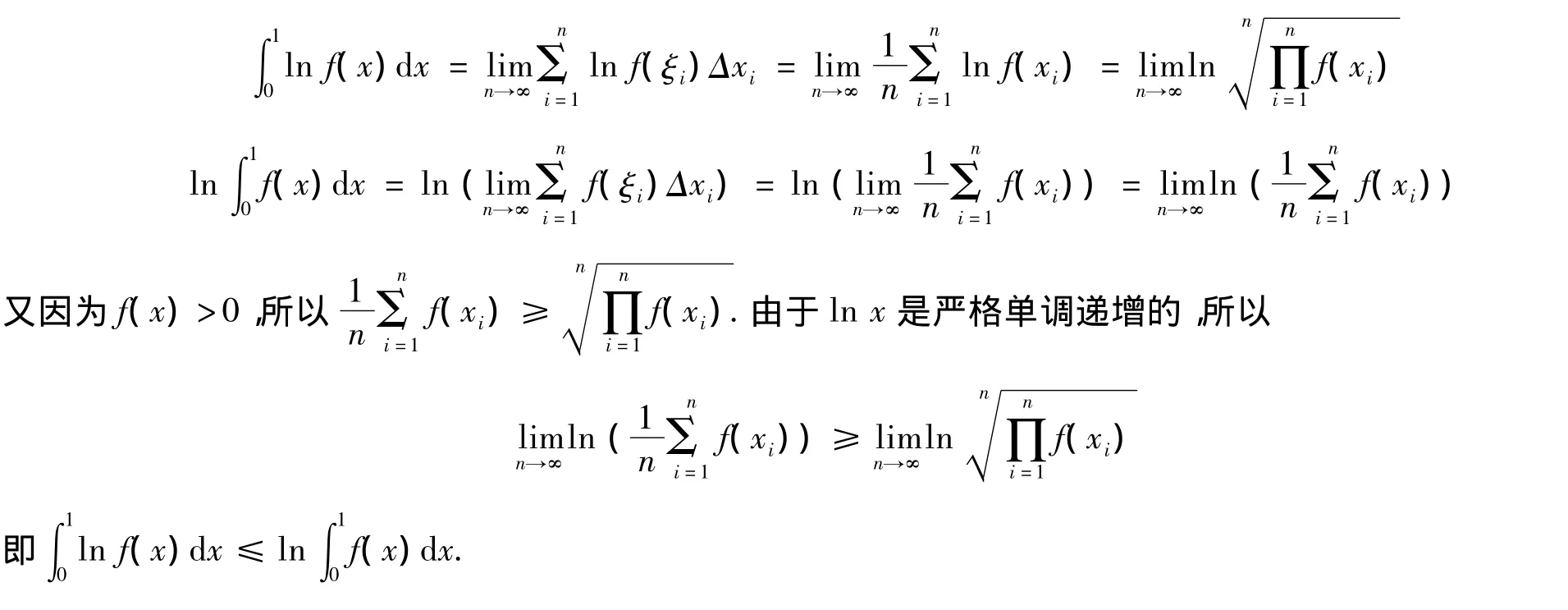
2 定积分定义在求极限中的应用

定积分是通过极限定义的，反过来一些求极限的问题也常常通过定积分来求解.求解过程中，也常常利用定积分定义中区间划分及点ξi选取的任意性这一特性.

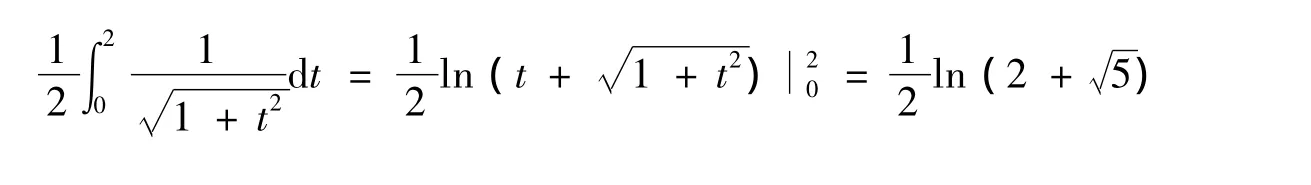
3 小结

在定积分的学习过程中，充分理解和掌握定积分定义中区间的划分方法、以及点ξi的选取方法与定积分值无关这一特性，将有助于证明一些关于定积分的复杂证明题.同时，逆向思考极限与定积分定义之间关系，有利于求解一些复杂的求极限问题.总之，在学习新概念的时候，必须深刻理解新概念的精髓和本质，这样才能做到活学活用.

［1］欧阳光中，朱学炎，金福临，陈传璋.数学分析［M］.3版.北京:高等教育出版社，2007

［2］邓乐斌.数学分析的理论、方法与技巧［M］.武汉:华中科技大学出版社，2005

［3］李焕荣，宋证远.关于复合型数值求积公式的几点注记［J］.重庆工商大学学报:自然科学版，2012，29(3):51-54