铁电材料Pb（Zr1－xTix）O3 的电热效应

封文江，尹小荷，张 思，孟萍萍，朱 影，何江海，王传银

（1.沈阳师范大学 物理科学与技术学院，沈阳 110034；2.沈阳师范大学 实验中心，沈阳 110034）

0 引 言

锆钛酸铅（Pb（Zr1－xTix）O3，PZT）是由Jaffe发现的具有铁电效应的固溶体材料（x＝0.53时压电常数d33为600×1012C／N）［1］。PZT是PbTiO3和PbZrO3的二元连续固溶体，呈钙钛矿结构，x＜0.53时为四方铁电相，0.53＜x＜0.95为三角铁电相。Mischenko等［2］在900kV／cm的高电场下，研究了350nm厚的铁电PbZrO3∶PbTiO3薄膜的电热性质，获得最大温度改变量ΔT＝12K，电热系数为1.4×10－3C／（K·m2）。Kanno等研究了c轴取向的 PbZr0.52Ti0.48O3／MgO 薄膜的热力学特征量［3］。Roytburd等采用极化强度测量，研究了PbZr0.2Ti0.8O3／LaAlO3的内应力［4］。择优取向富锆PZT薄膜的电热效应优于多晶富锆PZT薄膜，且前者的电热温变最大值ΔT＝29K，而后者仅为ΔT＝12K。Fatuzzo和Merz研究认为，电热效应只发生在居里点以上［5］。Mitsui等认为，电热效应只发生在居里温度以下，在该温度以下，材料的自发极化随温度的变化而变化［6］。Jona等认为，电热效应可以产生居里温度以上或者以下，且在居里温度以上的电热效应较大［7］。Thache［8］研究了PZT体系的反铁电陶瓷Pb（Zr0.445Sn0.445Ti0.09）的电热效应，在8kV／cm的电场强度下，体系的最大电热温变为1.1K。Olsen［9］发现 Pb0.99Nb0.02［（Zr0.73Sn0.27）0.93Ti0.07］在2kV／cm 的电场强度下获得电热温变为2K。Tuttle［10］等研究了反铁电陶瓷Pb（Zr0.75Sn0.20Ti0.05）的电热效应，在30kV／cm 电场强度下，该体相材料的电热温变最大值达2.6K。

以前的工作研究了PbTiO3多晶及薄膜材料强电场下的电热效应［11］。在本项工作中，应用基于Landau－Devonshire相变理论和相关参数，研究了（Pb（Zr1－xTix）O3当x＝0.5、0.6、0.7、0.8、0.9时的电热效应，得到极化强度与温度、电场强度的关系曲线，电熵、熵变、比热容与温度的关系曲线。外加强电场使PZT一级相变转变为二级相变，且相变温度逐渐升高。随着Ti含量的增加，熵变的最大值在逐步增加。

1 理论模型与计算参数

对于PZT，利用Landau－Devonshire理论，考虑单畴无约束的自由能密度为

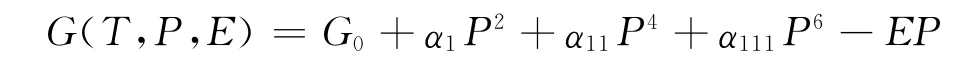
其中：G0（T）为顺电态的能量；T为温度；P为极化强度；E为电场强度；a1、a11、a111为铁电材料的刚性系数。系数a：

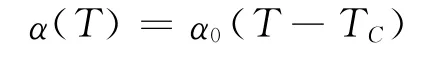
其中，TC为居里温度。由于为居里常数，ε0为真空介电常数。

当E＝0时，从热力学平条衡条件得铁电相变过程中自发极化强度为

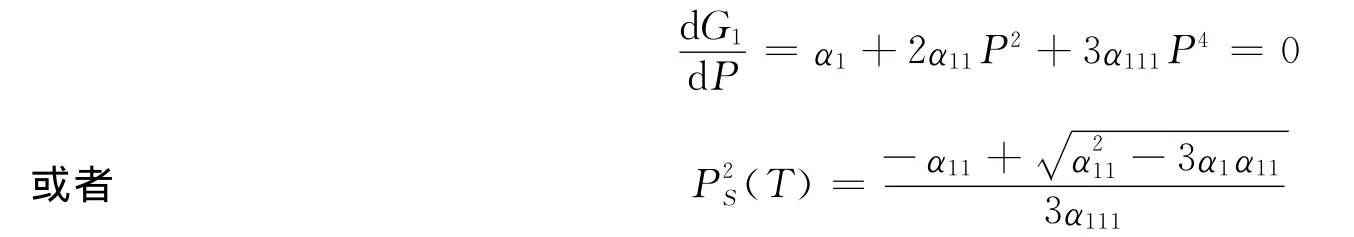
理论计算用到的PZT的各种参数见表1。

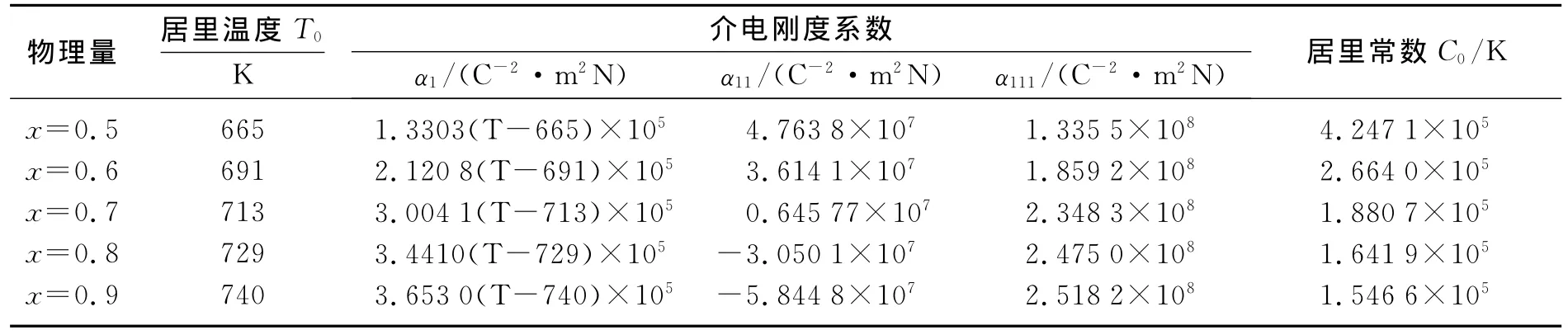
表1 PZT的居里温度、居里常数及介电刚度系数［12－15］

2 结果与讨论

图1a～图1e分别是PZT体材料当x＝0.5、0.6、0.7、0.8、0.9时的极化强度与温度、电场强度的关系曲线。对应的电场强度为0、10、50、100、150MV／m。可以看出，当外加电场为零时，在TC＝665、691、713、729、740K时随着温度的升高发生从铁电到顺电的一级结构相变。可见，随着Ti的增加，居里温度逐渐增大，且一级结构相变也逐渐变为连续的二级相变。这与Mischenko等人的研究结果一致［2］。图1插图为x＝0.5、0.6、0.7、0.8、0.9时T＝515、540、563、580、590K下极化强度与电场的关系曲线。由图可知，PZT（x＝0.5）在515K时矫顽场为2.5MV m－1，PZT（x＝0.6）540K时矫顽场为9.0MVm－1，PZT（x＝0.7）563K矫顽场为22MVm－1，PZT（x＝0.8）在580K时矫顽场为33MVm－1，PZT（x＝0.9）590K矫顽场为41MVm－1。一般来说，只有当外加电场高于矫顽场时，电滞行为才能被消除，相变行为才是可逆的。

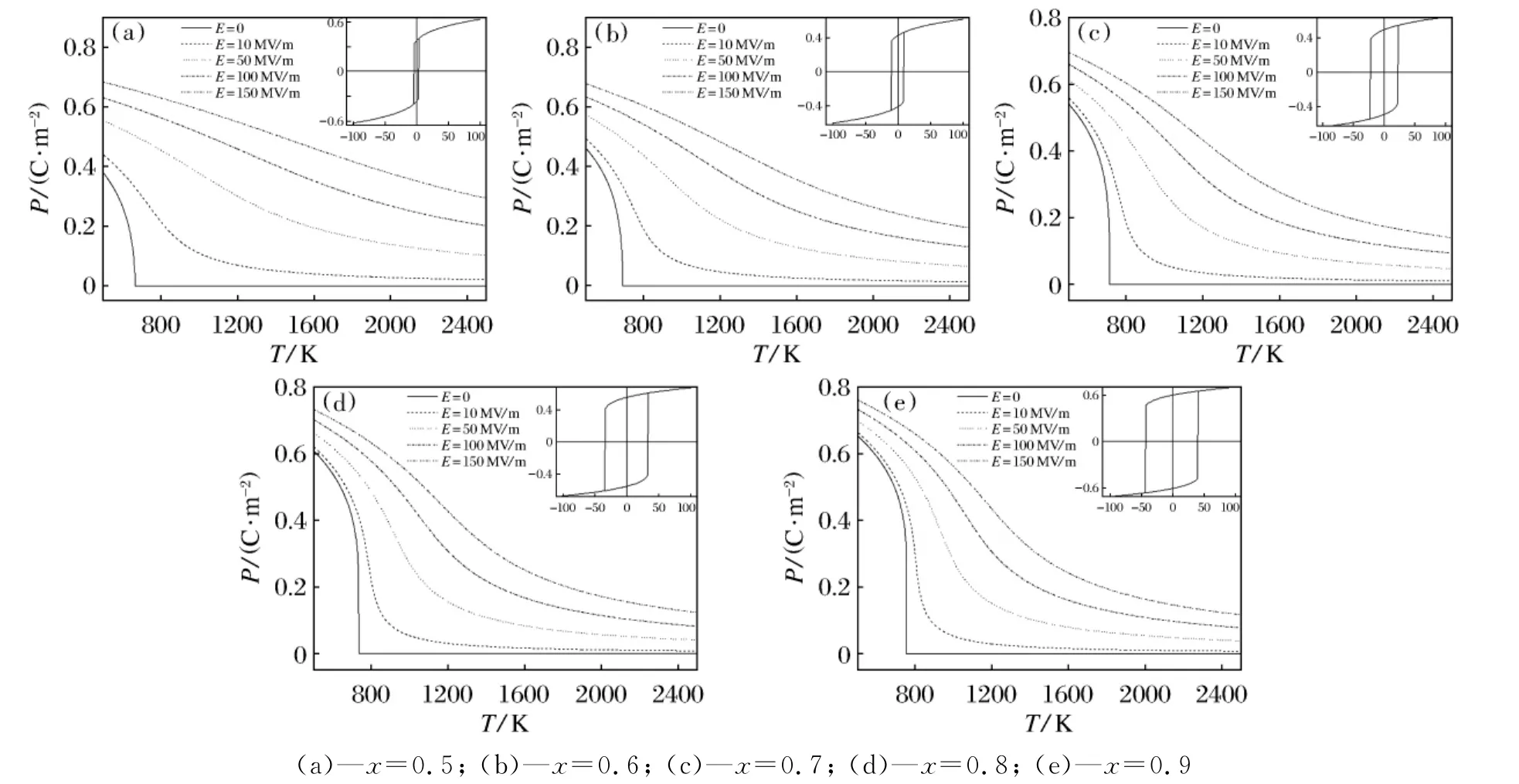
图1 PZT（x＝0.5，0.6，0.7，0.8，0.9）的极化强度和温度关系曲线

图2a～图2e分别为不同电场下PZT（x＝0.5，0.6，0.7，0.8，0.9）电熵与温度的关系曲线。此时电场强度分别为0、10、50、100、150MV／m。显然，不断增强的电场破坏了一级铁电↔顺电结构相变。如图1与图2所示，10MV／m的电场足以使其变为二级相变。当电场为零时，x＝0.5、0.6、0.7、0.8、0.9PZT在T0＝665、691、713、729、740K发生铁电到顺电的结构相变。

图2 不同的电场强度下PZT（x＝0.5，0.6，0.7，0.8，0.9）的电熵与温度的关系曲线

图3a～图3e是x＝0.5、0.6、0.7、0.8、0.9时PZT的等温熵变与温度的关系曲线。随着电场强度强度的增强，熵变逐渐增大。PZT的最大熵变分别为28（对应温度849K）、42（对应温度733K）、60.1（对应温度685K）、75.6（对应温度687K）、87.5（对应温度698K）kJ·m－3K－1。可以看出，随着Ti含量的增加，熵变的最大值在逐步增加。由此可见，富锆PZT块体的最大电热温变出现材料的居里点以上，即当材料由铁电相向顺电相转变之上的200K具有最大的电热效应。

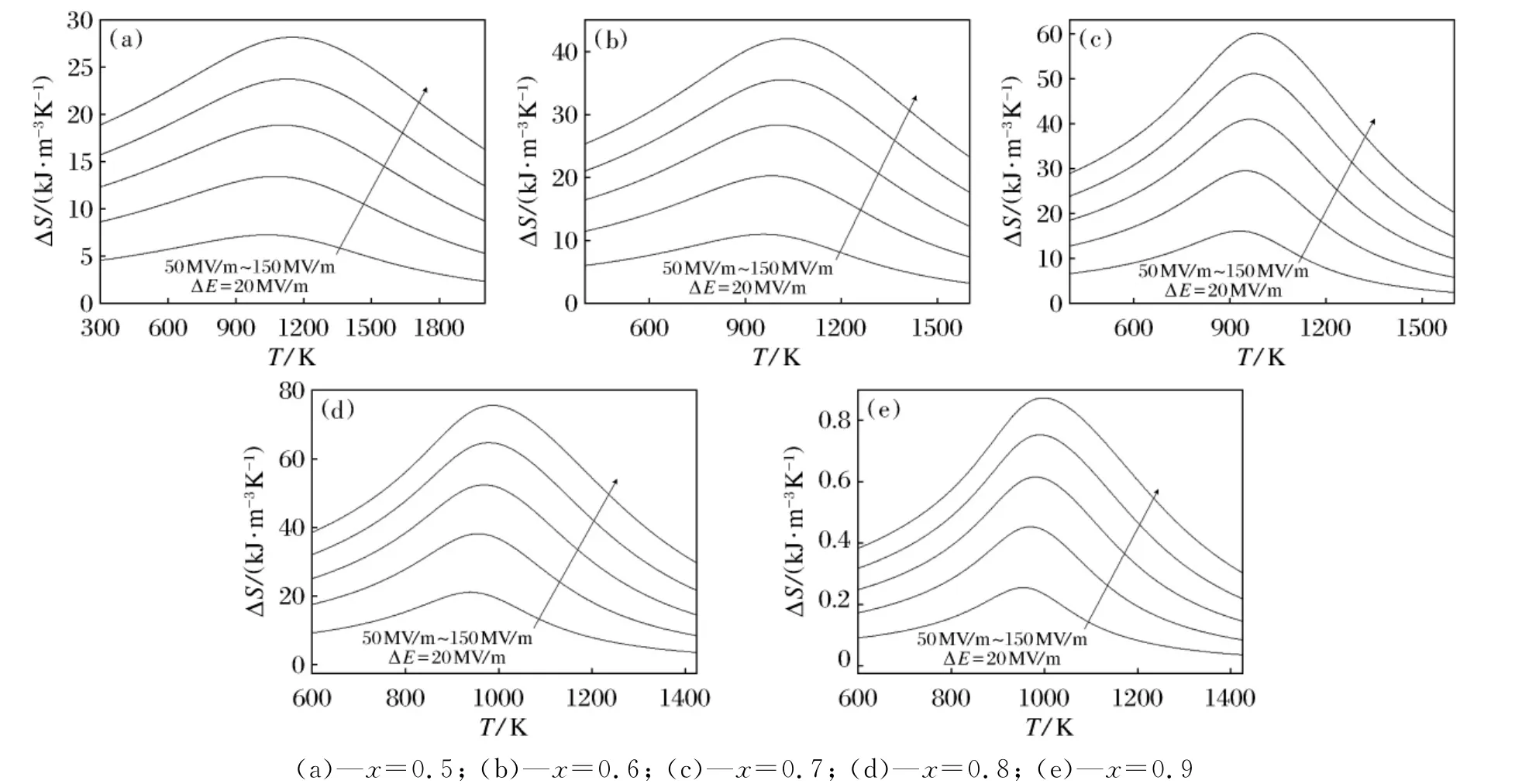
图3 不同的电场强度下PZT（x＝0.5，0.6，0.7，0.8，0.9）的电熵变与温度的关系曲线

图4a～图4e是x＝0.5、0.6、0.7、0.8、0.9时PZT块在电场强度50～150MV／m，DE＝20MV／m的比热容与温度的关系曲线。由图1与2可知，在强电场下一级铁电相变变为二级相变，这就导致了比热容的改变量减小，与电极化强度变化一致（见图1a～图1e）。并且，随着电场强度的增强，相变温度变高。

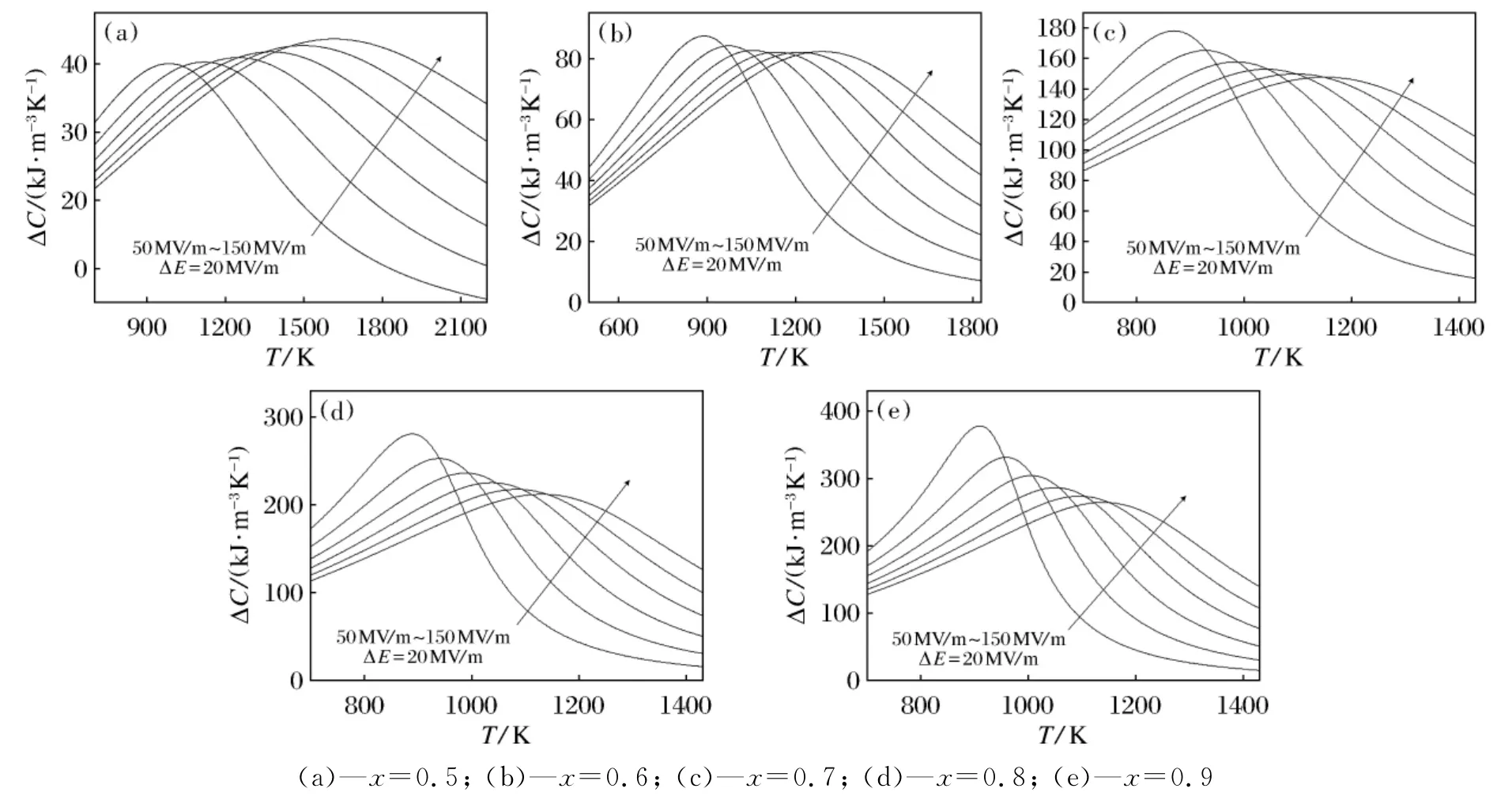
图4 不同电场强度下PZT（x＝0.5，0.6，0.7，0.8，0.9）的比热容与温度的关系曲线

3 结 论

通过Landau－Devonshire的热动力学模型，计算了当x＝0.5、0.6、0.7、0.8、0.9，PbZr1－xTixO3在铁电相变附件的电热效应。结果显示，PZT（x＝0.5，0.6，0.7，0.8，0.9）的居里温度分别为665、691、713、729、740K。并且出现了一级铁电↔顺电转变。强的电场使得PZT块体材料的一级相变逐渐转变为二级连续相变，且相变在更高的温度发生。随着电场的增强，PZT比热容减小，最大电熵变值增强。Ti含量的增加导致电熵变的最大值增大。由此可见，富锆PZT的最大电热温变出现居里温度以上，即居里温度以上200K左右具有最大的电热效应。

［1］JAFFE B，COOK W R，JAFFE H.Piezoelectric Ceramics［M］.London：Academic Press，1971.

［2］MISCHENKO A S，ZHANG Qi，SCOTT J F，et al.Giant electrocaloric effect in thin－film PbZr0.95Ti0.05O3［J］.Science，2006，311（3）：1270－1271.

［3］KANNO I，YOKOYAMA Y，KOTERA H，et al.Thermodynamic study ofc－axis－oriented epitaxial Pb（Zr，Ti）O3thin films［J］.Phys Rev B，2004，69（6）：064103.

［4］ROYTBURD A L，ALPAY S P，NAGARAJAN V，et al.Measurement of Internal Stresses via the Polarization in Epitaxial Ferroelectric Films［J］.Phys Rev Lett，2000，85（1）：190－193.

［5］FATUZZO E，MERZ W J.Ferroelectricity［M］.Amsterdam：North－Holland，1967.

［6］MITSUI T，TATSUZAKI I，NAKAMURA E.Introduction to the Physics of Ferroelectricity ［M］.London：Gordon and Breach，1976.

［7］JONA F，SHIRANE G.Ferroelectric Crystals［M］.New York：McMillan，1962.

［8］THACHER P D.Electrocaloric effect in some ferroelectric and antiferroelectric Pb（Zr，Ti）O3compounds［J］.Appl Phys Lett，1967，39（4）：1996－2002.

［9］OLSEN R B，BUTLER W F.Observation of a polarcaloric（Electrocaloric）in lead zirconate modified with Sn4＋and Ti4＋［J］.Phys Rev Lett，45（17）：1436－1438.

［10］TUTTLE B A，PAYNE D A.The effect of microstrcture on the electrocaloric properties of Pb（Zr，Sn，Ti）O3ceramics［J］.Ferroelectrics，1981，37（1）：603－606.

［11］陈迎杰，封文江，郝爽.PbTiO3多晶及薄膜材料强电场下的电热效应研究［J］.沈阳师范大学学报：自然科学版，2011，29（2）：189－193.

［12］HAUN M J，FURMAN E，JANG S J，et al.Thermodynamic theory of PbTiO3［J］.J Appl Phys，1987，62：3331－3338.

［13］HAUN M J，FURMAN E，JANG S J，et al.Thermodynamic theory of the lead zirconate－titanate solid－solution system：1.Phenomenology［J］.Ferroelectrics，1989，99（1）：13－25.

［14］HAUN M J，FURMAN E，MCKINSTRY H A，et al.Thermodynamic theory of the lead zirconate－titanate solidsolution system：2.Tricritical behavior［J］.Ferroelectrics，1989，99（1）：27－44.

［15］HAUN M J，ZHUANG Z Q，FURMAN E，et al.Thermodynamic theory of the lead zirconate－titanate solidsolution system：3.Curie constant and 6th－order polarization interaction dielectric stiffness coefficients［J］.Ferroelectrics，1989，99（1）：45－54.