约束向量优化问题的像空间分析

罗 彬，王莲明，张 谋

（1.重庆大学 数学与统计学院，重庆401331；2.大连理工大学 数学科学学院，辽宁 大连116024）

在像空间分析（ISA）中，约束向量优化问题的最优性条件可表示为一个参数系统的不可行性，或可等价地表示为约束向量优化问题像空间（IS）中两个适当子集的分离.Chinaie等［1－2］用该方法研究了多值函数及最优解中多值函数的标量化问题；李军等［3］用该方法研究了锥约束变分不等式问题并运用到交通平衡问题中；Mastroeni用该方法研究了约束优化的对偶问题［4］、向量拟平衡问题的鞍点和间隙函数［5］、锥序下的向量拟平衡问题［6］以及向量优化问题的锥分离［7］，并用该方法讨论了向量优化问题的一些最优性条件［8－9］；文献［10］用非线性标量化函数Δ分析非光滑优化问题的几何形状，并获得了非凸优化问题的必要最优性条件.目前，该非线性标量化函数已被应用于各种优化问题［11－16］中.

本文使用非线性标量化函数Δ构造一个非线性弱分离函数和一个非线性正则弱分离函数，通过这些非线性分离函数得到约束向量优化问题的一些充分和必要的最优性条件.

1 预备知识

设Y，Z是两个赋范空间，子集M⊆Y，分别用cl M，Mc，ri M，int M和∂M表示M 的闭包、补集、相对代数内部、拓扑内部和边界.令C是Y中的一个闭凸尖锥，则C的对偶锥为

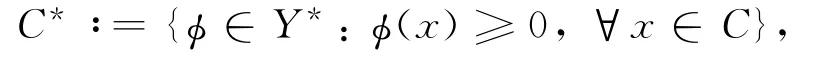
其中Y＊是Y的对偶空间.

设S是一个度量空间，f是定义在S上的函数，α∈ℝ，集合lev≥αf∶＝ ｛x∈S：f（x）≥α｝和lev＞αf∶＝｛x∈S：f（x）＞α｝分别称为f的非负水平集和正水平集.

考虑如下约束向量优化问题：

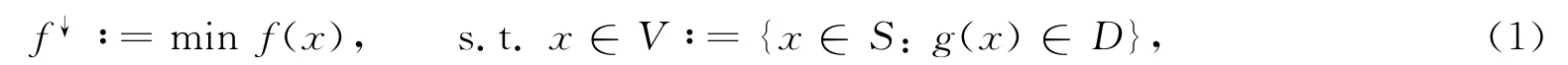
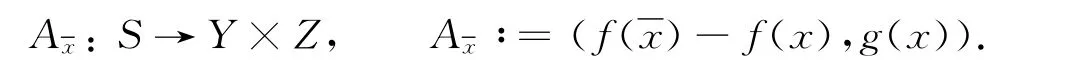
定义集合：

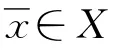
无解，即Kx∩H＝Ø.

定义1 若函数w：Y×Z×Π→ℝ（其中Π是一个参数系统）满足下列两个条件：

则w称为弱分离函数.

由所有弱分离函数组成的集合记为W（Π）.

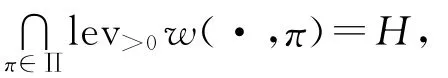
定义3 设Y是一个赋范空间，A是Y的一个子集，定义ΔA：Y→ℝ∪｛±∞｝为

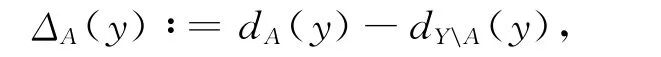
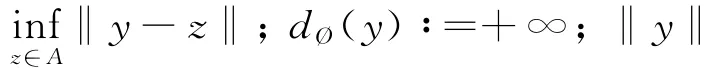
命题1［15］设A是Y的一个非空真子集，则有：

1）ΔA是实值的；

2）ΔA是1－Lipschizian的；

3）当y∈∂A时，ΔA（y）＝0；

4）当y∈int A时，ΔA（y）＜0；

5）当y∈int Ac时，ΔA（y）＞0；

6）当A是一个锥时，ΔA是正齐次的.

2 分离函数

考虑如下非线性分离函数：

命题2 1）当（φ，λ）∈Π1＝H＊＼｛0X×Y｝时，非线性函数w1是一个弱分离函数；2）当（φ，λ）∈Π2＝int C＊×D＊时，非线性函数w1是一个正则弱分离函数.

证明：1）对任意的（φ，λ）∈Π1和（u，v）∈H，有φ（u）≥0和〈λ，v〉≥0.由命题1中3）和4），有

从而有

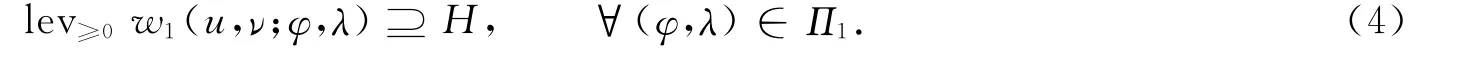
下证

若式（5）不成立，则存在（u，v）∉H 满足

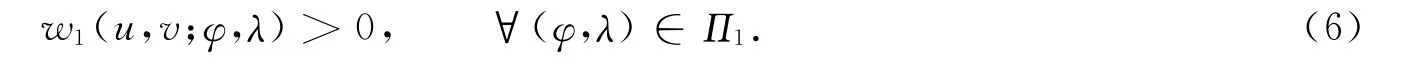
对于（u，v）∉H，分两种情形讨论：

情形1）若u∉C＼｛0Y｝且v∈Z，则存在φ∈C＊，使得φ（u）≤0.令λ＝0Z，则有（φ，λ）∈Π1，但w1（u，v；φ，λ）＝φ（u）≤0，与式（6）矛盾.

情形2）若u∈Y且v∉D，则存在λ∈D＊＼｛0Z｝，使得〈λ，v〉＜0.令φ＝0Y，则由命题1中5）得

与式（6）矛盾.

由式（4），（5）知w1∈W（Π1）.

2）由（φ，λ）∈Π2＝int C＊×D＊，与1）证明同理，有

下证

若式（8）不成立，则存在（u，v）∉H 满足

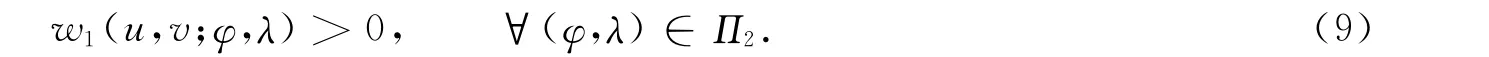
对于（u，v）∉H，分两种情形讨论：

情形1）若u∉C＼｛0Y｝且v∈Z，则存在φ∈C＊，使得φ（u）≤0.令λ＝0Z，则有（φ，λ）∈Π1，而w1（u，v；φ，λ）＝φ（u）≤0，与式（9）矛盾.

情形2）若u∈Y 且v∉D，则存在λ∈D＊＼｛0Z｝，使得〈λ，v〉＜0.显然当t＞0时，有tλ∈D＊＼｛0Z｝，由命题1中5）和6），得

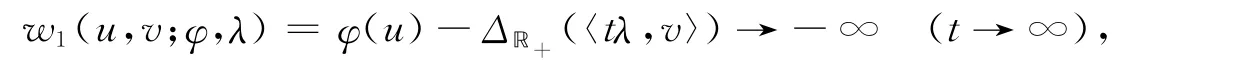
与式（9）矛盾.

由式（7），（8）知w1∈Wℝ（Π2）.

3 最优性条件

先建立择一性定理，然后讨论问题（1）的优化条件.由文献［3］中弱择一性定理和强择一性定理类似可得：

定理1 系统（2）和系统：

不可能同时成立.

由文献［3］中定理4.4.2类似可得：

定理2 系统（2）和系统：

不可能同时成立.

由定理1和定理2可得问题（1）解的一些充分条件和必要条件.

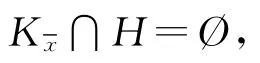
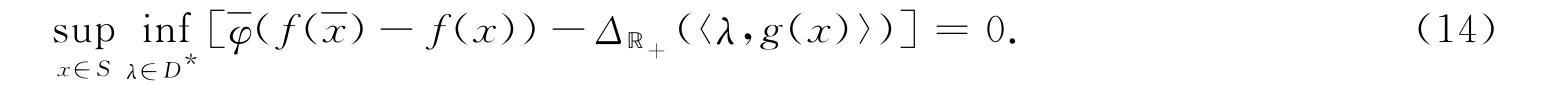
证明：必要性.先证明

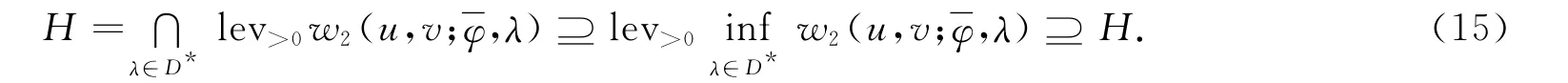
因为w2是一个正则弱分离函数，所以式（15）的第一个等式成立.显然式（15）的第二个等式也成立.下证

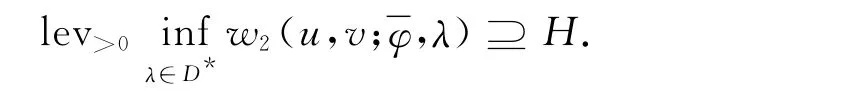
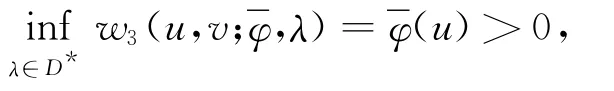
充分性.若式（14）成立，则

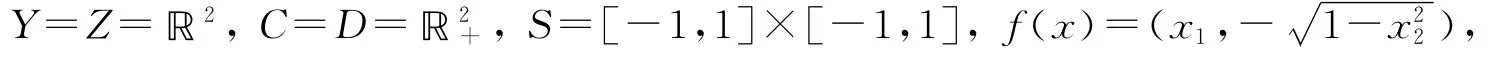
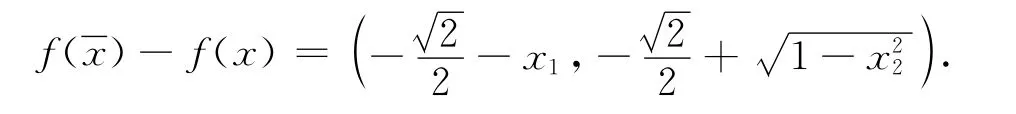
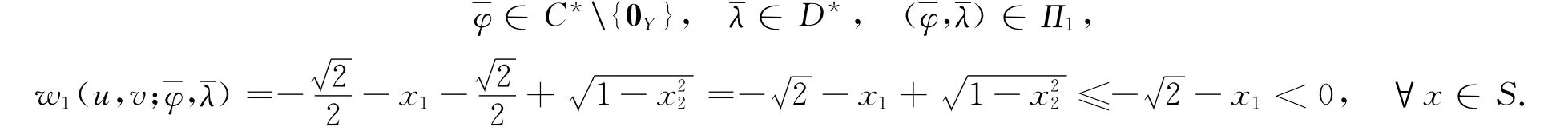
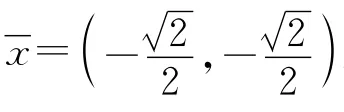
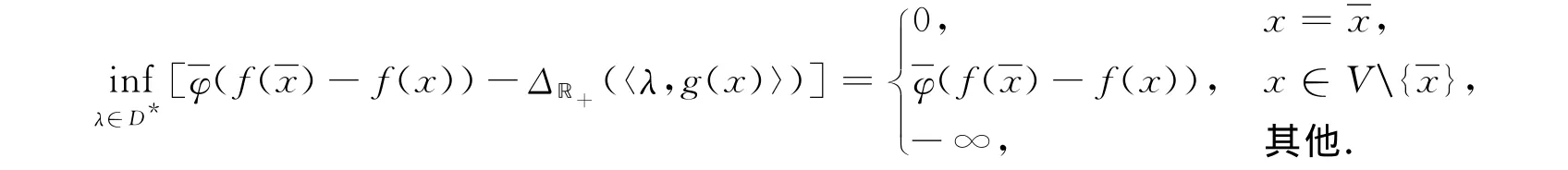
令x∈V，得

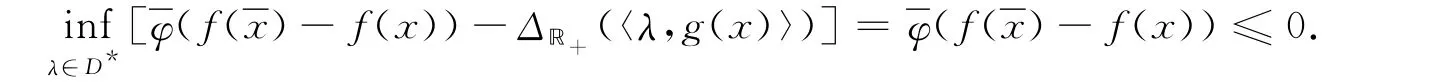
［1］Chinaie M，Zafarani J.Image Space Analysis and Scalarization of Multivalued Optimization ［J］.Journal of Optimization Theory and Applications，2009，142（3）：451－467.

［2］Chinaie M，Zafarani J.Image Space Analysis and Scalarization forε－Optimization of Multifuctions［J］.Journal of Optimization Theory and Applications，2013，157（3）：685－695.

［3］LI Jun，HUANG Nan－jing.Image Space Analysis for Variational Inequalities with Cone Constraints and Applications to Traffic Equilibria［J］.Science China：Mathematics，2012，55（4）：851－868.

［4］Mastroeni G.Some Applications of the Image Space Analysis to the Duality Theory for Constrained Extremum Problems［J］.Journal of Global Optimization，2010，46（4）：603－614.

［5］Mastroeni G.A Separation Approach to Vector Quasi－equilibrium Problems：Saddle Point and Gap Function［J］.Taiwanese Journal of Mathematics，2009，13（2B）：657－673.

［6］Mastroeni G.On the Image Space Analysis for Vector Quasi－equilibrium Problems with a Variable Ordering Relation［J］.Journal of Global Optimization，2012，53（2）：203－214.

［7］Mastroeni G，Pellegrini L.Conic Separation for Vector Optimization Problems［J］.Optimization，2011，60（1／2）：129－142.

［8］Mastroeni G.Optimality Conditions and Image Space Analysis for Vector Optimization Problems［M］.Berlin：Springer－Verlag，2012：169－220.

［9］KOU Xi－peng，PENG Xing－yuan，ZHU Sheng－kun.Second Order Optimality Conditions for Constrained Set－Valued Optimization Problems［J］.Journal of Jilin University：Science Edition，2012，50（2）：244－250.（寇喜鹏，彭兴媛，朱胜坤.约束集值优化问题的二阶最优性条件 ［J］.吉林大学学报：理学版，2012，50（2）：244－250.）

［10］Hiriart－Urruty J B.Tangent Cone，Generalized Gradients and Mathematical Programming in Bananch Spaces［J］.Mathematics of Operation Research，1979，4（1）：79－97.

［11］Li S J，Xu Y D，Zhu S K.Nonlinear Separation Approach to Constrained Extremum Problems［J］.Journal of Optimization Theory and Applications，2012，154（3）：842－856.

［12］Miglierina E.Characterization of Solutions of Multiobjective Optimization Problems［J］.Rendiconti del Circolo Matematico di Palermo，2001，50（1）：153－164.

［13］Zaffaroni A.Degrees of Efficiency and Degrees of Minimality［J］.SIAM Journal on Control and Optimization，2003，42（3）：1071－1086.

［14］Clarke F H.Optimization and Nonsmooth Analysis［M］.New York：Wiley，1983.

［15］Miglierina E，Molho E.Scalarization and Stability in Vector Optimization［J］.Journal of Optimization Theory and Applications，2002，114（3）：657－670.

［16］Amahrop T，Taa A.On Lagrange Kuhn－Tucker Mulitipliers for Muliobjective Optimization Problems ［J］.Optimizations，1997，41（2）：159－172.