变积分限Cauchy核与卷积核混合的完全奇异积分方程的求解

冯 志 新

（吉林师范大学 数学学院，吉林 四平136000）

0 引言与预备知识

Duduchava［1］首次提出了求解如下具有卷积核的积分方程中未知函数φ（t）∈Lp（－∞，＋∞）（0＜t＜＋∞）的问题：

其中：dj∈ℝ；g（t），k0（t）∈Lp（－∞，＋∞）.路见可［2］给出了带有常系数的卷积核与 Cauchy核混合的奇异积分方程，通过由Fourier变换将其转化为Riemann边值问题求解的方法，并在函数类｛0｝中讨论了该方程在正则化情况下的一般解法.文献［3－13］进一步研究了关于卷积核的奇异积分方程的求解问题.本文在上述研究的基础上，考虑含卷积核与奇异核混合的变积分限的完全奇异积分方程的求解问题，先将所研究的积分方程正则化为等价的Fredholm方程，并给出了该类方程可解需添加的条件，再通过求解等价方程得到其在｛0｝类中一般解的数学表达式.

记函数类

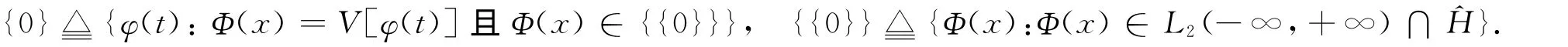
其中Φ（x）＝V［φ（t）］，Φ（x）∈｛｛0｝｝.

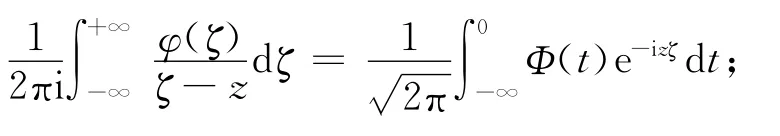
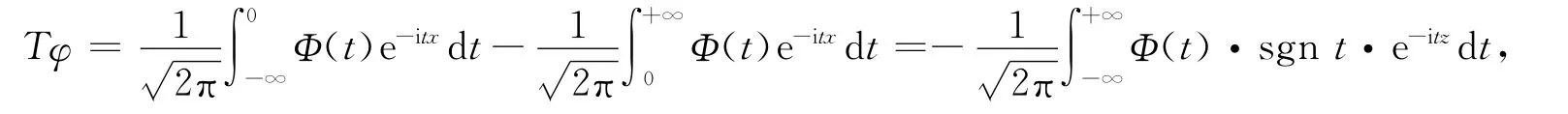
所以Tφ＝－V－1［Φ（t）sgn t］，即V［Tφ］＝－sgn x·Φ（x）.

1 变积分限卷积核完全奇异积分方程的转化

考虑积分方程：

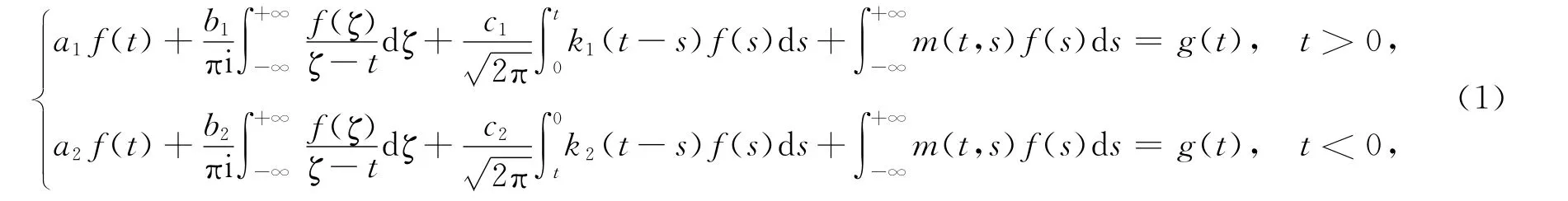
其中：aj，bj，cj为已知常数，且bj≠0，j＝1，2；kj（t），g（t）（j＝1，2）∈｛0｝为已知函数.已知函数m（t，s）∈｛0｝×｛0｝为已知Fredholm核，要求未知函数f（t）∈｛0｝.

方程（1）为变积分限Cauchy核与卷积核混合的完全奇异积分方程，要将其转化为函数类｛｛0｝｝中的完全奇异积分方程，可令

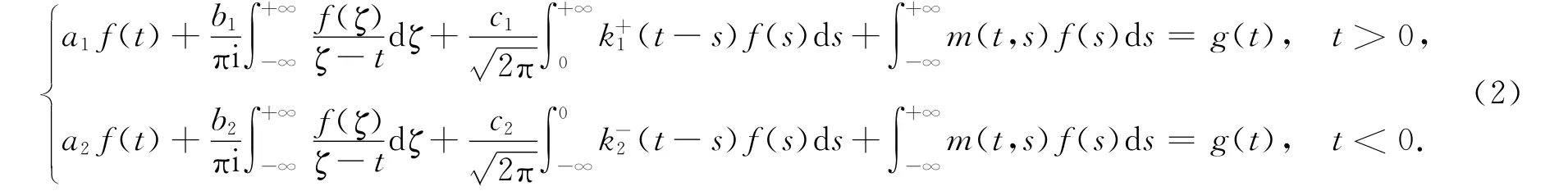
再由f±（t）定义，将式（2）改写为

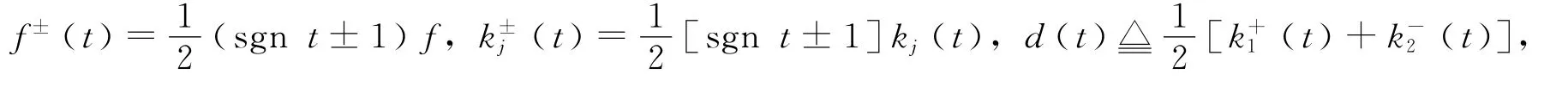
对式（4）两端做Fourier变换V，由引理1，可得

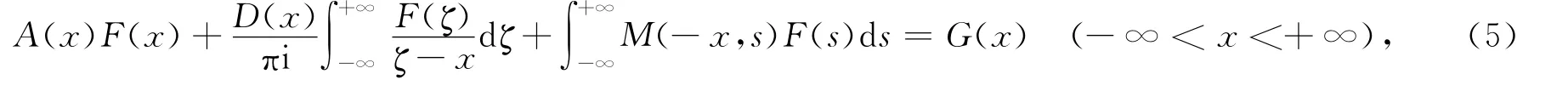
其中：

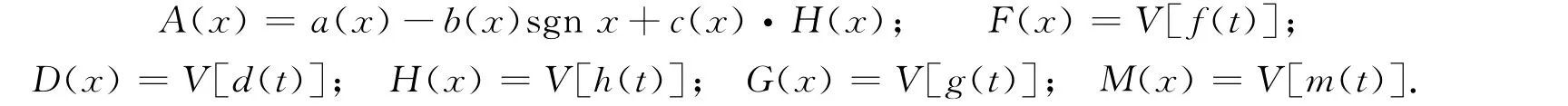
易见，式（5）是在函数类｛｛0｝｝中关于F（x）的完全奇异积分方程.因而，在函数类｛0｝中求解积分方程（1），可转化为在函数类｛｛0｝｝中求解完全奇异积分方程（5）.

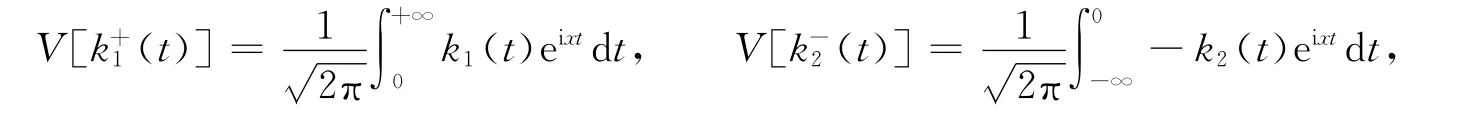
故

假设在x＝0处有A（＋0）＝A（－0），则

若c1≠c2，则

因而，只要式（6）不成立，则A（＋0）≠A（－0），故x＝0是A（x）的第一类间断点.不失一般性，假设上述特殊情况不成立.于是，方程（5）是以x＝0为节点的完全奇异积分方程.

2 积分方程（1）的一般解及可解条件

假设A（x）±D（x）≠0（－∞＜x＜＋∞），即

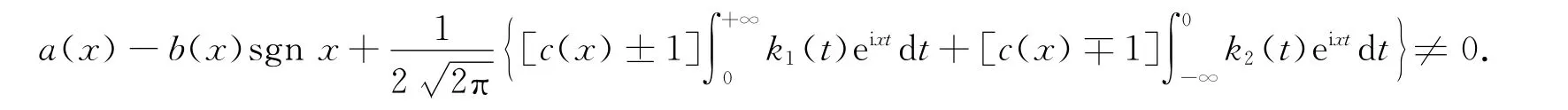
考虑奇异积分方程（5）的特征方程：

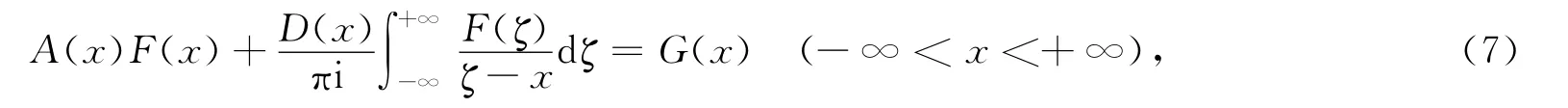
记Φ（z）＝T［F（t）］，由Plemelj公式，方程（7）可写成以x＝0为节点的Riemann问题：

由于本文在函数类｛｛0｝｝中求解Riemann边值问题（8），因此Φ（∞）＝0，于是∞点为问题（8）的特异节点.暂不考虑问题在x＝0处的性质.无穷直线上Riemann边值问题（8）的指标κ按式κ＝－λ∞确定，并按如下方法选取待定整数λ∞：

1）若∞是特异节点，则选取整数α∞，使得λ∞＋α∞＝0；

2）若∞是普通节点且F（z）要求在∞处有界，则选取整数λ∞满足0＜λ∞＋α∞＜1；

3）若∞是普通节点且F（z）要求在∞处允许具有不足一阶的奇异性，则选取的整数λ∞满足－1＜λ∞＋α∞＜0.

根据Cauchy型积分的定义与性质，Riemann边值问题（8）的指标κ＝－λ∞，即κ＝α∞.

当κ≥0时，Riemann边值问题（8）在类R－1中的一般解为

其中：Qκ（z）为κ阶的任意多项式（当κ≤0时，Qκ（z）＝0）；

当κ＜0时，Qκ（z）＝0，则Riemann边值问题（8）在类R－1中的一般解为

由于此时z＝－i是奇异点，为消去在z＝－i处的奇异性，再添加相应的可解条件为

最后，由Φ＋（x）－Φ－（x）＝F（x）及Plemelj公式，可得

其中：

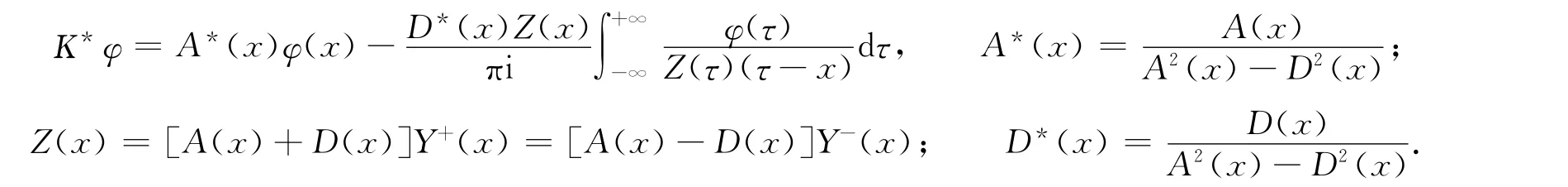
式（12）即为特征方程（7）的一般解（当κ＜0时，Qκ（z）＝0）.

下面对完全奇异积分方程（5）正则化，将式（5）改写成：

当κ≥0时，式（14）的解为

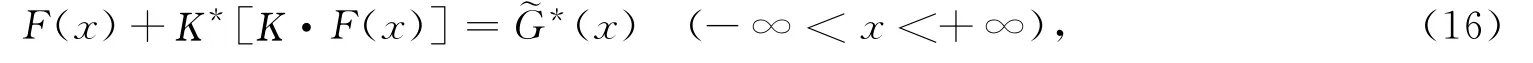
其中：

易证，式（16）即为函数类｛｛0｝｝中的Fredholm积分方程.

当κ＜0时，需添加可解条件，即当

成立时，方程才可解.

因此，在暂不考虑节点x＝0处性态的条件下，求解完全奇异积分方程（5）可转化为：当κ≥0时，与在函数类｛｛0｝｝中求解Fredholm积分方程（16）等价；当κ＜0时，与在函数类｛｛0｝｝中求解Fredholm积分方程（16）（此时Qκ（z）＝0）且满足适当的可解条件等价.

对于Fredholm积分方程（16）（当κ＜0时，Qκ（z）＝0），由Fredholm积分定理及广义预解核理论［10］，可知：

1）当κ≥0时，Fredholm积分方程（16）可解的充分必要条件为

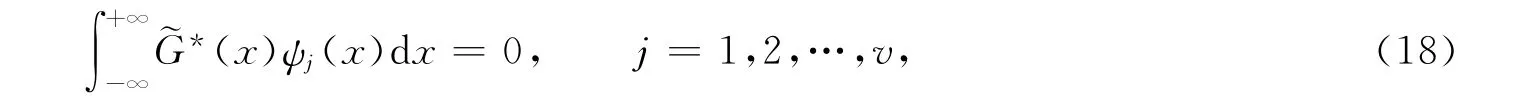
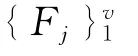
2）当κ＜0且式（17）成立时，Fredholm积分方程（16）（此时Qκ（z）＝0）可解的充分必要条件为

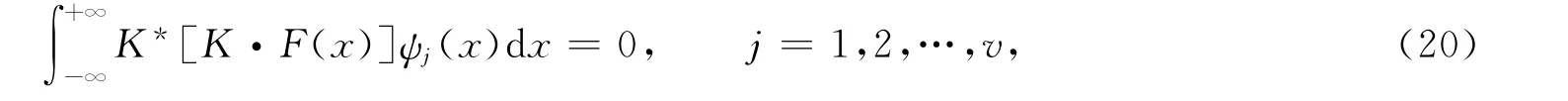
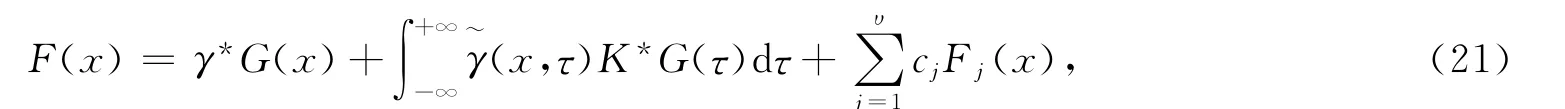
其中γ（x，τ）为方程的广义预解核.因此，方程（1）的解由

给出.

3 积分方程（1）在x＝0处的性态

上述讨论都是假设暂不考虑F（x）或Φ（x）在x＝0处性态条件下进行的，下面考虑为保证F（x）或Φ（x）在x＝0处属于函数类｛｛0｝｝所需的相应条件.

由于x＝0是Riemann边值问题（8）的节点，则其也为变积分限的卷积核与Cauchy核混合的积分方程（1）的节点.由于要求未知函数F（x）∈｛｛0｝｝，在x＝0处必须有F＋（＋0）＝F＋（－0），从而Φ＋（＋0）＝Φ＋（－0）.易见，x＝0是 Riemann边值问题（8）的节点.假设x＝0是 Riemann边值问题（8）的普通节点.当s从x＝0沿实轴右侧趋于0时，记x＝0为起始弧端点；当s从x＝0沿实轴左侧趋于0时，记x＝0为终止弧端点.设γ＝α＋iβ，0≤α≤1，则

由于本文在函数类｛｛0｝｝中求解奇异积分方程（5），因此由开口弧段端点Cauchy型积分的性质知，对于以f（s）∈｛0｝（γ＝α＋iβ，0≤α≤1）为密度函数的Cauchy型积分F（x）＝T［f（t）］，在x＝0附近，有

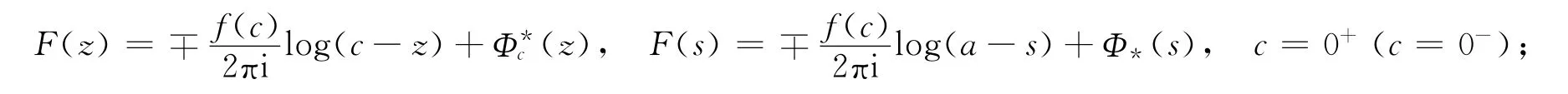
于是在x＝0附近，有

其中Φ＊c（s）在x＝0附近解析且属于函数类｛｛0｝｝.从而在x＝0附近，有

其中函数O＊（s）在x＝0附近全纯，且属于函数类｛｛0｝｝，当s→0时为0.

由式（23），（24），可得

由式（25），（26）及Φ＋（＋0）＝Φ＋（－0），有

可见，Fredholm积分方程（16）可解的必要条件即为积分方程（1）可解的必要条件.

假设x＝0是Riemann边值问题（4）的特异节点，在端点x＝0处，设γ＝α＋iβ，α＝0，则γ＝iβ.此时，式（23），（24）仍成立，并且

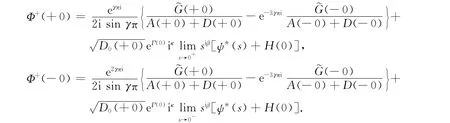
综上，可得本文的主要结果：

1）若κ≥0，则方程（1）可解的充要条件为式（18）成立，其解为式（22），其中F（x）由式（19）给出；

2）若κ＜0，则须添加可解条件（17），此时方程（1）可解的充要条件为式（20）成立，方程的唯一解为式（22），其中F（x）由式（21）给出.

［1］Duduchava R V.Integral Operators of Convolution Type with Discontinuous Coefficients［J］.Math Nachr，1977，79：75－98.

［2］LU Jian－ke.On Methods of Solution of Singular Integular Integral Equations with Convolution［J］.China Ann of Math，1987，8B（1）：97－108.

［3］MA Dao－wei.The Solution to Convolution Type Integral Equations with Singular Operator［D］.Wuhan：Wuhan University，1985.（马道玮.含有奇异积分算子的卷积型方程的解法 ［D］.武汉：武汉大学，1985.）

［4］SHEN Yong－xiang.A Kind of Integral Equation with both Two Convolution Kernels and Dual Type Property［J］.Ann of Math：Ser A，1991，12（1）：57－64.（沈永祥.一类含二个卷积核的对偶型奇异积分方程 ［J］.数学年刊：A辑，1991，12（1）：57－64.）

［5］LU Jian－ke，SHEN Yong－xiang.Singular Integral Equations Containing both Cauthy and Convolution Kernel in｛α，β｝［J］.Ann of Math：Ser A，1992，13（6）：672－680.（路见可，沈永祥.｛α，β｝类中含Cauchy核和卷积核的奇异积分方程 ［J］.数学年刊：A辑，1992，13（6）：672－680.）

［6］SHEN Yong－xiang.Some Kinds of Singular Integral Equations of Hilbert Kernel with Convolution ［J］.Acta Math Sci，1989，9（4）：421－426.

［7］SHEN Yong－xiang.Two Kinds of Singular Integral Equations with Convolution Kernel in the Non－normal Type Case［J］.Northestern Mathematical Journal，1989，5（1）：84－92.（沈永祥.两类具间断性质的含卷积核的奇异积分方程 ［J］.东北数学，1989，5（1）：84－92.）

［8］SUN Feng－qi.Solution of Completely Singular Integral－Differential Equation with Convolution Kernel［J］.Journal of Jilin University：Science Edition，2010，48（4）：605－608.（孙凤琪.含卷积核的完全奇异积分－微分方程的求解［J］.吉林大学学报：理学版，2010，48（4）：605－608.）

［9］SUN Feng－qi.Solution for a Class of RH－Boundary Value Problems in the Non－normal Type Case［J］.Journal of Jilin University：Science Edition，2007，45（3）：389－392.（孙凤琪.一类具有间断系数的RH边值问题求解 ［J］.吉林大学学报：理学版，2007，45（3）：389－392.）

［10］路见可，钟寿国.积分方程论 ［M］.北京：高等教育出版社，1988.

［11］SUN Feng－qi，SHEN Yong－xiang.Solution for a Class of Single－Value Branch Probloms［J］.Journal of Jilin University：Science Edition，2011，49（6）：1024－1028.（孙凤琪，沈永祥.一类单值化问题的求解 ［J］.吉林大学学报：理学版，2011，49（6）：1024－1028.）

［12］Cahov F D，Chersky U I.Equnations of Convolution Type［M］.Moscow：Moscow Press，1978.

［13］SUN Feng－qi，SHEN Yong－xiang.On Method of Solution for a Class of Dual Completing Singular Integral Equation with Two Convolution Kernels［J］.Journal of Northest Normal University：Natural Science Edition，2002，34（3）：14－20.（孙凤琪，沈永祥.关于一类含二个卷积核的对偶型完全奇异积分方程的求解 ［J］.东北师大学报：自然科学版，2002，34（3）：14－20.）