动态松弛方法中虚密度与时间步长的选择

陈新民，刘传奇，薛世峰

(1.中国石油大学储运与建筑工程学院，山东青岛 266580;2.胜利油田滨南采油厂，山东滨州 256600)

动态松弛法是将线性或非线性静力问题转化为动力问题，通过设置阻尼消耗能量，当位移收敛到平衡位置(即势能最小位置)时，迭代结束的显示求解方法［1］。Otter［2］在分析预应力混凝土核容器外壳时首次提出该方法;Cassell等［3］引入虚质量的概念;Underwood［4］对如何设定最有效的阻尼矩阵、质量矩阵进行了研究;David等［5］采用动态松弛法进行非线性分析，研究了超弹性结构;Michael［6］采用此方法进行了受拉结构的找形分析;Li等［7］应用动态松弛法求解可变形离散元中的节点运动方程;Rezaiee等［8］对虚质量与阻尼的具体算法进行了系统论述;李士军等［9］对Rayleigh阻尼参数取值进行了分析。当求解包含应力集中或其他局部网格加密的问题时，可通过设置虚密度，提高收敛速度［10］。对于虚密度影响收敛时步与计算结果的问题，相关文献研究较少。刘波等［11］从应力波传播角度讨论了不同单元如何设定密度与步长，但未能给出虚密度影响下时步设定的具体表达式。笔者以常应变三角形单元为例，探讨虚密度与时步的设定问题。

1 密度对收敛过程与结果的影响

从节点运动角度，可变形离散单元保持收敛的必要条件是单元Jacobi行列式恒大于零。如图1所示，在一个时步内，若节点k从原位置移动到k1位置，网格未出现畸变，保证在平衡位置附近振动，若移动到k2(Jacobi行列式为零)，k3(Jacobi行列式小于零)位置，则网格畸变，引起发散。

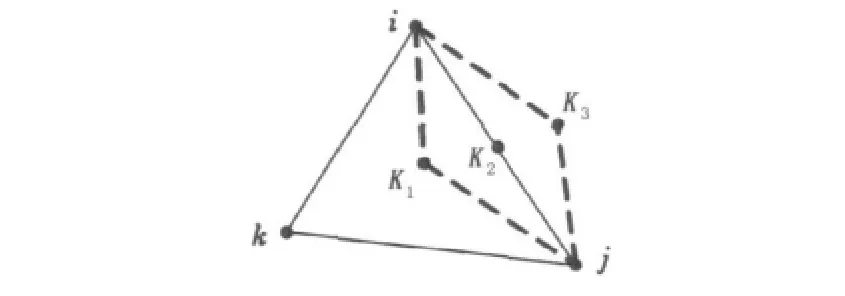
图1 单元节点位置示意图Fig.1 Schematic diagram of nodes position

遍历所有网格，初始状态顶点到对边最小距离记为Hmin，则计算收敛的必要条件是:Δt时间内，内含集中质量的节点位移小于Hmin。有

式中，Fext为k节点所受外力，N;mk为k节点集中质量(在三角形常应变单元中，mk=ρA/3)，kg;A为单元面积，m2;ρ为材料密度，kg/m3。

将mk带入式(1)中得

由式(2)可以明显看出，若单元密度增加，则收敛时间步长可相应增加。

从信息传递角度，迭代收敛的必要条件是当前计算速度必须大于信息传播的最大速度［11］，由此推导的最大收敛时间步长亦正比于密度的0.5次方。

针对密度变化影响最终平衡位置改变的问题，考虑单自由度含阻尼强迫振动，其运动方程为

其中

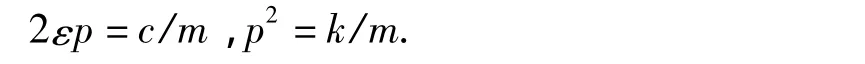
式中，ε为阻尼比;p为固有频率，rad/s;m为节点质量，kg;c为阻尼系数，N·s/m;k为弹簧刚度，N/m;F为所受外力，N。

根据杜哈梅积分公式［12］，初始条件为零的情况下，方程(3)的全解为

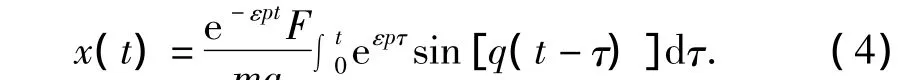
利用分部积分得到

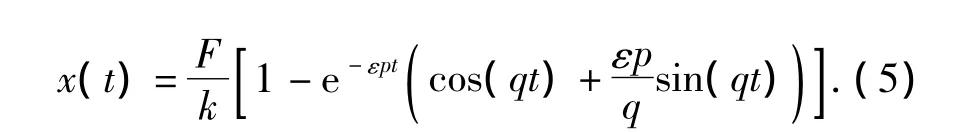
若按式(2)设定步长，将t=nΔt代入式(5)，则有

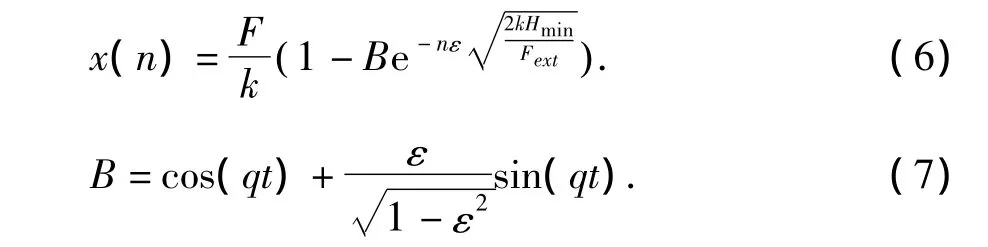
由式(6)可以看出，x(n)与密度无关，即按最大收敛时步进行迭代，收敛速度相同。因而，加快收敛的核心是设定虚密度和步长，使不同单元拥有相同的收敛时步，并且步长尽可能接近最大收敛时步。

2 虚密度与步长设定方法

单元节点运动受弹簧作用力影响，偏离平衡位置位移越大，所受弹簧力越大。弹簧力影响节点加速度，导致节点速度发生变化，单个时步的位移受到影响，反过来，影响下一时步的弹簧力。各因素影响关系如图2所示。

图2 迭代参数相互影响示意图Fig.2 Schematic diagram of iterative parameters mutual influence

图中，aij、vij、sij分别表示第 i步 j节点的加速度、速度、位移。假设j节点的最大收敛时间步长为Δtj，则有

采用三次迭代后，节点速度至少衰减为初速度一半的标准，确定时间步长，即:v3j≤0.5v1j，带入各自表达式，取等号进行方程运算，则有

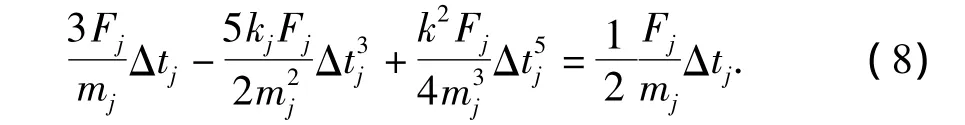
此方程为一元五次方程，共有5个不同的解，分别为

整个过程中未考虑阻尼影响，计算最大收敛时步需添加阻尼影响系数c，则j节点最大收敛时步为

式中，ρj为所设虚密度，kg/m3;Aj为单元面积，m2;k为弹簧刚度，N/m;c0为比例系数。

系统的收敛时步为ΔT=min{Δtj}，在实际应用中，首先计算最小单元面积，记为Amin，假定其密度，将单元j的密度设定为

此时，各单元收敛时步相同，再按照

设定步长，其中c0通过反复试算，取为0.45。

3 编程验证

基于可变形离散单元法进行编程验证。以平面受拉薄板为例，验证理论推导结论以及虚密度设定方案的有效性。计算模型如图3所示，由于薄板受集中力作用，采用不均匀网格(图3(b))。原来连续的节点分裂为夹有弹簧的两个角点，图中每个网格线间均有一对弹簧，方向分别为界面法向与切向。

为减弱由弹簧变形引起的位移不连续，将弹簧刚度设为单元弹性模量的50倍［7］，阻尼采用局部阻尼系数0.8［13］，弹性模量为20 GPa，泊松比为 0.2，密度为1.8×103kg/m3，弹簧刚度为1 000 GPa，阻尼系数为0.8。

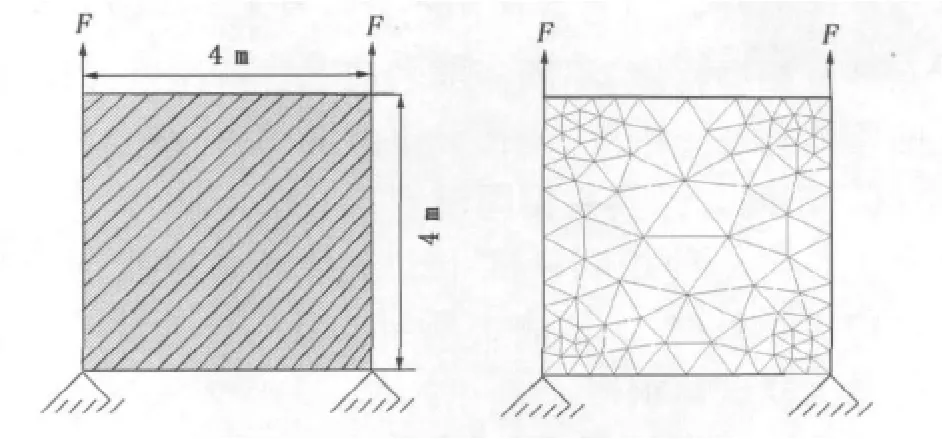
图3 计算模型示意图Fig.3 Schematic diagram of calculation model

采用C++语言编写可变形离散元程序。计算过程为:单元与单元之间通过弹簧相连，根据单元节点的相对位移计算弹簧作用力，采用高斯定理和Wilkins的大变形［14］有限差分法计算单元变形力，采用局部无黏性阻尼计算阻尼力，按照动态松弛法不平衡力—加速度—速度—位移—不平衡力的顺序进行迭代，当不平衡力数值小于预定值时，迭代完成。需要指出，速度与位移的求解是按照中心差分格式进行的。

图4为可变形离散元法和有限元软件ANSYS的计算结果，Y向最大位移分别为4.6×10－7m和4.7×10－7m，两种结果的相对误差为2.1%。通过改变单元密度进行计算，结果并未发生变化。

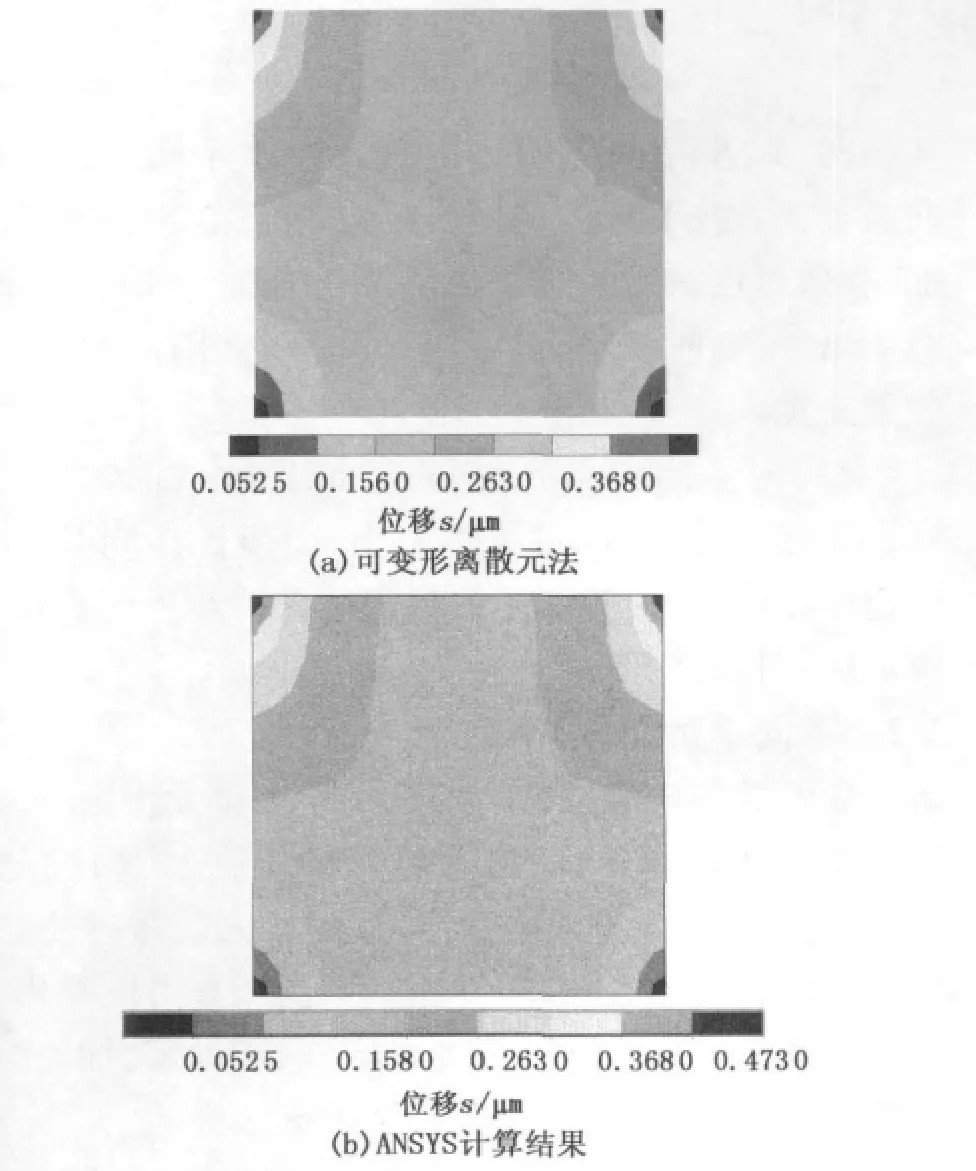
图4 可变形离散元法和ANSYS软件的计算结果Fig.4 Computed result of deformable discrete element method and ANSYS software

选取顶部左节点的内力作为参照，分别对各单元具有相同密度、不同密度的情况进行讨论，以验证推导结论及虚密度、步长设定方案的有效性。

3.1 不同单元具有相同密度

对比3种相同密度下的最大收敛时步与公式(11)的估计时步，如表1所示。其中最大收敛时步通过反复试算求得。

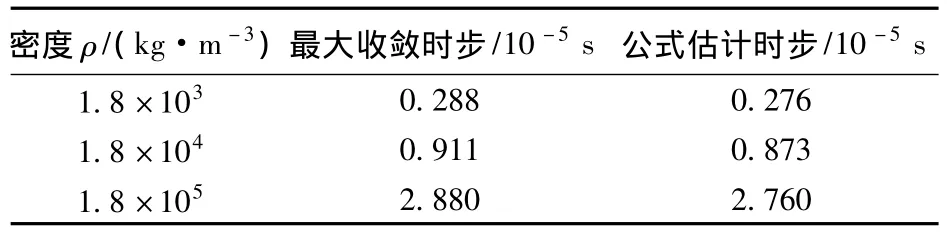
表1 收敛时步与估计时步对照Table 1 Comparison of convergence and estimated time step

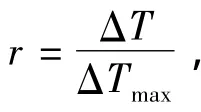
(1)密度相同(1.8×103kg/m3)、时步不同时，收敛曲线如图5(a)所示。由图5(a)可以看出，时步增加，收敛速度加快，这是由于密度不变，最大收敛时步不变，若时步增加，则时步比增加，增大了收敛速度。

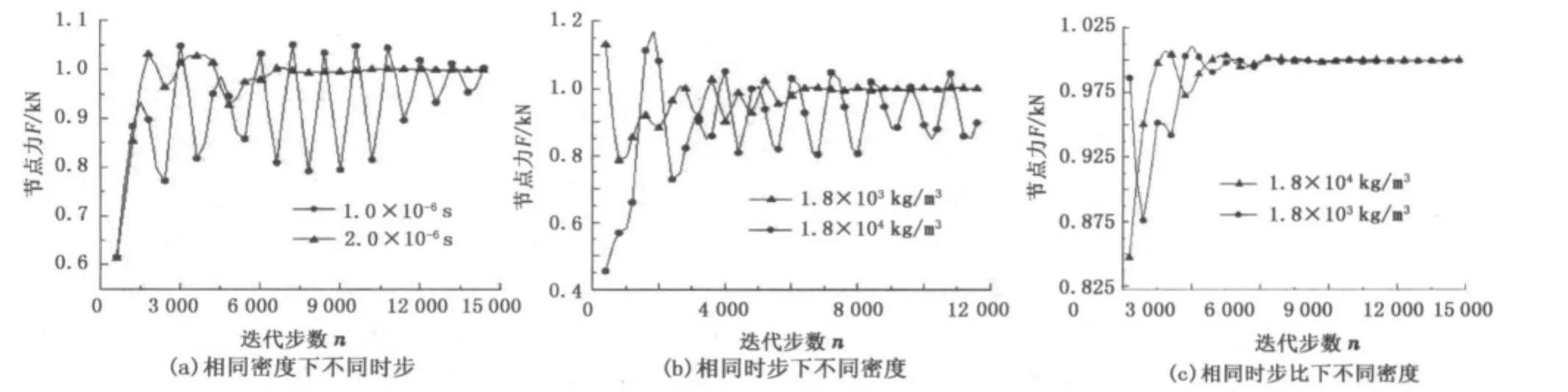
图5 相同密度下不同时步对照收敛曲线Fig.5 Comparison of convergence curve in different time step under same density

(2)时步相同(2.0×10－6s)，密度不同时，收敛曲线如图5(b)所示。由图5(b)可以看出，密度增加，收敛速度减缓。这是由于密度增加，则最大收敛时步增加，而时步恒定，则时步比减小，因而放缓了收敛速度。

(3)时步比均为1，密度不同时，收敛曲线如图5(c)所示。由图5(c)可以看出，时步比相同时，迭代速度相差不大，验证了按最大收敛时步进行迭代，收敛速度相同的结论。

3.2 不同单元具有不同密度

虚密度加速收敛的核心在于不同单元设定不同的密度，按照公式(10)进行密度设定，公式(11)进行时步设定，对比真实密度下按照最大收敛时步进行迭代的收敛曲线，如图6所示。由图6可以看出，按照本文所述方法进行密度设定，时步设定，加速收敛效果十分明显，验证了此方法的有效性。

图6 真实密度与虚密度对照收敛曲线Fig.6 Comparison of convergence curve in actual density and fictitious density

4 结论

(1)虚密度增大，可增大收敛时步。

(2)收敛速度与时步比有关，时步比越大，收敛速度越快。

(3)虚密度加速收敛的核心在于不同单元设置不同密度，使得不同单元拥有相同的最大收敛时步，按照所提出的密度、时步设定方案进行参数设定，加速收敛效果很明显。

［1］ TONG P.An adaptive dynamic relaxation method for static problems［J］.Computational Mechanics，1986(1):127-140.

［2］ OTTER J R H.Computations for prestressed concrete reactor pressure vessels using dynamic relaxation［J］.Nuclear Structural Engineering，1965，1(1):61-75.

［3］ CASSELL A C，KINSEY P J，SEFTON D J.Cylindrical shell analysis by dynamic relaxation［J］.ICE Proceedings，1968，39(1):75-84.

［4］ UNDERWOOD P.Dynamic relaxation［R］.Lockheed Report LMSC-D678265，1979.

［5］ DAVID R Oakley，NORMAN F Knight Jr.Adaptive dynamic relaxation algorithm for non-linear hyperelastic structures(Ⅰ):formulation［J］.Computer Methods in Applied Mechanics and Engineering，1995，126(1/2):67-89.

［6］ MICHAEL R Barnes.Form finding and analysis of tension structures by dynamic relaxation［J］.International Journal of Space Structures，1999，14(2):89-104.

［7］ LI Shi-hai，LIU Xiao-yu，LIU Tian-ping，et al.Continuum-based discrete element method and its applications［C］.Beijing:UK-China Summer School/International Symposium on DEM，2008:24-30.

［8］ REZAIEE-PAJAND M，ALAMATIAN J.The dynamic relaxation method using new formulation for fictitious mass and damping［J］.Structural Engineering and Mechanics，2010，34(1):109-133.

［9］ 李士军，马大为，朱孙科.动态松弛方法中Rayleigh阻尼参数取值分析［J］.计算力学学报，2010，27(1):169-172.LI Shi-jun，MA Da-wei，ZHU Sun-ke.Analysis of rayleigh danp parameters in dynamic relaxation method［J］.Chinese Journal of Computational Mechanics，2010，27(1):169-172.

［10］ 王泳嘉，邢纪波.离散单元法及其在岩土力学中的应用［M］.沈阳:东北工学院出版社，1991:46-47.

［11］ 刘波，韩彦辉.FLAC原理、实例与应用指南［M］.北京:人民交通出版社，2005:11-12.

［12］ 仇伟德.机械振动［M］.东营:石油大学出版社，2001:45-46.

［13］ PAPADRAKAKIS M.A method for the automatic evaluation of the dynamic relaxation parameters［J］.Computer Methods in Applied Mechanics and Engineering，1981，25(1):35-48.

［14］ LANRU Jing，SSTEPHANSSON O.Fundamentals of discrete element methods for rock engineering:theory and applications［M］.Amsterdam:Elsevier，2007.