降雨条件下土质边坡的稳定性分析

张 彪，何 翔，赵 青，包孟碟

(武汉工业学院土木工程与建筑学院，湖北武汉 430023)

滑坡灾害发生的原因多，成因复杂，由于局部暴雨或长时间降雨引发的滑坡灾害一直是分布最广泛、最频繁的滑坡灾害，所以水对滑坡的作用非常重要。降雨入渗是随时间、空间变化十分敏感的动态变化过程［1］。降雨的入渗量取决于降雨强度、降雨历时、土体的入渗能力等诸多因素。当降雨强度小于土体的入渗能力时，实际入渗量取决于降雨强度，土体含水量的增幅随着降雨强度的增大而增大，最后趋于稳定;当降雨强度大于土体的入渗能力时，实际的入渗量由土体本身的入渗能力控制。降雨开始以后，土质边坡首先在饱和区逸出点以上附近出现暂态饱和区，随着降雨历时的延长，暂态饱和区范围不断沿坡面扩展、延伸，逐渐在整个坡面形成一个由暂态饱和区构成的“饱和壳”，并随着降雨过程的延续向边坡内部扩展，影响范围逐渐扩大，“饱和壳”也越来越厚。随着降雨不断入渗，坡体内的含水量增加，孔隙水压力增大，进而边坡的基质吸力降低，土体的抗剪强度降低，从而导致边坡的稳定性降低［2］。目前，国内外学者对降雨入渗影响下边坡稳定性进行了广泛研究。Gofar N等［3］对降雨条件下滑坡的瞬态渗流与边坡稳定性做了一系列研究。原华等［4］在上海地铁10号线的基础上，对降水对软黏土渗流特性影响进行了试验。刘汉东等［5］研究了滑坡体在降雨条件下的稳定性。但基本上都是在建立饱和土假设的基础上，而传统的饱和土渗流及稳定性分析方法无法准确描述降雨过程中滑坡体内暂态饱和区的动态变化及其对滑坡稳定性的影响规律。

本文拟从非饱和土的渗流和抗剪强度理论出发，运用ABAQUS有限元软件，研究降雨入渗作用下土质边坡的稳定性。

1 非饱和渗流边坡稳定性分析

1.1 非饱和土的抗剪强度

1977年，加拿大Saskatchewan大学的 Morgenstern和Fredlund教授建议用2个独立变量(σua)，(ua－uw)建立抗剪强度表达式。Fredlund认为，非饱和土的抗剪强度由3个部分组成，即有效凝聚力c'，净法向应力(σ－ua)引起的强度，基质吸力(ua－ uw)对强度的贡献等。1978 年，Fredlund［6－7］提出了非饱和土的抗剪强度公式，其中净法向应力引起的强度与有效内摩擦角φ有关，而基质吸力引起的强度与φb有关。

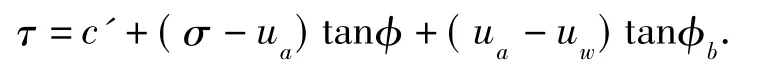
式中:τ为土体的抗剪强度;c'为有效黏聚力;σ为作用在破坏面上的总法向应力;ua为孔隙气压力，(σ－ua)为作用于破坏面上的净法向应力;uw为孔隙水压力，(ua－uw)为基质吸力;φ为有效内摩擦角，φb为随吸力变化的内摩擦角。

1.2 边坡稳定的强度折减法

强度折减系数概念最早由Ziekniewicz等［8］在土工弹塑性有限元数值分析中提出。抗剪强度折减系数定义为:在外荷载保持不变的情况下，边坡内土体所能提供的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比，称为强度储备安全系数.根据上述强度折减系数的定义，即可获得边坡的整体稳定安全系数折减后的抗剪强度参数可分别表达为:

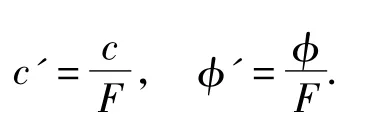
式中:c和φ为土体能够提供的抗剪强度，c'和φ'为维持平衡所需要的土体实际发挥的抗剪强度，F为抗剪强度折减系数或强度储备系数。

2 工程实例分析

2.1 工程概况

土地垇滑坡位于四川省屏山县新市镇，金沙江支流中都河出口段右岸，距坝址70.4 km。该滑坡顺坡分布长约320 m，横坡向宽340 m，平面面积约10×104m2，滑坡堆积体平均厚度约30 m，体积约300×104m3。滑坡发育于侏罗系沙溪庙组(J2s)地层中，岩性为紫红色薄层状泥岩、泥质粉砂岩夹细砂岩，基岩边坡呈缓倾外的顺向坡结构，从区内崩坡积物和阶地堆积物的分布情况分析，该滑坡系一崩坡堆积物和阶地堆积物的滑坡，滑坡组成物质主要为砂质粘土夹碎石和少量块石。

2.2 计算模型及参数选取

以边坡的实际地质条件为依据，利用ABAQUS有限元软件，建立滑坡数值模型，并划分网格，模型如图1所示，共计单元总数为47 410个，网格节点总计43 350个。在进行数值分析时，滑坡在降雨变化条件下，渗流的边界条件如下:① 流量边界:斜坡表面取降雨引起入渗的流量边界，当降雨强度大于坡面土体的入渗速度时，将土体的入渗速度值作为边界流量值;当降雨强度小于坡面土体的入渗速度时，将降雨强度值作为边界流量值。②两侧和底部渗流边界:模型底面和两侧为自由渗流边界，由于基岩的渗透性很弱，因此可认为是不透水边界。

根据工程类比，获得本次计算滑坡土体物理力学参数见表1。

图1 土地垇滑坡模型

表1 滑坡体物理力学参数

2.3 计算结果及分析

记录最近两年屏山县新市镇的降雨量，该地区月最大降雨量约为304 mm(2011年7月)、最小降雨量为0 mm(2011年12月和2012年1月)，日最大降雨量为94.7 mm(2012年8月19日);从总体趋势上看，该地区的降雨主要集中在每年的4—9月，约占全年降雨量的85%左右，最大降雨量出现在每年的7、8月份。鉴于此降雨量分布趋势，取日最大降雨量为94.7 mm(2012年8月19日)为研究前提，分析在此极限降雨条件下土地垇滑坡的稳定性，表2给出了不同工况及在该研究条件下采用强度折减法得到的滑坡体的安全系数。图2分别给出了在不同暴雨条件下土地垇滑坡滑坡体地下水位线的变化及水压力分布。

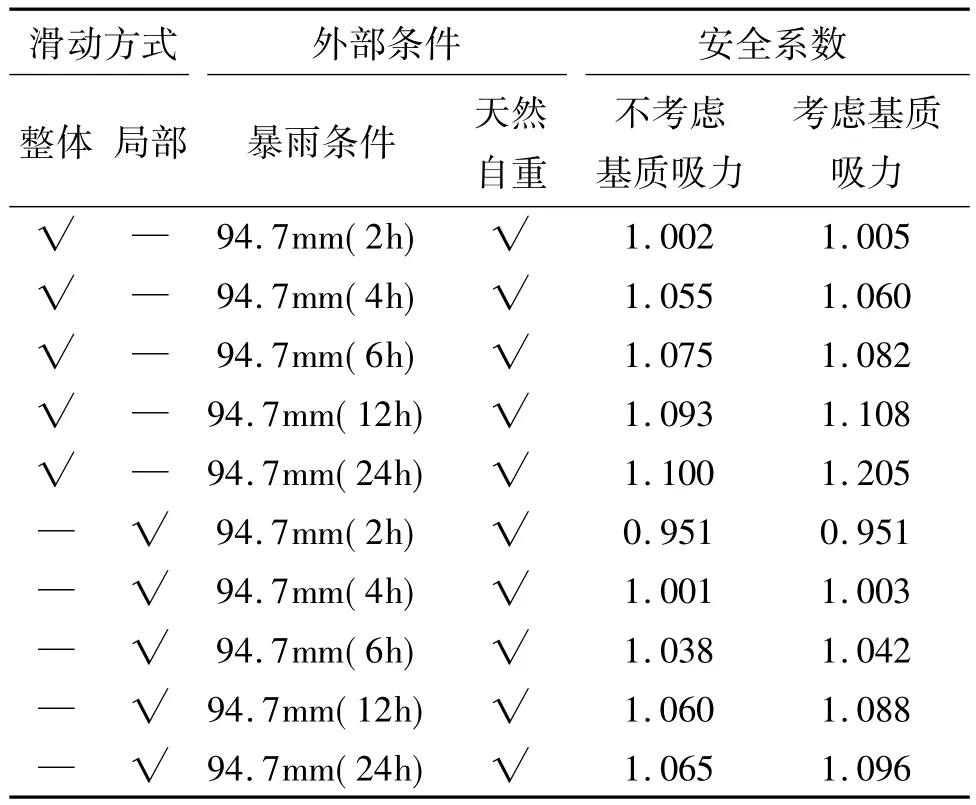
表2 暴雨条件下土地垇滑剖面安全系数表

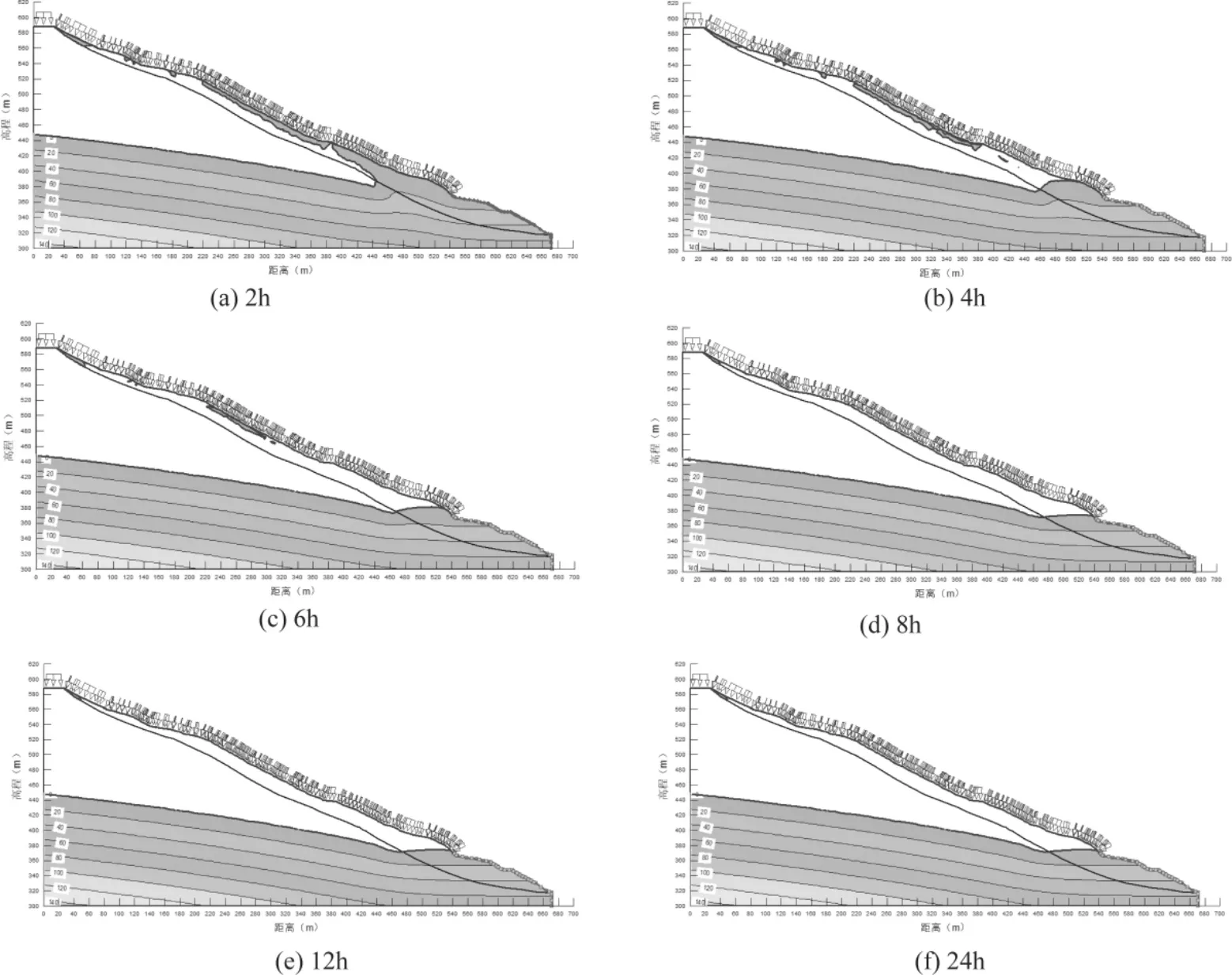
图2 在不同工况(a－f)条件下土地垇滑坡地下水位的变化及水压力分布

由表2可得，在不考虑基质吸力情况下的安全系数降低幅度比考虑基质吸力情况下的降低幅度要偏小，这是因为在暴雨工况下非饱和土的比例随着降雨持续在逐步减少，基质吸力的贡献因此也在逐渐减少。由图2可知:在2 h降雨量为94.7 mm(a图)时，在非饱和区域中，降雨开始以后，土质边坡首先在饱和区逸出点以上附近出现暂态饱和区，随着降雨历时的延长，暂态饱和区范围不断沿坡面扩展、延伸，沿着坡面中下部的暂态饱和区比较明显，并随着降雨过程的延续向边坡内部扩展，影响范围逐渐扩大，逐渐在坡面形成一个由暂态饱和区构成的“饱和壳”;由图2(b－f)中可以看出，随着降雨强度的降低，非饱和区的暂态饱和区域相应的减少，而且暂态饱和区的孔隙水压力对应降低，进而相对a图的基质吸力有所增加，增强了土体的抗剪强度，提高了边坡的稳定性。由图2可以看到，单位时间的降雨量越大，滑坡坡面的浸润线变化越明显。由表2可知:当暴雨降雨量为94.7 mm，滑坡的安全系数随着降雨强度的增加而减小，不考虑基质吸力的影响，当暴雨降雨时间为2 h滑坡的安全系数约为1.002，当暴雨降雨时间为24h滑坡的安全系数上升约为1.100;考虑基质吸力的影响，2 h滑坡的安全系数为 1.005，24 h 的安全系数为 1.205.

3 结论

运用非饱和渗流理论，研究边坡在不同降雨强度条件下坡体内的地下水位变化和水压力分布，以及非饱和区的暂态饱和区的形成机理和变化情况，进而影响基质吸力的变化，采用强度折减法对非饱和渗流的边坡稳定性进行分析，得出如下结论。

3.1 降雨入渗使得土质边坡首先在饱和区逸出点以上附近出现暂态饱和区，而且暂态饱和区的区域越来越大，饱和区的厚度也在增加;在不同的降雨强度条件下，暂态饱和区的区域和向边坡内部扩展的厚度也有所不同，降雨强度越大，暂态饱和区的区域和厚度也就越大，对应的降雨强度相对较小的时候，暂态饱和区的区域和厚度就就较小，对应的安全系数相对就越高，边坡就越相对安全。

3.2 在暴雨工况下，随着降雨时间的持续，单位时间的降雨量越大，滑坡体内的浸润线变化越明显，基质吸力对稳定性影响比较大;在考虑基质吸力情况下的安全系数降低幅度比不考虑基质吸力情况下的降低幅度要略微偏大。

3.3 在降雨量恒定情况下，滑坡的安全系数随着降雨强度的增加而减小;不考虑基质吸力的影响时，降雨强度从 94.7 mm/24 h 升至94.7 mm/2 h，边坡的安全系数从1.100降到1.002;考虑基质吸力的影响时，降雨强度从 94.7 mm/24 h升至 94.7 mm/2 h，边坡的安全系数从1.205 降到1.005。

3.4 在对边坡进行加固和治理时应充分重视边坡的排水，尽量使边坡处于较干燥的状态，以更利于边坡的长期稳定。

［1］徐光明，王国利.雨水入渗与膨胀性土边坡稳定性试验研究［J］.岩土工程学报，2006，28(2):270－273.

［2］田仕明，董羽蕙.边坡在降雨条件下的稳定性分析［J］.科学技术与工程，2010，10(24):6079－6083.

［3］Gofar N，Lee M L，Asof M.Transient seepage and slope stability analysis for rainfall induced landslide:A case study［J］.Malaysian Journal of Civil Engineering，2010(18):1 －13.

［4］原华，张建伟.降水对软黏土渗流特性影响的试验研究［J］.河南大学学报，2012，42(2):208－211.

［5］刘汉东，党灿，刘顺.滑坡体在降雨条件下的稳定性分析［J］.人民黄河，2012，34(3):65 －67.

［6］Alonso E，Gens A，Lioret A，et al.Effect of rain infiltration On the stability of slopes［J］.Unsaturated Soils，1995(1):241 －249.

［7］Fredlund D G，Morgenstern N R，Widger R A.The shear strength of unsaturated soils［J］.Canadian Geotechnical Journal，1978，15(3):313－321.

［8］Zienkiewz O C，Humphes C，Lewis R W.Associated and non－associated visco－plasticity in soil mechanics［J］.Geotechnique，1975，25(4):671－689.