影响磁导率测试的电磁检测探头设计因素分析
张玉华,李建增,孙慧贤,唐 卫
(1.军械工程学院,河北石家庄 050003;2.63853部队,吉林 白城 137000)
0 引言
火炮某些关键零部件,如顶针和轴类件易在发射过程中受强大的冲击力而损坏,因此,对其机械性能的控制很严格,其中,硬度是一项重要的衡量指标[1]。传统的机械压痕法通过在工件表面打点实现硬度检测,但具有破坏性,易造成零部件损坏,特别是有些零部件制作工艺复杂、加工成本高,不允许在其工作面上采用直接打点的方式进行硬度检测。此外,某些大型结构复杂的工件根本不可能放到传统的机械硬度试验机上进行检测,但在定型试验时要求必须检测其工件的硬度。由此可见,研究无损的便携式硬度测量仪对适应现代武器装备的维修和保障具有重要意义。
近年来,国内外开始研究利用电、磁、声等实现硬度测量的新方法,并取得了较好的效果。超声检测是利用装有压头的传感器杆的谐振频率增量来确定压头与被试材料的接触面积,以此来评价硬度[2],但由于测试中需加静载,仍会在工件表面产生小压痕。电磁硬度检测则是基于材料的磁特性或电磁感应原理建立起来硬度测试方法,可利用材料的磁导率、矫顽力、巴克豪森噪声等参数与硬度之间的相关性来实现检测[3~6],其中,磁导率法相对于其他方法,具有无接触、测量速度快、易实现便携式等优点,且探头可以不接触试件表面而实现硬度测量,这是一种真正意义上的无损检测。基于此,本文结合电磁感应原理,设计实现了一种以磁导率测试为基础的零部件硬度电磁检测探头,该探头包括1个检测线圈和1个参考线圈,通过建立电磁场—电路耦合仿真的有限元模型,分析了探头结构和尺寸、检测频率及后端电桥电路对检测性能的影响。
1 电磁检测原理与探头形式
检测原理如图1所示,当一空芯线圈通以正弦交流激磁电流后,线圈内部会产生一轴向的主磁场。如果将线圈被放置到被测试件表面,由电磁感应原理可知,试件中会感应出涡流,而涡流又会产生附加的次级磁场,这个次级磁场和主磁场之间的交互作用形成了线圈和试件的电磁耦合。如果待测参数发生改变,必然会改变线圈和被测工件之间的相互作用,最终表现为线圈阻抗或感应电压的变化。
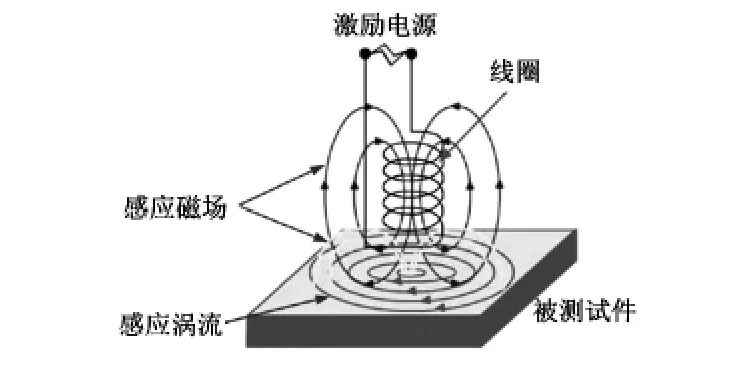
图1 电磁检测原理Fig 1 Principle of electromagnetic detection
电磁检测探头的结构形式多种多样,一般需要根据实际情况作设计。为了能有效检测出被测工件磁导率的变化,本文设计一种差分式检测探头如图2所示。探头包含检测线圈Z3和参考线圈Z4,检测中将检测线圈置于被测工件上方,而参考线圈则置于参考(标准)试件上方,两者通过电桥电路连接成差动输出。电桥另外2个元件Z1,Z2通常为电阻,其中1个可调,构成电桥中的2个桥臂。激励电压信号V加在电桥A,B两点之间,C,D两点之间的电压VOUT为电桥输出,即检测信号。
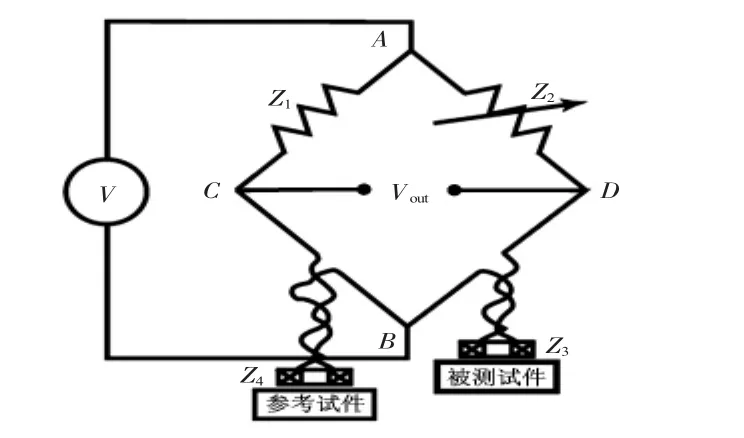
图2 差分检测探头与电桥结构Fig 2 Structure of differential detection probe and electric bridge
2 场—路耦合分析建模
由于检测探头后端有电桥电路存在,在进行仿真建模分析时,必须考虑外部电路的约束,因此,成为一个典型的场—路耦合问题的计算。这里,采用基于线圈磁链为耦合因子建立耦合仿真模型。
对于一个低频电磁场问题,可将求解区域Ω划分为涡流区Ωe和非涡流区Ω0两部分,采用A-φ位函数法求解,其中,A为矢量磁位,φ为标量电位。忽略位移电流,考虑解的唯一性问题,并入库仑规范Δ·A=0,则各部分的控制方程如下[7]:
在 Ωe内
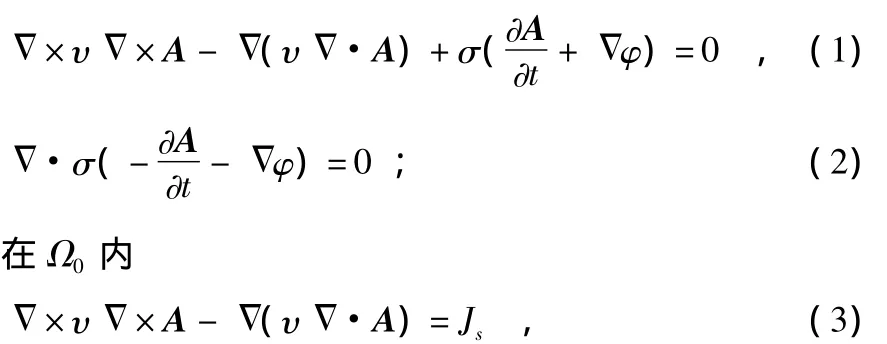
其中,Ω=Ωe∪Ω0,整个区域;Ωe为涡流区,其中包含导电媒质,电导率为σ,磁导率为μ;Ω0为非涡流区,μ0为空气磁导率,包含电流源Js(t),它是一个待求量,由线圈的外接电路决定。
既作为电磁场的场源又作为电路元件的线圈,其自身必须满足以下电路约束方程

式中 左边第一项为线圈直流电压,第二项为线圈的感应电势,ψ为线圈的磁链,右边为线圈端电压uc。R0为线圈的直流电阻,ic为线圈中流过的电流

其中,ns为线圈匝密度。根据法拉第定律,将线圈磁链ψ为矢量磁位A的函数[8]

其中,Ωc为线圈体积。上述式(1)~式(6)一起构成了电磁场—电路耦合分析模型,采用有限元法对具体问题进行数值求解。在建立实体模型之后必须对其进行空间离散化处理,这是有限元分析非常重要的一步。这里为了保证好的求解精度,导体、线圈及导体和线圈附近空气区域均采用六面体单元并增加划分密度,特别是在导体内部的集肤区域和线圈底部的空气隙,磁场的变化剧烈,网格划分最密。
3 关键设计因素分析
3.1 线圈尺寸
由第2节分析可知,线圈与被测工件发生电磁耦合作用,其结构尺寸对检测性能有直接影响。建立对应的有限元模型,仿真分析线圈的半径和高度对检测灵敏度的影响。
1)线圈半径
模型参数为:线圈的匝密度保持不变,高3.0 mm,内半径r1从1.25 mm增加到11.25 mm,外半径r2从2.75 mm增加到 18.75 mm,平均半径r=(r1+r2)/2,提离l1=0.5 mm,检测频率f=1 kHz。被测工件为长和宽均为40r2,厚均为5.0 mm,电导率 σ =5.0×106S/m,其相对磁导率 μr分别取200和210。将由磁导率变化引起的线圈阻抗的相对变化率定义为线圈的检测灵敏度,线圈检测灵敏度与平均半径r的关系如图3所示。
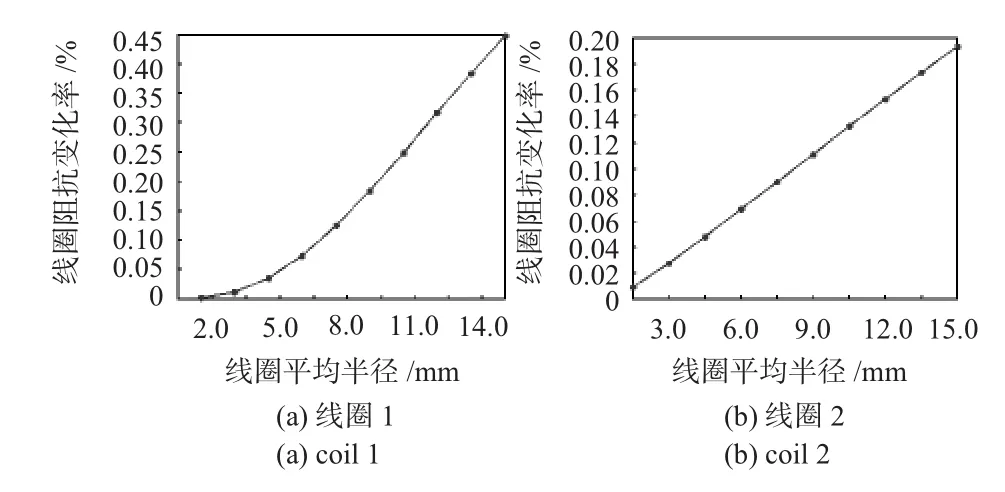
图3 线圈检测灵敏度随其半径的变化曲线Fig 3 Curve of detection sensitivity change with radius of coil
由图3可知,线圈半径增大,有利于检测灵敏度的提高。主要原因是线圈半径增大,则检测面积增大,线圈探头和被测工件之间的电磁耦合作用进一步增强。如果此时被测工件的磁导率发生变化,对线圈阻抗产生的反射作用更大,因此,灵敏度得到提高。
2)线圈高度
线圈内外半径保持不变,高h从 2.0 mm增加到12.0 mm,得到检测灵敏度与线圈高h的关系曲线,如图4所示。
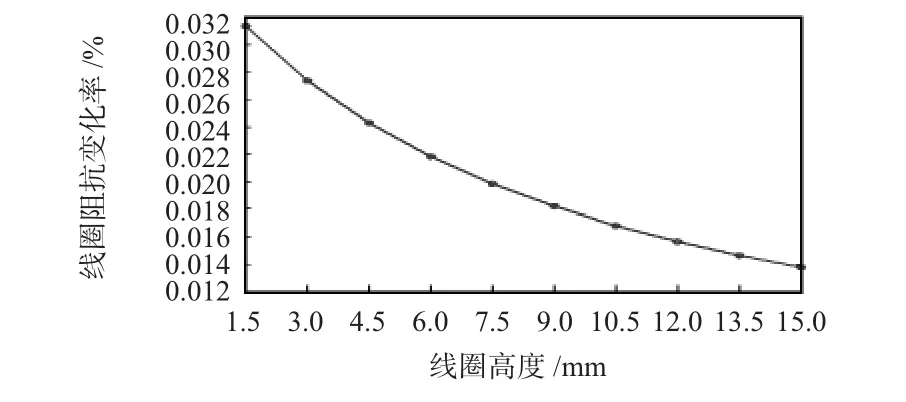
图4 线圈检测灵敏度随其高度的变化曲线Fig 4 Curve of detection sensitivity change with height of coil
从图中可以看出:随着线圈高度h增大,检测灵敏度的幅值单调减小。产生这种结果是因为在线圈内、外径不变的情况下,随着高度的减小,线圈磁场的聚集性越好,在靠近线圈附近磁场更强,从而使导体内涡流密度增大。因此,减小线圈高度有利于提高检测灵敏度。
3.2 线圈结构
在实际检测中,探头如果正处于被测工件边缘处,微弱的有用信号会被边界产生的强干扰所淹没。因此,必须在线圈结构上加以调整,降低边缘干扰。为解决这一问题,给线圈加一个倒“E”型磁芯,如图5所示,对比空芯线圈和加磁芯的线圈磁场分布图,如图6所示。
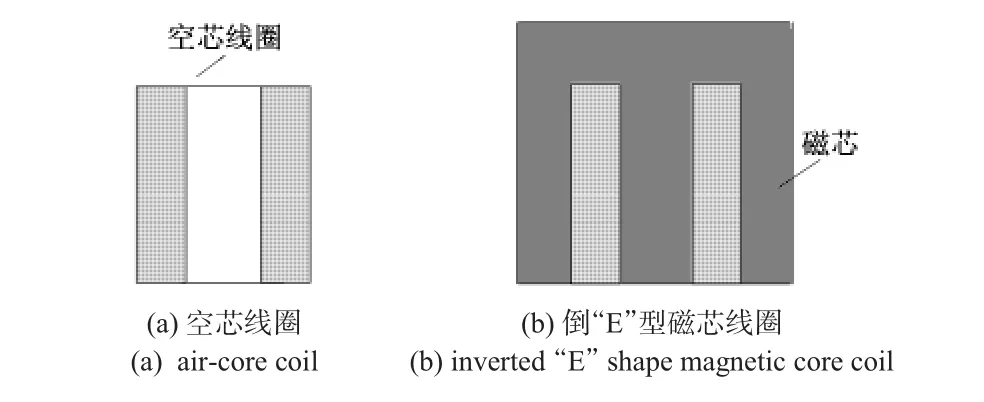
图5 线圈结构Fig 5 Structure of coils
从图中可以清晰地看到:空芯线圈产生的空间电磁场的分布要比磁芯线圈的大,而有磁芯的线圈,由于磁芯具有导磁特性,其磁场明显被汇聚在整个磁体的范围内,这就会导致在被测工件上感应出来的涡流分布也汇聚在磁芯线圈下方的区域内,而且感应场的强度值也比空芯线圈时增大。这说明在边缘部位检测时,由于磁芯线圈产生的涡流分布范围比空芯线圈产生的涡流分布范围要小的多,因而,边缘效应就会得到有效的减少或消除。同时相同的检测区域内的感应涡流密度,磁芯线圈的也大,这十分有利于提高检测灵敏度。
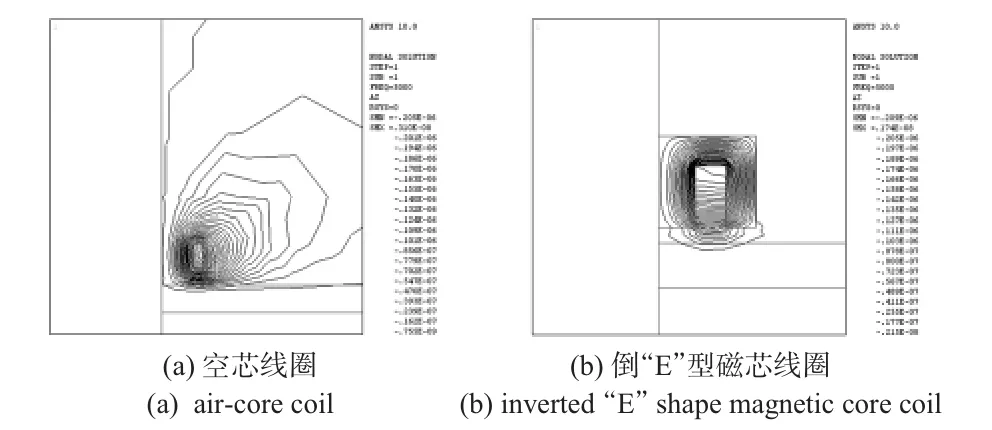
图6 空芯线圈和磁芯线圈的磁力线分布Fig 6 Distribution of magnetic line of force of air-core coil and magnetic core coil
3.3 检测频率
对于被测工件来讲,线圈中所加电流的频率直接影响感应电磁场在工件内部的渗透深度,从而影响检测性能。线圈和被测工件尺寸参数同3.2节,当线圈中通以频率f为100~5000 Hz变化的电流,设被测工件的磁导率有±10%变化,计算得到线圈电阻和电抗变化率随频率的变化曲线如图7所示。从图中可以看出:增大激励频率,可以增加线圈阻抗的变化率,即提高了检测灵敏度。但根据集肤效应,频率增大,导致电磁场渗透深度变浅,意味着可实现有效检测的深度范围缩小。如果要增加被测深度,则频率不宜过高,须折中选取。
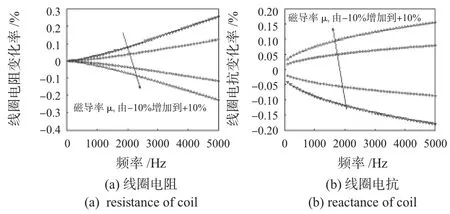
图7 线圈检测灵敏度随检测频率的变化曲线Fig 7 Curve of detection sensitivity change with detection frequency
3.4 检测桥路
电桥电路的基本原理是让基准信号在电路中自动平衡抵消,只保留并输出信号变化量。这里用磁导率变化引起的桥路输出电压的相对变化量来表示桥路的检测灵敏度。从理论上来讲,如果电桥电路处于平衡状态,则其检测灵敏度为∞,但实际中这一点不可能做到,主要是由于在实际绕制检测线圈和参考线圈时,两者的电气参数不可能做到完全一致。因此,研究在不平衡状态下,电桥电路的检测灵敏度更具有实际意义。
检测线圈和参考线圈的尺寸参数同3.2节,两者因为匝数不同导致电阻和电感不一致,分别针对2组不平衡状态进行仿真分析。被测工件和参考工件的几何尺寸和电导率均一致,两者的磁导率有5%的差别。计算得到电桥电路的检测灵敏度如图8所示。与图7对比可以得出如下结论:1)电桥电路对线圈阻抗的变化具有很好的放大作用;2)利用电桥电路可以大大提高检测灵敏度;3)电桥电路的灵敏度受桥路不平衡的影响大。对比图中2种不平衡状态下的检测灵敏度曲线可以发现,电桥不平衡程度越小,其灵敏度越高,所以,实际中应尽量降低电桥的不平衡程度。
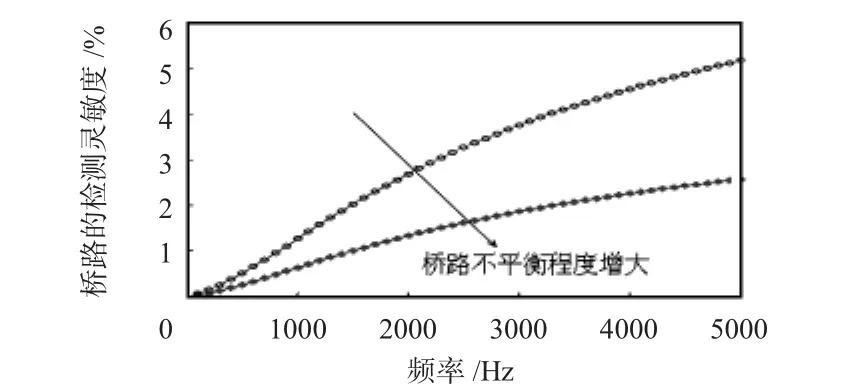
图8 电桥电路对检测灵敏度的影响Fig 8 Effect of electric bridge circuit on detection sensitivity
4 结论
1)设计了一种基于磁导率测试的硬度电磁检测探头。该探头包括一个检测线圈和一个参考线圈,并采用电桥电路实现差分式输出。
2)建立了电磁场—电路耦合分析模型,并采用有限元法求解。分析了探头结构和尺寸对检测灵敏度影响,结果表明:增大线圈半径、减小高度,有利于提高检测灵敏度。此外,给线圈加倒“E”型的磁芯,可以消除边缘干扰,同时提高检测灵敏度。
3)分析表明:增大检测频率可以提高检测灵敏度,但有效检测的深度范围缩小。
4)电桥电路可显著提高检测灵敏度,但电桥不平衡程度增大会降低灵敏度,所以,实际检测中应尽量保证检测线圈和参考线圈参数的一致性。
[1] 李家伟,陈积懋.无损检测手册[M].北京:机械工业出版社,2002.
[2] 成善宝,姚 进,蔡 鹏.超声波检测技术在硬度测量中的应用[J].中国测试技术,2004(1):11 -13.
[3] 贾昌磊,田 明,王庆龙.铁磁材料硬度无损检测方法研究[J].长春理工大学学报:自然科学版,2009,32(2):217-219.
[4] Kikuchi H,Onuki T,Kamada Y,et al.Initial permeability and vickers hardness of thermally aged FeCu alloy[J].Journal of Magnetism and Magnetic Materials,2007,310:2886 -2888.
[5] Bida G V,Nesterova V.Magnetic inspection of the hardness of cast-iron milling rolls[J].Russian Journal of Nondestructive Testing,2008,44(5):303 -308.
[6] 李 强,缪龙秀,王润志,等.利用巴克豪森噪声无损检测铁磁材料硬度试验研究[J].北方交通大学学报,2000,24(1):80-82.
[7] Biro O,Preis K.On the use of the magnetic vector potential in the finite element analysis of three-dimensional eddy currents[J].IEEE Transactions on Magnetics,1989,25(4):3145 -3159.
[8] Fu W N,Ho S L.Parameter extraction of eddy-current magnetic field-circuit coupled problems using matrix analysis method[J].IEEE Transaction on Magnetics,2008,18(22):1 -7.

