基于电致发光影像的太阳能电池瑕疵检测

李冠楠，谭庆昌*，张 阔，张宇鹏

(1.吉林大学 机械科学与工程学院，吉林 长春 130025;2.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

1 引 言

近年来，由于能源的不断枯竭以及全球暖化问题的日益严重，促使各国都在不断地寻找新能源，且考虑到地域限制、安全性等因素，现阶段较可行的下一代替代能源便是太阳能。太阳能电池是获取太阳能的最主要的光电组件，目前全球所生产的太阳能电池90%以上使用结晶硅，只有约10%使用薄膜技术。结晶硅依照制造材质不同，又可分为单晶硅、多晶硅与非晶硅，现今消费市场的应用大多使用多晶硅，主要是因为多晶硅制程简单且无需封装，所以价格较为便宜。在太阳能电池的制造过程中［1］，常因为疏失造成太阳能芯片表面刮伤、污点以及裂痕等瑕疵产生，如果忽视这些瑕疵，会造成太阳能电池的工作效率降低，甚至丧失储存电量的功能。因此，太阳能电池的制程检测是必要的。

随着太阳能电池产业的兴起，太阳能芯片/电池的瑕疵检测技术也得到了发展。2004年，Fu等［2］使用高斯-拉普拉斯滤波器找出单晶太阳能芯片表面裂痕的边缘，进而使用形态学滤除噪声并填补瑕疵。在检测技术上首先使用图像强化方法凸显裂痕的轮廓，接着利用该轮廓的几何特征及条件进行辨识。蔡欣儒［3］在2007年利用亚像素边界检测、霍夫变换和最小平方误差法来检测单晶太阳能芯片的边缘，并利用侦测到的边缘来判定是否有破损瑕疵。同年，陈心怡［4］针对不同类型的太阳能芯片影像，发展出不同的瑕疵检测技术。对具有均匀表面的太阳能芯片，以多选择性阈值检测瑕疵。对具有规律性纹理表面的太阳能芯片，则事先训练无瑕疵影像中10 种不同的纹理做为比对，以此检测模版区块内的瑕疵。

上述研究大多局限于单晶太阳能芯片的瑕疵检测，且假设裂痕在影像中有显著的灰度差异。多晶太阳能芯片则不能使用这些方法进行检测，主要是因为多晶太阳能芯片表面晶格分布很复杂，且瑕庛与正常晶格的轮廓都呈现细长线条形状，如果使用该方法进行检测，则会将瑕疵与正常晶格边缘同时检测出来，而造成检测误判。由于多晶太阳能芯片的表面瑕疵无法由肉眼或一般CCD 摄影察觉，因此可以运用电致发光(EL)影像技术［5-6］来凸显瑕疵。在EL 影像中，瑕疵具有条状或线状特性，而正常的随机晶格背景也会被凸显出来，使得自动瑕疵检测的困难加大。为此，本文提出了一种基于模糊C 均值(FCM)聚类法［7］的EL 影像瑕疵检测方法。首先，根据多晶太阳能芯片EL 影像的样本特性，对传统FCM 聚类法进行改进。其次，提取经过图像处理的正常影像样本的特征，并应用这些样本特征进行训练，即对正常样本进行分群。最后，根据训练结果完成多晶太阳能芯片的瑕疵检测。

2 改进的FCM 聚类分群方法

本研究旨在提高针对多群组未知数据进行辨识与分群的辨识准确率，以传统FCM 聚类分群法为基础方法，加入本研究的衡量标准与分群方法进行数据辨识与分群。由于具有二维特征的数据可以用绘图的方法将结果显示出来，因此本节仅以此类数据为例进行说明。

2.1 传统FCM 分群法

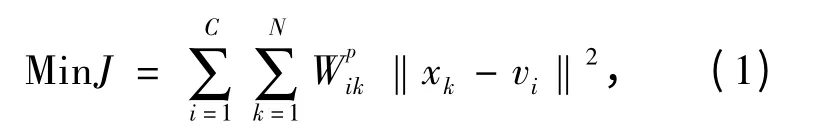
其中，C 代表分群数，N 为总样本数，xk为第k 个样本。参数p 是具有加权性质的指数，即取决于主观意识的模糊程度，也就是说p 值越大，模糊程度越大。在本研究中，使用的权重权数为p=2。

其中dik=‖xk－vi‖。各群中心点会因重新计算的权重的改变而跟着更新，计算方法如下:

通过迭代，当目标函数J 达最小值或收敛为一稳定值时，即求得各群中心点vi与最终分群结果并停止计算。

2.2 传统FCM 分群法的局限性

从传统FCM 的模型来看，虽然可以用于对任意群数的数据进行分群，但当样本的群数过多时，通过上述的迭代求最小值的方法对样本进行分类，就会使目标函数陷入局部的最小值，导致产生错误的分群结果。

如图1(a)所示的样本，从数据的分布情况看，应该将其分成20 群，但如果用传统FCM 分群法一次将其分成20 组，结果得到的20 个群的中心位置如图1(c)中实心点所示，从图中可以明显地看出分群效果不好，传统FCM 分群法并没有准确地找到每个群的中心。

图1 传统FCM 聚类法分群结果。(a)多群组;(b)疏密程度不同;(c)圆形与非圆形分布。Fig.1 Results of conventional FCM clustering method.(a)Multiple clusters.(b)Different level of density.(c)Circular and non-circular.

由于传统FCM 分群算法主要是利用样本点至中心点距离dik=‖xk－vi‖计算方式进行不断的演算修正，因此适合在数据结构密度相当、数据形态成近圆的情况下使用。对于两个数据形态拥有明显差异或者疏密程度明显不同的群集，以FCM 进行分群，其结果却不理想且有很明显的差异，如图1(b)和(c)所示。

2.3 针对多群数的改进FCM 分群法

一般认为，传统FCM 分群算法适合分较少群数的样本，因此首先利用传统FCM 分群算法将样本分为两群，通过均匀度的概念来衡量需要下一次分群的群组，即哪一群的均匀度差下一次就分哪一群，再用传统FCM 分群算法将均匀度差的那一群分成两群，以这两群替换原来的群组。之后，继续在剩下的所有群组中寻找均匀度最差的群组，并将其分成两群，直到达到所需群数为止，其演算过程如图2 所示。这种分群方法有助于充分利用传统的FCM 分群算法的特点，而且只需一个参数来控制分群结果，该参数即为所分群数。

图2 针对多群数样本的改进FCM 聚类法流程图Fig.2 Flow chart of improved FCM clustering method aiming at samples of multi-clusters

从样本特征值的意义来看，一般认为在同一群内如果两两样本的相关程度基本都一致，则该群的均匀性较好;如果两两样本的相关程度不一致，则均匀度较差。因此，可以用主成分分析方法中的协方差矩阵来定义同组样本的相关程度。

为了叙述方便，把测试样本写成如下形式:

首先，对样本做零平均值处理，即:

其次，计算样本的协方差矩阵K:

其中，A=［Δ x1Δ x2… Δ xc］。

最后，由协方差矩阵K 的特征值来计算群组的均匀度。令λ=［λ1λ2… λc］为协方差矩阵K 的c 个特征值，如果群组中样本的相关性不一致，则c 个特征值的标准差较大，否则这个标准差较小。由于各群组样本的疏密程度不完全相同，导致各群组的特征值不在同一数量级上，因此用协方差矩阵K 的特征值的标准差与均值的比值作为均匀性的衡量标准，即均匀度，其公式为:

2.4 针对样本分布形态的改进FCM 分群法

在使用上述改进FCM 分群算法进行分群时，每次用传统的FCM 分群算法把某个群组分为两群，经常会出现样本形态不是近圆形或疏密程度不均的现象。为了避免这种情况导致错误的分群结果，需要对每次分群时使用的传统FCM 分群算法进行改进。本文将式(5)的目标函数改为如下形式:

由于传统的FCM 并没有考虑到数据的分散程度，因此在本研究中加入了变异数因子，该变异数因子是每个样本点对各群中心点之变异程度，以加强同一群样本之间的紧密性(相关性):

同时，将传统FCM 算法中的dik=‖xk－ vi‖修改为:

当r 逐渐增加时，每个样本点至各群中心点距离的差距变大，便可达到加剧各群间差异性的目的。根据实验资料测试，本文采用r=3。总结起来，针对样本分布形态的改进FCM 算法演算流程如下:

(2)随机从原始数据中取出一笔数据作为初始质心位置vi;

(4)求得目标函数J;

(7)更新质心位置vi;

图3 改进FCM 聚类法分群结果。(a)多群组;(b)疏密程度不同;(c)圆形与非圆形分布。Fig.3 Results of improved FCM clustering method.(a)Multiple clusters.(b)Different level of density.(c)Circular and non-circular.

(8)重复(4)～(7)，当J 达最小值或收敛为一稳定值时，计算停止。

如图3 所示，使用改进FCM 聚类法对图1 数据进行分群，误判点的数目明显减少，对样本的辨识率得到了明显的提高。

3 特征提取

图4 形态学处理实验结果。(a)形态学处理前;(b)形态学处理后。Fig.4 Results of morphological processing.(a)Before morphological processing.(b)After morphological processing.

对于多晶太阳能芯片，金属手指断线(图5(a))、微裂痕(图5(b))和裂痕(图5(c))是最常出现的3 种瑕疵，这些瑕疵在随机晶格背景图案中呈现条状或带状特征。因此，根据Rainer Lienhart 等［8］提出的扩展Haar 特征，本文选取以下12 个特征用于边缘像素点的特征值提取，如图6 所示。

图6 的3 组特征，每组的后2 个特征是由该组前两个特征逆时针旋转45°得到的。在这3 组特征中，第1 组和第2 组是边缘特征，第3 组是线状特征。每个特征的特征值可用公式表示为

图5 太阳能芯片EL 影像瑕疵种类。(a)金属手指断线;(b)微裂痕;(c)裂痕。Fig.5 Defect types of solar cell in EL image.(a)Fingerinterruption.(b)Micro-crack.(c)Crack.

图6 本文所选用的12 种扩展Haar 特征Fig.6 12 extended Haar features proposed in the article

其中:Fj代表第j 种Haar 特征的特征值，ω1是第j个Haar 特征的权值，ω2是第j 个Haar 特征中黑色矩形的权值，R1代表第j 个Haar 特征中包含的所有像素点的灰度值之和，R2代表第j 个Haar 特征中黑色矩形块所包含的所有像素点的灰度值之和。前两组特征原型的权值比ω1∶ω2=1∶(－2)，第三组特征原型的权值比ω1∶ω2=1∶(－3)。

当固定Harr 块的大小时，用这12 个特征对影像中的边缘像素点进行特征值提取，即以该像素点为中心对Haar 块大小的区域内的所有像素点做如公式(10)的运算，对于每个边缘像素点就可以得到该样本的12 特征值。为了测量像素尺寸不同大小的瑕疵，可以取多种Haar 特征的尺寸，如果取r 种Haar 特征的尺寸，对于某一个像素点，就可以得到12 ×r 个特征值。

4 训练与测试

4.1 训练

本文在训练时，只采用正常边缘像素点的样本作为训练样本，这就要求要收集到几乎全部形式的正常样本。这种要求对于用肉眼判断的方式是很难做到的。本文采用以下方法:(1)通过观察首先收集得到一些不同形式的正常无瑕疵的EL 影像(如图7 所示)，共10 张，将这些影像上的每个边缘像素点作为一个样本，这些样本称作不完全正常样本;(2)用上述不完全原本进行训练，并对若干张正常影像进行测试，在测试结果中会出现很多误判点，这些误判点是将正常样本判成了瑕疵样本，原因在于训练样本中并不含有这些正常样本，因此再将这些误判点附近的影像(如图8 所示)加入到训练影像中，这样就得到了几乎全部形式的正常样本。

图7 不完全的无瑕疵太阳能芯片EL 影像(经过形态学处理)Fig.7 Incomplete EL image of defect-free solar cell (after morphological processing)

图8 误判的无瑕疵太阳能芯片EL 影像(经过形态学处理)Fig.8 Misjudged EL image of defect-free solar cell (after morphological processing)

用上述正常样本进行训练，即使用第二节改进的FCM 分群法将其分为n 个群集。对于每个测试样本，计算它到自身所属群的群中心的欧式距离

其中，xi为第i 个样本，i=1，2，…，n;vj为xi所在群的中心，j=1，2，…，n。

则每一群的阈值可定义为:

胃穿孔发病的原因具有较强的复杂性,其发病的原因也比较多,如胃溃疡、胃癌等,在传统的急性胃穿孔治疗中,主要采用开放式穿孔修复术。当前治疗急性胃穿孔最好的方式是外科手术治疗,此外应尽早实施手术。若患者就诊时已经超过12h且腹部感染情况较为严重[6]。出现中毒性休克、肠粘连、肠梗阻以及其他并发症的可能性明显提高,且相关的研究显示,对于急性胃穿孔患者,只要患者耐受,均可采用胃大部切除手术进行治疗。

4.2 测试

对于某个待测样本，根据公式(11)计算其到第j 个群中心的距离dj，如果该距离大于Tj，则这个样本不在该群中;如果该距离小于Tj，则这个样本在该群中。即:

如果测试样本不属于n 群中的任何一个群，就定义该样本是瑕疵样本;如果测试样本属于n群中的某个群，就定义它是一个正常样本。

5 实 验

实验时，使用一个直流电源向太阳能电池输出0.4～0.6 V 电压和6～20 mA/cm2电流;使用冷却的近红外光(λ=1.1～1.2 μm)CCD 相机在完全密不透光的环境下取像，无需任何外加光源。

从图6 各Haar 特征的样式可以看出，Group1和Group2 将Haar 块的宽w 平均分成了2 份，Group3 将Haar 块的宽w 平均分成了3 份。因此，为了使每个Haar 特征的每个区域(黑色区域或白色区域)都为整像素，Haar 块的宽w 必须是6 的整数倍。通过观察和实验分析，选择参数如下:

Haar 块大小:h=18，w=6，12，…，42;分群组数:30 组;阈值Tj中t 值:0.02。

图9 原始测试影像与测试结果。(a)～(h):原始瑕疵影像;(a')～(h'):瑕疵检测结果。Fig.9 Original testing images and testing results.(a)～(h):Original defect image.(a')～(h'):Defect detection result.

实验选用改进FCM 聚类法对正常样本进行分群，并用该训练结果对50 块太阳能芯片(20 块瑕疵+30 块正常)进行测试，测试的统计结果显示:20 块瑕疵样本中，有18 块被判为瑕疵，2 块被判为正常，误差为10%;30 块正常样本中，0 块被判为瑕疵，30 块被判为正常，误差为0。50 个样本的总辨识率高达96%，其中12 块的测试结果如图9 所示。

6 结 论

本文介绍的改进FCM 分群算法能够有效地解决多群数数据分类问题，明显提高分群辨识率。本研究在训练过程中只用到了正常样本，省去了收集瑕疵样本的复杂过程，给瑕疵检测带来了极大的方便。根据瑕疵的特点，本文选择大小适当的Haar 特征，使用改进FCM 分群法将训练样本分为30 组，阈值Tj中的t 选用0.02，可以有效地对太阳能电池EL 影像中的瑕疵进行检测，并能够近似地给出瑕疵的位置，有助于工厂进行自动化的太阳能电池的制造检测。

［1］Zhang M J，Li J D，Chen J S.Solar cell and production of polysilicon［J］.J.Mater.Metall.，2007，6(1):33-38.

［2］Fu Z，Zhao Y Z，Liu Y，et al.Solar cell crack inspection by image processing［C］// 2004 International Conference on Business of Electronic Product Reliability and Liability，New York:Cambridge University Press，2004:77-80.

［3］Tsai H J.The Scale Measurement and Defect Inspection for Printed Solar Cell［D］.Chungli:National Central University，2004.

［4］Chen S Y.Surface Defect Detection for Solar Cells［D］.Chungli:National Central University，2004.

［5］Fuyuki T，Kondo H，Yamazaki T，et al.Photographic surveying of minority carrier diffusion length in polycrystalline silicon solar cells by electroluminescence［J］.Appl.Phys.Lett.，2005，86(26):262108.

［6］Fuyuki T，Kitiyanan A.Photographic diagnosis of crystalline silicon solar cells utilizing electroluminescence［J］.Appl.Phys.A，2009，96(1):189-196.

［7］Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithm［M］.New York:Plenum Press，1981.

［8］Lienhart R，Maydt J.An extended set of Haar-like features for rapid object detection［C］// 2002 IEEE ICIP，New York:CRC Press，2002:900-903.